修订:20200313,边缘检测与拉普拉斯算子
文章目录
- Visual Features 图像特征
- 2. 边缘检测的一些方法(梯度sobel、Prewitt、Roberts、拉普拉斯算子)
- 2.1 边缘检测的一种思路:求微分
- 2.2 sobel
- 2.3各向同性的滤波器
- 2.4 最简单的各向同性微分算子——拉普拉斯算子
- LOG
- 传统高斯金字塔
- Sift算法中的多尺度金字塔
- 规范化
- 尺度的选择
- invariant 恒定性
- The descriptor should be also rotation invariant 旋转不变性
- 从单元中提取特征描述符
- SIFT检测示例
- Create Image Mosaic
- SVD
- 齐次与线性
Visual Features 图像特征

目标:寻找图片中的特殊的点
目的:通过这些点寻找到图片变换关系
可以得到:定位,三维重建,场景识别以及影像索引。localization,reconstruction,place recognition,place recognition
特征具有描述不变性(Descriptor Invariance)
- 即使尺度、方向变化了,依然可以重复检测到。 image differs in scale and orientation ,Detection Repeatability
SIFT特征提取方法:
更多方法:MATLAB图像处理-特征提取-形状特征 方法小结:https://blog.csdn.net/djfjkj52/article/details/104542436

SIFT尺度空间的建立过程:将原始影像与不同参数的高斯核做卷积,即可得到不同模糊程度的影像。当高斯核的σ变为原来的2倍时,对影像进行金字塔降采样。
关于金字塔采样:https://blog.csdn.net/djfjkj52/article/details/104433936


最大跨尺度是图像结构的固有尺度
如果平滑后的值已按比例归一化。
事实证明,只有高斯响应的导数可以归一化。
2. 边缘检测的一些方法(梯度sobel、Prewitt、Roberts、拉普拉斯算子)
https://www.w3cschool.cn/opencv/opencv-xzil2cu8.html
https://zhuanlan.zhihu.com/p/30994790
2.1 边缘检测的一种思路:求微分
对于一维函数f(x),其一阶微分的基本定义是差值:
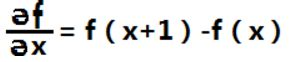
我们将二阶微分定义成如下差分:
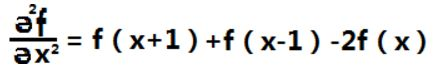
看边缘的灰度分布图以及将一二阶微分作用于边缘上:

可以看出:微分算子(尤其是二阶微分),对边缘图像非常敏感。
2.2 sobel
Sobel操作符
这是基于以下事实:在边缘区域中,像素强度显示“跳跃”或强度的高变化。得到强度的一阶导数,我们观察到边缘的特征是最大值,如图所示:下图(a)中灰度值的”跃升”表示边缘的存在.如果使用一阶微分求导我们可以更加清晰的看到边缘”跃升”的存在(这里显示为高峰值)图(b);
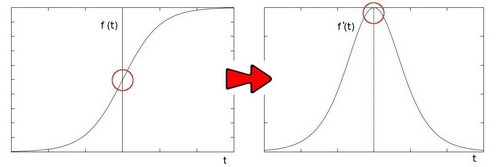
采取二阶导数会发生,二阶导数为零!因此,我们也可以使用此标准来尝试检测图像中的边缘。然而,请注意,零不仅会出现在边缘(它们实际上可以出现在其他无意义的位置); 这可以通过用’过滤’来解决。

2.3各向同性的滤波器
这种滤波器的响应与滤波器作用的图像的突变方向无关。也就是说,各向同性滤波器是旋转不变的,即将原图像旋转之后进行滤波处理,与先对图像滤波再旋转的结果应该是相同的。
2.4 最简单的各向同性微分算子——拉普拉斯算子
2.4.1 用途:
拉普拉斯算子——基于拉普拉斯变换的图像增强已成为图像锐化处理的基本工具。
在图像处理和计算机视觉中,拉普拉斯算子已经被用于诸如斑点检测:Blob detection和边缘检测等的各种任务。
2.4.2 数学定义:
在数学以及物理中,拉普拉斯算子或是拉普拉斯算符(英语:Laplace operator, Laplacian)是由欧几里得空间中的一个函数的梯度的散度给出的微分算子,通常写成 。
英文是 Laplace operator 或简称作 Laplacian。
性质
首先,拉普拉斯算子是最简单的各向同性微分算子,它具有旋转不变性。
一个二维图像函数f(x,y)的拉普拉斯变换是各向同性的二阶导数,定义为:
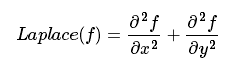
那么对于一个二维图像f(x,y),我们用如下方法去找到这个拉普拉斯算子:
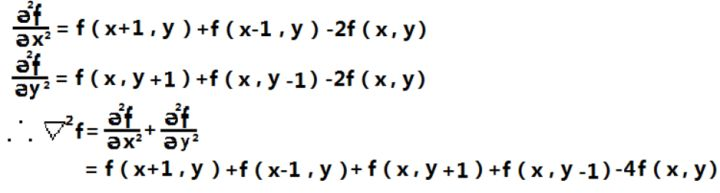
这个结果看起来太复杂,我们能不能用别的方式重新表达一下,如果我们以x,y 为坐标轴中心点,来重新表达这个算子,就可以是:
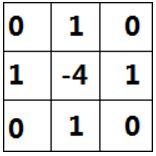
Laplace Operator 相关问题
- laplace 算子为何是 x 和 y 的二阶偏导的和。
这样可以同时响应 x,y 两个方向梯度的变化。通常来讲,边缘的特性是在同一点,只有一个边缘梯度方向。比如说是水平的,或者垂直的,或者 45 度这样的,这些情况都没有问题。但有一个极特殊情况,那就是 x,y 方向的二阶偏导是相互抵消的,导致边缘没有响应,或者响应变弱了。这种情况虽然极少,但确实是存在的。好在即使存在,也只可能是个别点,基本可以忽略。
- laplace 算子的优劣之处
由于 laplace 使用二阶偏导找过零点,那么对一些很小的灰度变化,也能灵敏的响应。但这也导致了其对噪声很敏感,尤其是孤立的噪声点特别强烈。因此,最好提前进行平滑处理,比如使用高斯滤波。高斯和拉普拉斯算子结合在一起,就是 LoG 算子.
由于 laplace 使用二阶偏导数,使其对应平缓的梯度变化不敏感,这是区别于一阶导数的地方。因此,如果不想检测出平缓的粗边缘,使用二阶导数更合适。
laplace 可以通过两侧的符号判断边缘灰度是增还是减,有一定的实际用途。
例程:
import cv2
import numpy as np
kernel_size = 3
scale = 1
delta = 0
ddepth = cv2.CV_16S
img = cv2.imread('test.jpg')
img = cv2.GaussianBlur(img,(3,3),0)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
gray_lap = cv2.Laplacian(gray,ddepth,ksize = kernel_size,scale = scale,delta = delta)
dst = cv2.convertScaleAbs(gray_lap)
cv2.imshow('laplaceOperater',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

LOG
由于 laplace 使用二阶偏导找过零点,那么对一些很小的灰度变化,也能灵敏的响应。但这也导致了其对噪声很敏感,尤其是孤立的噪声点特别强烈。因此,最好提前进行平滑处理,比如使用高斯滤波。高斯和拉普拉斯算子结合在一起,就是 LoG 算子.

如果函数按比例归一化,则我们可以获得具有此最大值的内在比例
可以归一化的函数是高斯函数的导数。
让我们以二阶导数为例。二维函数的二阶导数通常是矩阵,即Hessian。但是,如果我们追踪它,就会得到所谓的高斯拉普拉斯算子。
这是一个看起来像墨西哥帽的表面,它具有非常好的属性,它具有很好的属性,可以将其近似为两个高斯的差,并且可以检测类似斑点的特征
传统高斯金字塔
https://blog.csdn.net/piaoxuezhong/article/details/78114948
尺度空间 (Scale space)
尺度空间理论是由计算机视觉,图像处理和信号处理领域开发的多尺度信号表示的框架,其动力来自物理学和生物视觉。它是一种用于处理不同比例尺图像结构的正式理论,方法是将图像表示为单参数平滑图像族,比例空间表示法通过用于抑制精细比例结构的平滑核的大小进行参数化。 维基百科(英文)
传统的图像金字塔是通过降采样加平滑得到的。首先将原始图像作为最底层图像G0(第0层),利用高斯核函数对其进行卷积,然后对卷积后的图像进行下采样,得到上一层的图像G1(第1层),重复上面的卷积和下采样操作,反复迭代多次,便得到一个金字塔形的多层图像。自下而上每一层的像素数都不断减少,变得越来越粗糙,进行高斯平滑操作是为了降采样后的像素点能更好地代表原图像的像素点。

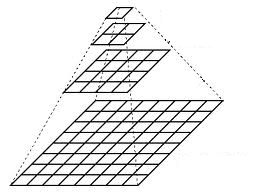
上图中,左边为高斯卷积核,右边为图像金字塔的形象说明,图像金字塔中所有图像来源于同一张原始图像,通过多次向下采样获得,直到达到某个终止条件。
常用的图像金字塔有两种:高斯金字塔和拉普拉斯金字塔。
高斯金字塔(Gaussian pyramid):
高斯金字塔的当前层图像就是对其前一层图像首先进行高斯低通滤波,然后再隔行和隔列降采样生成。前一层图像大小依次为当前层图像大小的4倍,多次向下采样得到的图像序列
拉普拉斯金字塔(Laplacian pyramid):
高斯金字塔的每一层图像减去上一层图像上采样+高斯卷积之后的图像,得到的差值图像即为拉普拉斯金字塔当前层图像。
Sift算法中的多尺度金字塔
Sift算法中提出的高斯金字塔不同于上面提到的传统金字塔结构,它是由很多组(Octave)构成,每组都包含若干层(Interval)。
差分金字塔与Difference of Gaussian(DOG)高斯函数的差分
差分金字塔,是在高斯金字塔的基础上构建起来的,DOG金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。

特别注意:传统金字塔与sift算法提到的金字塔,最最重要的区别在于多尺度与多分辨率的区分。传统金字塔的层与层之间的图像结构分辨率是不同的,sift算法中,同一组(octave)中的多层图像分辨率是相同的,只是高斯平滑时使用的参数不同,但这并不影响分辨率。
高斯差 (Difference of Gaussians)
https://www.cnblogs.com/raorao1994/p/9009945.html
说明在计算机视觉中,高斯差是一种将一个原始灰度图像的模糊图像从另一幅灰度图像进行增强的算法,通过DOG以降低模糊图像的模糊度。这个模糊图像是通过将原始灰度图像经过带有不同标准差的高斯核进行卷积得到的。用高斯核进行高斯模糊只能压制高频信息。从一幅图像中减去另一幅可以保持在两幅图像中所保持的频带中含有的空间信息。 维基百科

这是一个看起来像墨西哥帽的表面,它具有非常好的属性,它具有很好的属性,可以将其近似为两个高斯的差,并且可以检测类似斑点的特征。
DoG (Difference of Gaussian)是灰度图像增强和角点检测的方法,其做法较简单,证明较复杂,具体讲解如下:
Difference of Gaussian(DOG)是高斯函数的差分。我们已经知道通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,即去噪过程,这里的Gaussian和高斯低通滤波器的高斯一样,是一个函数,即为正态分布函数。
那么difference of Gaussian 即高斯函数差分是两幅高斯图像的差,

具体到图像处理来讲,就是将两幅图像在不同参数下的高斯滤波结果相减,得到DoG图。过程:
处理一幅图像在不同参数下的DoG
A = Process(Im, 0.3, 0.4, x);
B = Process(Im, 0.6, 0.7, x);
a = getExtrema(A, B, C, thresh);
其中:
function [ out_img ] = Process( img, sig1, sig2, size )
是求图像DoG的结果,两个高斯平滑参数分别为sig1和sig2,结果如下:


根据DOG求角点
Theory:DOG三维图中的最大值和最小值点是角点

现在,我们在一个一维示例中看到了如何取一个像素
我们将此作为sigma的函数,最大值将给出内在尺度。在这里,我们将其绘制为在不同比例层上的xy,我们将看到实际上有一个sigma,在这里用其长度表示最适合我们的存储结构。
在实际算法中,它的工作方式是这样的,我们有x y图像,并且在比例空间中有几张图像。因此,对于一个点,它在相同规模上具有八个邻居,在较粗规模上具有九个邻居,而在较精细规模上具有九个邻居。在此3x3x3邻域中,如果此点具有拉普拉斯算子的最大响应,则可以说这是SIFT关键点。
我们真的建议您去下载牛津大学教授Andrea Vedaldi的一个非常著名的软件包,它称为VLFeat。


规范化
让我们在一维情况下看一下这个拉普拉斯算子。假设原始图像的斑点较大,如左侧的矩形
让我们用这个带有几个信号的拉普拉斯算子。如果我们开始模糊,模糊,然后再次模糊,则最后信号将淡出,并且没有任何振幅。
这就是为什么我们需要进行标度归一化,以便最后,始终在曲线上的整数将保持不变,并且不会消失。

在某些时候,如果我们在这些图像中采用特定的位置x,我们将看到我们的处置将达到最大值。这就是内在尺度,这就是我们获得本地邻域的尺度并自动匹配的方式。
对这些DOG图像进行归一化,可有很明显的看到差分图像所蕴含的特征,并且有一些特征是在不同模糊程度、不同尺度下都存在的,这些特征正是Sift所要提取的“稳定”特征:

尺度的选择


特别注意:在于多尺度与多分辨率。sift算法中,同一组(octave)中的多层图像分辨率是相同的,只是高斯平滑时使用的参数不同,但这并不影响分辨率。


invariant 恒定性

因为拉普拉斯算子是各向同性的,并且(x,y,σ)的最大值对于旋转是不变的

由于检测到内在尺度(圆的大小),所有圆将被归一化为16x16区域
The descriptor should be also rotation invariant 旋转不变性

•第一步:找到每个色块的主导方向
•第2步:旋转色块以沿x轴指向


因此,我们又有了这个圆,我们对旋转所做的就是获得所有方向的直方图,这些就是对比度方向或渐变方向。最大值定义了局部方向。这在局部定义了一个我们旋转的框架,以便主导方向与x轴对齐。这样,旋转信息消失了,我们收到了旋转不变邻域。
从单元中提取特征描述符

•计算图像梯度
•沿单元积累梯度
•表格图片描述符
现在,我们将带状区域划分为方差旋转,因为我们实际上已对其进行局部旋转并进行了缩放。因为我们已将所有内容归一化为邻域的相同大小。
我们获取所有梯度方向的直方图。

我们不对整个邻域进行直方图绘制。我们所做的是,将其分成小块,然后对这些块进行直方图处理。

对于四个直方图块,这给了我们类似的东西。
正如我们看到的真实图片一样,每个点都与这4 x 4网格相关联。
图片中的块本身就是直方图。

图中每个框框含有8个方向,周围有8个框框。
It is a histogram on 8 orientations with 8 bins.
So we have 8 bins in 8 block of this grate.
And having 16 grates, we have at the end 128 values for all the bins of orientations.
您可以在图片中看到它用很小的绿色箭头表示。
您会看到直方图,该直方图在此4 x 4网格的每个块上局部占主导。
例如,您看到当我们在棋盘的一角时,我们有两个正交的主导方向。这个128 x 1的向量不包含有关其原始缩放比例和原始措辞在图像中定向方式的任何形式。该信息仅与点x一起出现,y是sigma和beta值。
SIFT检测示例

描述符是一个128x1向量,它与σ,θ一起表征关键点。

我们看到了几个SIFT功能和相关的描述符。
一些SIFT图片具有很大的固有比例。
他们代表着大圈子。
其中一些旋转角度倾斜30度。
Create Image Mosaic
- Get an image pair
- Establish correspondences between matching features
- Keep only consistent matches (inliers)
- Compute homography and warp 2nd image
- Repeat to extend the mosaic


•SIFT检测器可以自动
–选择比例
–计算主导轮换
•SIFT描述符
–是梯度方向直方图的网格
–在关于比例和旋转标准化的区域上
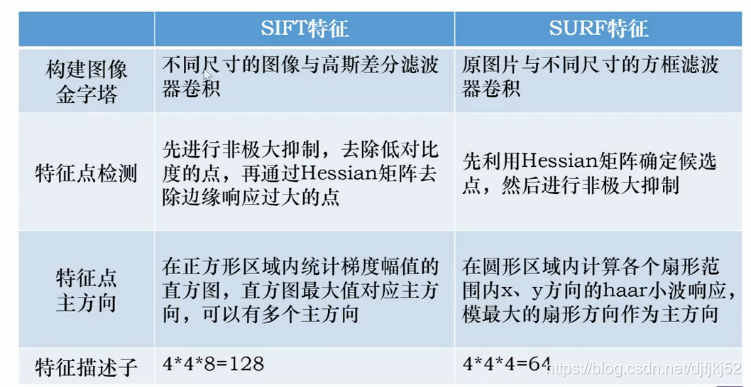
附件:SURF与SIFT

SVD

Singular Value Decomposition。分解得到的U矩阵是一个列正交矩阵,取其任意一列(n×1)将它的转置(1×n)与其相乘,得到的结果为1。也就是说U的每一列的模长为1。取U的第i列(n×1)与第j列的转置(1×n)相乘结果为0,也就是说U的每一列都互相垂直。VT有和U类似的性质,每一行都互相垂直,每一行模长为1。UT和U相乘、VT和V相乘结果都是单位阵。而对于D,对角线元素即为奇异值,且依次递减,最小为0。
奇异值其实反映了U的某列对于A的贡献(这也就是为什么最小为0的原因),如果奇异值非常大,则表示贡献非常大,如果接近于0,则表示U的这一列几乎没有什么贡献,去掉也没什么关系。这就是主成分分析了。可以注意到,如果A是m×n,那么U和A大小相同为m×n,D和VT都是n×n。
这里需要注意的是SVD分解并不是只有上面说的这一种形式。上面这种形式是行>列的情况下,使奇异矩阵为方阵时的分解结果。
Comparison and Conclusion
http://zhaoxuhui.top/blog/2019/11/09/svd.html#5comparison-and-conclusion
对于一个m×n的A矩阵,在不同库下的SVD分解结果如下所示。diag表示将奇异值向量转成奇异矩阵(对角阵),trans表示转置。

由上图可以看出:
Eigen与OpenCV一样,保持奇异矩阵为方阵,大小与原始矩阵的最小维度相同。不同的是Eigen返回的是V,而OpenCV返回的是VT。所以在恢复矩阵时,一个要先转置再乘,一个直接乘。
Matlab与Numpy相同,通过保持奇异矩阵与原始矩阵大小相同,使得U、V都为方阵且不随原始矩阵大小关系的变化而变化。不同的是Matlab返回的是奇异值矩阵、V,而Numpy返回的是奇异值向量、VT。所以在恢复矩阵时,一个要先转置再乘,一个构造奇异矩阵后直接乘。
其实从上面也可以看出,SVD分解有两类不同形式。一类是使中间的奇异矩阵与原始矩阵大小相同(如Matlab和Numpy采用的方法),这样的好处是U、V分别为方阵,大小分别为原始矩阵的高和宽,且不会随原始矩阵行列关系变化而变化;另一类是保持奇异矩阵为方阵(如Eigen和OpenCV采用的方法),U、V随原始矩阵行列关系变化而变化,又可以细分为行>列和行<列两种情况(行列相等的情况两种都适用)。
因此,对于一个形状为m×n的A矩阵,对其进行SVD分解,可以有以下情况:
当奇异矩阵与原矩阵相同大小时:
当奇异矩阵为方阵且原始矩阵行>列时:
当奇异矩阵为方阵且原始矩阵行<列时:
形象理解SVD=Basis+transformed Address

理解SVD的思路可以把SVD当作是Basis+transformed Address。如果把A当作是一个曲线,U可以理解为一些表达曲线的基本形状,VT表示了这些形状所在的不同位置,D则表示了这些形状的缩放大小。最后通过它们就可以恢复出原始曲线的样子。如下是利用SVD恢复某张图像的效果。

可以看出,只需要取U的前20列(主元素分析)。
SVD可以得到Rank

借助SVD分解,我们也可以得到矩阵A的秩(Rank),即等于奇异值矩阵 中非零对角线元素的个数。根据这个性质可以得到SVD分解的另一个用途是,利用SVD分解可以获得指定秩的矩阵。先将矩阵A进行分解,然后取奇异矩阵中前m个非零元素,重新组成矩阵,这个重新组成的矩阵的秩即为m。
SVD求逆
SVD分解的另一个用途是对矩阵求逆

A-1=VD-1UT。
齐次与线性
https://www.zhihu.com/question/19816504
- 齐次坐标
下面我要解释的齐次坐标(homogeneous coordinates)是我所熟悉的计算机视觉和图形学这两个领域中经常要用到的概念,同时,坐标也是一般人都可以理解的东西。
二维空间中的一个点是用二元组(x,y)表示的。我们可以增加一个额外的坐标得到三元组(x,y,1),同时我们声明这是同一个点。这看起来完全无害,因为我们可以很简单地通过增加或者删除最后一个坐标值来在两种表示方式之间来回切换。
现在,有一个很重要的问题是:最后一个坐标为什么需要是1?
在这里,我们要再给出一个定义,即当k非零时,所有形如(kx,ky,k)的三元组都表示同一个点,比如(x,y,1)和(2x,2y,2)就表示同一个点。由此我们就可以引出齐次坐标的定义,即给定一个二维点(x,y),那么形如(kx,ky,k)的所有三元组就都是等价的,它们就是这个点的齐次坐标。对每一个齐次坐标,我们只要把它除以三元组中的第三个数,即可得到原始的二维点坐标(这就是@祝文祥的答案中所说的同比收缩的一个例子)。
不过我觉得,从字面上来看,齐次坐标这个叫法还是不那么形象,不过看看和齐次对应的英文单词homogeneous,我们会发现这个词有时还会被翻译成“同质”,表示某一类东西拥有一些相同的性质,这么来看的话,还是挺形象的吧。
需要再次注意的是这里的k是非零的,那么如果k=0会怎样?因为除数不能为0的缘故,所以似乎没有任何二维点是和(x,y,0)对应的。事实上,(x,y,0)就是无穷远处的点。以前,我们用(x,y)是无法描述二维平面上的无穷远点,但当我们引入齐次坐标之后,就可以用(x,y,0)来表示无穷远点了。这就是引入齐次坐标的一个好处。
以上关于齐次坐标的内容翻译并修改自《Multiview Geometry in Computer Vision (2nd Edition)》第2页第9行开始的两段。
- 线性
再来说说“线性”。和“齐次”类似,带“线性”的概念也很多,下面我也会给出一个具体的线性的东西来解释,以防过于抽象。
“线性变换”(Linear Transformation)同样是计算机视觉和图形学中经常用到的东西。通常,我们会用一个矩阵来表示一个线性变换,对于二维空间中的线性变换,我们经常用3x3的矩阵来表示。当给定一个线性变换矩阵之后,我们把它和一个齐次坐标一乘就可以得到经过变换后的齐次坐标了。
那么为什么我们要管这种变换叫线性变换而不是弯性变换呢?这里抛开线性的数学定义不说,线性变换有一个重要的性质,非常形象地表达了这一概念,即保共线性。具体地说就是,在线性变换之前处于同一条直线上的3个点,经过线性变换之后必定还处于同一条直线上。换句话说,如果你画了一条直线,这条直线在经过线性变换之后它必定还是一条直线。
所以说,线性变换最喜欢直线了,除了直线以外的东西,比如角,在经过线性变换之后可能就完全不一样了,此外,还有长度、面积、平行等等,线性变换都不喜欢,不保证它们在变换之后还能维持原样。
- 齐次方程
齐次和非齐次更倾向于其代数意义。很容易从字面上理解处“齐次”的含义就是次数相等,例如

都是齐次多项整式。整式的次数定义是——次数最大的项的次数,项的次数(单项整式的次数)的定义是——所有变量的指数之和。

