线性与非线性
线性与非线性更倾向于其几何意义。从字面上看“线性”就是“具有线的特性”，这里的“线”指的是直线。我们知道，在平面上，直线对应的都是一次方程，因此“线性”在代数意义上就是“一次”，也就是说“一次”就是“线性”，“线性”就是“一次”，也就是关于某几个“量”（标量，矢量，函数，矩阵，导数）的表达式中这些“量”的次数最高只能是一次，且没有这些“量”的乘法、除法、指数和对数运算。表达式中可以包含常数项，因为常数项的次数为0，不超过1。
“非线性”就是“量”的次数不等于1，或者“量”参与了其它运算的情形，比如指数函数就不是关于自变量的线性函数。
齐次与非齐次
齐次和非齐次更倾向于其代数意义。很容易从字面上理解处“齐次”的含义就是次数相等，例如
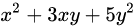
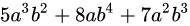
都是齐次多项整式。整式的次数定义是——次数最大的项的次数，项的次数（单项整式的次数）的定义是——所有变量的指数之和。
非齐次就是各项次数不一致的意思。
齐次方程
对于方程而言， “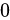
”是任意次的，因为0乘任何数（不包括无穷大）都为零，因此0乘任何单项整式也都为零。齐次方程的含义是——等式两边各项次数都相等的方程，如果将带有变量的项放到等式的一边，则另一边只有0。0是任意次项，因此只要等式另一边齐次，方程就是齐次的。（当然也可以这样理解，无论怎样移项，等式两边各项次数都是相等的，所以这样的方程就是齐次方程）
齐次线性
齐次线性——那就更简单了，每项都只能含有一个变量且其指数只能为1，不能含有常数项（否则出现0次项，就不齐次了）。
P. S.：微分方程中有两种齐次方程，实际上可以这样称呼以便区分，一类是变量齐次微分方程，一类是导数齐次微分方程。能将一阶微分方程化为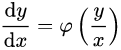 
的方程就是变量齐次微分方程，至少书上所有这样的微分方程，如果看微分前面的表达式，计算里面的次数都可以发现它们的次数是相等的。而 
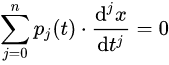就是导数齐次微分方程，很明显这个微分方程关于各阶导数和原函数的次数都为1，而右边是0，0是任意次的，也就可以被认定是一次项。
齐次坐标
任何一个n维坐标它表示的一个点，在n+1维空间中的那n+1维是丢失了一维，所以在n维中每一维次数都是1，而第n+1维可以认为次数为0 ，如(x,y,1)，它前两维次数都是1，而第三维次数是0-因为任何数的0次方始终为1，这样就不是齐次的，而如果第n+1维的次数也为1，比如(x,y,z)，该坐标就变为齐次坐标，而我们把这个坐标每一维都除以z就得到(x,y,1)，又变成非齐次坐标，但它能反映一个二维坐标（x,y）这是一个二维齐次坐标。几何理解，齐次坐标是相对于低一维度的空间来说的，可以表示该坐标到该空间原点的连线上的所有点。