你站在桥上看风景,
看风景人在楼上看你。
明月装饰了你的窗子,
你装饰了别人的梦。 —《断章》卞之琳
用现代诗人卞之琳先生的诗《断章》来引入今天的主题,再合适不过了。诗中描述的相对性正好可以形象的理解三维重建坐标系的相对关系。看风景的你构成以自我为中心的坐标系,目光所至是你的坐标系方向;楼上人构成以他为中心的坐标系,目光所至构成他的方向,两坐标系之间蕴含着几何转换关系。
图示:(本人灵魂画作,诗的意境完全被破坏了哈哈!)

Structure Form Motion
做三维重建,要是没听说过Structure Form Motion(SFM),那你一定属于两类:
-
刚入门的小白
-
做了好几年的纯摄影测量方向老人
哈哈,开个玩笑,我就是做了好几年的摄影测量老人,其实是叫法不一样而已,摄影测量学课本中没有SFM这样的词,而是叫相对定向+前/后方交会+光束法平差,SFM是计算机视觉领域的叫法,其实理论完全一样。当然现在计算机视觉和摄影测量融合的很深了,而计算机视觉的受众群体也要庞大很多,所以本篇其实是纯计算机视觉角度的讲解。
Structure Form Motion,顾名思义,从运动中恢复结构。
这里的运动指相机的运动,可以人拿着相机一边走一边拍照(或者一边转圈一边拍),还可以汽车载着相机一边兜风一边拍照,还可以飞机拖着相机一边飞翔一边拍照,还有卫星…,不说了,真羡慕相机!反正一句话,让相机运动起来。
而结构是指三维结构,包括两类:
-
相机位姿
-
场景三维数据
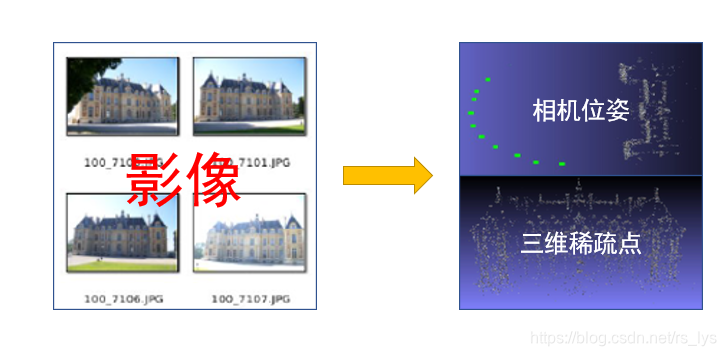
我们来看张图(图片来自著名的开源项目OpenMVG):

图像的上半部分是输入的图像(通过移动相机拍摄的各位置的图像),下半部分是通过SFM恢复的相机位姿和场景三维数据。我再重新组织下图,你们看看:
我为什么把SFM放开始来说呢,这和坐标系和关键矩阵有啥联系?
坐标系和关键矩阵正是SFM的几何基础,如果你不做SFM,只做立体匹配或网格构建什么的,那你即使不知道坐标系和关键矩阵,你也能做出不错的成果,但是如果你做SFM不懂它俩的话,那你可就要面壁思过了。
我再啰嗦一会再入正题!SFM怎么做?
- 1 图像特征提取与匹配
- 2 相机位姿解算
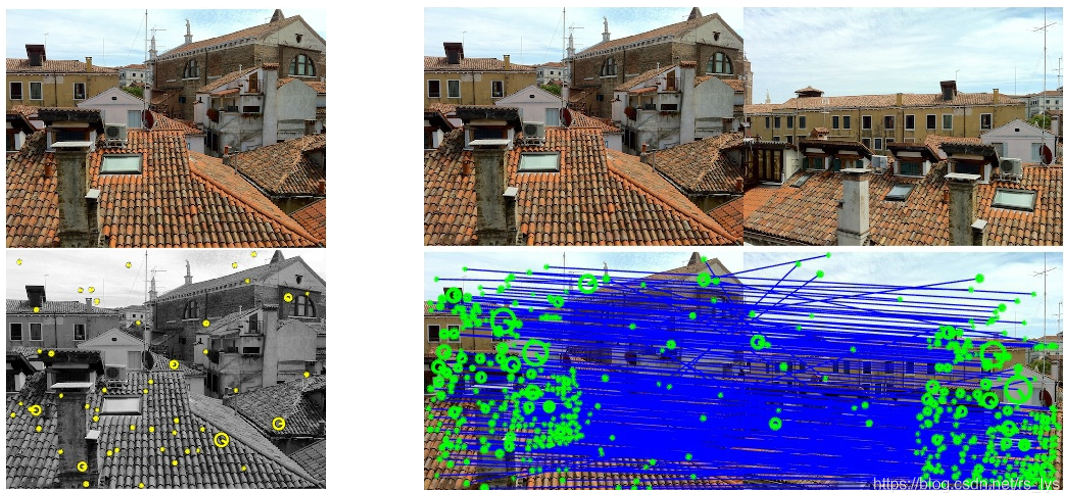
图像特征提取与匹配是纯二维视觉,我们就不细说了。
相机位姿解算就和今天的主题100%紧密相关。我打个比喻,增量式SFM就是把一堆图像先点个鸳鸯谱,分成一对对,再对最恩爱的一对鸳鸯做图像特征提取与匹配,然后通过特征匹配结果求解关键矩阵,并分解关键矩阵得到鸳鸯间的相对位姿。之后不断的加入新的鸳或鸯,直到所有鸳鸯形成一个紧密相连的鸳鸯群。(我突然感觉这个比喻似乎不太合适,有被和谐的风险,不要举报我!)
言归正传,图像/位姿/关键矩阵,这是我提炼的三个关键信息。图像到三维位姿,就需要坐标系转换(二维到三维当然要坐标系转换了);而关键矩阵,是计算相机位姿的关键。
我就直接告诉你们有三个关键矩阵F、E、H:
- F:Fundamental matrix,基础矩阵
- E:Essential matrix,本质矩阵
- H:Homography matrix,单应矩阵
至于有多关键,我们先聊聊坐标系,再聊关键矩阵。
坐标系
有坐标系,才有位置概念,这是基础。
二维的图像到三维的结构,那必定有个坐标系的变换。还记得文章开头的灵魂画作不(想你们也不会忘),里面有两个坐标系,主人公坐标系和看风景人坐标系,他两所看到的景物大小尺度是一样的,只不过俩站的位置、眼睛朝向不一样,存在一个旋转平移变换。在三维重建中,我们分别对应着相机坐标系和世界坐标系,相机坐标系以相机为中心,朝着景物的方向,世界坐标系根据应用可随意设置,比如大地测量,就是大地坐标系。
景物在相机传感器上成像,形成一张二维图像,图像像素所在的坐标系就是影像坐标系。这三个坐标系就是我们今天要了解的视觉三维重建坐标系统:
- 影像坐标系
- 相机坐标系
- 世界坐标系
影像坐标系
影像坐标系是以二维影像为基本建立的坐标系,描述像素点在影像上的位置,分为以像素为单位的uv坐标系以及以物理尺寸为单位的 坐标系。 坐标系以图像左上角为原点, 轴和 轴分别平行于图像平面的两条垂直边( 轴朝右, 轴朝下); 坐标系以相机主光轴与像平面的交点(主点)为原点, 轴和 轴分别与 轴和 轴平行且方向一致。如图所示:
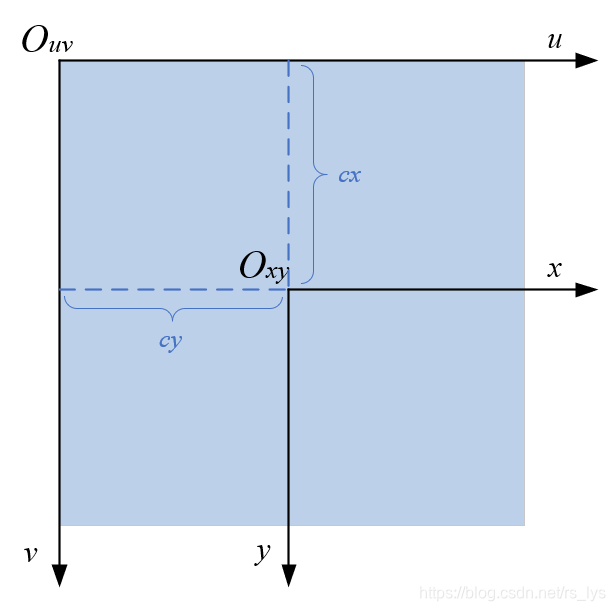
我们往往要把物理坐标系转成像素坐标系,它们坐标系平行,原点的偏移量为主点坐标( ),像素大小的物理尺寸为( ),则转换公式为:

相机坐标系
相机坐标系从相机的视角来描述物体在三维空间中的坐标。以相机中心为原点, 轴与 轴分别与影像坐标系的 轴与 轴平行,且方向一致,根据右手坐标系规则得到 方向。相机坐标系是物理尺寸单位,如图所示:

相机中心到图像平面的距离为焦距 。
相机坐标系转换为影像坐标系是坐标系从物理空间到像素的关键一步,由于坐标系平行,所以物体在影像坐标系和相机坐标系中的位置存在一个等比例关系(下图左),根据等比关系可知相机坐标系坐标( )到影像坐标系坐标( )的转换公式如下图中所示,下图右为其矩阵形式。

|

|

|
但是我们操作像素一般都是直接用图像的 坐标系,好办啊,再把 坐标转成 坐标就行了,如图:

把
拿到等式左边来变成下图左的形式。
我们再来个简写,假设一个点在图像上坐标为
,在相机坐标系的坐标为
,则下图左可简写为下图中的形式,式中
就等于
,是点在Z方向上离相机的距离,这个简写方式后面会用到。
而 就是大名鼎鼎的相机内参矩阵。

|

|

|
世界坐标系
世界坐标系是从意义上和相机影像无关的坐标系,它只和你的应用需求有关,往往是完全固定的,无论你相机如何移动,我自岿然不动!
比如我们做室外导航地图,那世界坐标系肯定是大地坐标系,即以参考椭球面为基准面建立起来的坐标系;而如果我们做小物体的三维重建,只关心物体尺寸,不在乎绝对位置,则可以建立一个位置朝向都比较随意的坐标系,比如在标定板上,比如在相机本身。
那有人就有疑问了,你建立的这么随意,那他意义在哪呢?
世界坐标系最大的意义就是他是恒定的,恒定意味着统一,你可以把多个位置重建的三维数据都统一到一个世界坐标系下,它们就有了和真实世界一样的相对位置关系,这样你才能从三维数据中了解A的左边是B,B的左边是C。这点相机坐标系是没法做到的,因为相机坐标系以相机为中心,而相机又在不断地移动,所以在相机坐标系中,你在位置1拍摄的场景和你在位置2拍摄的场景就会重合,但是真实世界中两个位置明显不同。
那世界坐标系和相机坐标系怎么转换?
世界坐标系和相机坐标系都是以物理尺寸为单位,所以他们尺度一致,但是原点不一样,朝向也不一样,所以他们存在一个刚性的旋转平移。
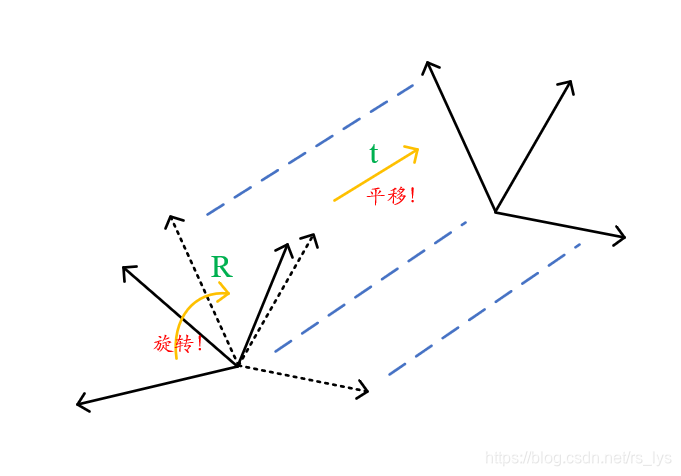
旋转矩阵 ,平移矩阵 ,是大名鼎鼎的相机外参矩阵。
世界坐标系到相机坐标系的转换公式如下图左。
另一种表达方式是设相机中心在世界坐标系中的坐标为 ,则公式变成下图中。(这种表达方式外参矩阵就是R和C)
两式等价, 。我们又简化一下,得到下图右,其中 为世界坐标。

|
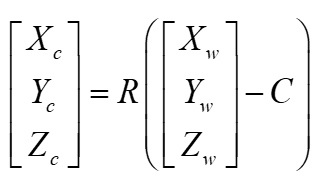
|

|
既然世界坐标系可以转到相机坐标系,相机坐标系又可以转到影像坐标系,那世界坐标系就一定能直接转到影像坐标系咯?真聪明,请看如下推导:
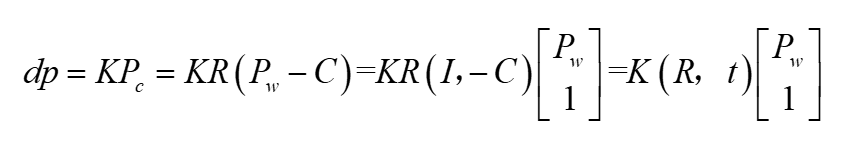
从上面读下来,我相信这个你绝对能看懂了。
咱们引入投影矩阵 , 或 ,上式变为:
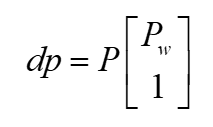
这就是世界坐标到影像坐标的转换关系,有了世界坐标系,就可以直接计算影像坐标。什么,不知道 ?别忘了 是齐次坐标哦,意味着不需要知道 ,把 一起算出来,再把第3个分量归一化为1就得到像素坐标(就是第1、2分量都除以第3分量)。
反过来,通过影像坐标,就没法直接计算世界坐标了,就需要知道 ,也就是深度信息。要是能直接计算那可不逆天了,视觉三维重建工程师得全下岗了!
坐标系咱们就说到这里。大家会推导投影矩阵就算是通关了。
下面来看看关键矩阵。
关键矩阵(基础矩阵F、本质矩阵E、单应矩阵H)
先阐明:关键矩阵描述的是两张影像的像素点之间的对应关系,用来做SFM两张图像间的相对位姿变换。
基础矩阵和本质矩阵
先不直接告诉你们这三个关键矩阵是什么含义,我们一步步推导开来,看到最后你们会恍然大悟,哦,原来是这样!
我们先来看两张影像构成的双视模型。

留意图中各个符号所表达的含义。首先假设世界坐标系和左视图的相机坐标系重合。则右视图相对于左视图的旋转 和平移 ,等同于其相对于世界坐标系的外参矩阵 。
相机的内参矩阵 多了个 ,他是图像的切变参数,一般是0。
我们只讨论单相机的情况,就是同一个相机在两个位置拍摄了两张影像。开始推导:
设空间点P在世界坐标系中的坐标为 ,因为世界坐标系和左视图的相机坐标系重合,所以在左相机坐标系坐标也为 ,而在右视图相机坐标系中的坐标为 。基于相机坐标系到影像坐标系的转换公式,得到如下转换式(不熟悉这个公式的请回到前面关于相机坐标系到影像坐标系转换的段落再复习一遍):

左边的 是齐次坐标,如果对空间点也取齐次,即将空间点归一化到 的平面, 就变成了1,上式变成

该等式在齐次意义上成立,也就是乘以任意非零常数依旧相等。
咱们把 拿到等式左边来,则公式变成:

设

可得

两边同时叉乘 ,可得

自己叉自己等于0,再两边同时点乘 ,得

叉乘可以等价于用反对称矩阵来点乘, 的反对称矩阵表示为 ^,上式变成

这个式子简洁吧,如果我们再把 换算成 ,则变成另一种形式:

这两个公式是完全等价的,它们就是计算机视觉里常听到的对极约束,几何意义是 共面(见下图)。我们把上面两式像点中间夹着的部分记做两个矩阵:本质矩阵E:Essential matrix和基础矩阵F:Fundamental matrix。得到更简洁的表示形式:

|

|

|
本质矩阵和基础矩阵的区别是:本质矩阵是和 建立的关系,而 是由内参矩阵 和像素坐标 计算出来的,所以本质矩阵使用的前提是内参矩阵 已知;而基础矩阵直接和像素坐标 建立联系,所以不需要已知内参矩阵。
还记得我们的SFM吗,特征匹配就是要得到式中的 或 ,然后通过上面等式求解 或者 ,再通过 和 分解得到 和 。至于求解方式,比如8点法、5点法、奇异值分解之类的,本篇就不细说了。
等等,还有一个单应矩阵呢!
单应矩阵
单应矩阵描述的两个平面之间的变换关系,若场景中的点都落在一个平面上(比如机器人看着一块白墙或望向天花板),则可以通过单应矩阵来进行相对位姿估计。如图所示:
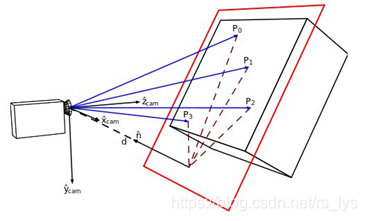
已知 所在的平面方程可表示为

式中, 为平面法线, 为摄影中心到平面的距离,推导:

这就是两个像素的单应性关系,把 前面的部分记为单应矩阵H:Homography matrix。

同样的套路,通过特征匹配获得的 ,计算 ,再分解得到 。
好了,本篇就到这里吧,讲多了大家也难全记住,希望能够对大家有所帮助。本篇公式推导多,但不复杂,需要耐点心。
感谢观看,敬礼!