写在前面

本文出发点是对Hyperbolic Nerual Network做一个简短的调研,旨在对这个领域做一个不甚完整的描述.

考虑到没学过相关方面的数学知识,paper也只是挑了比较著名的,因此本文更偏向于直觉上的描述,比较适合想要对此领域先有一个直观感觉,然后深入研究的需求.

先推荐一下合适的非paper材料:

先从欧式空间说起

目前几乎所有模型都是基于欧式空间.比如经典的Word2Vec,我们利用向量在空间中合适的分布来表征语义信息.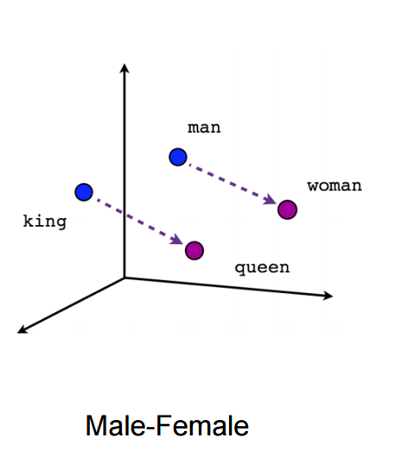 w2v

我们通常使用向量距离来表示这种语义信息,如相似的实体距离较近,无关的实体距离较远;特别的向量距离具有语义上的信息,正如经典的women-men=queen-king;也比如trans系列.我们认为距离也是这种语义信息的表达形式之一.

那么我们为什么要使用欧式空间呢.因为它最符合直觉,简单直观.这是一个被深入研究且广泛使用的空间,我们可以很自然的在这个空间中继承推广一些向量操作,如向量加减法,向量内积,矩阵乘法,定义体积面积等.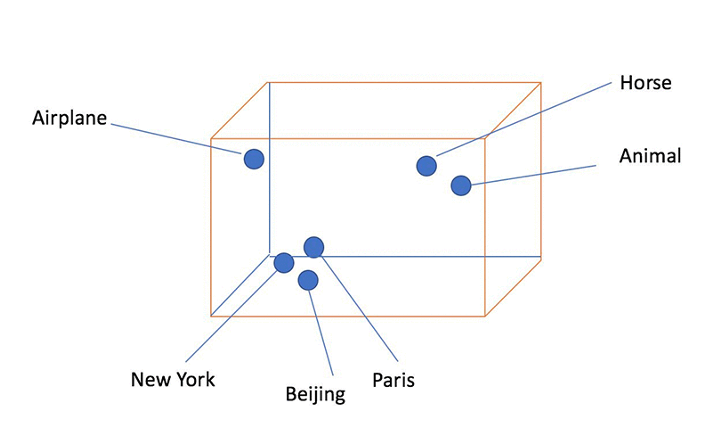 euler

然而欧式空间在简单直观的代价下也有一些限制.

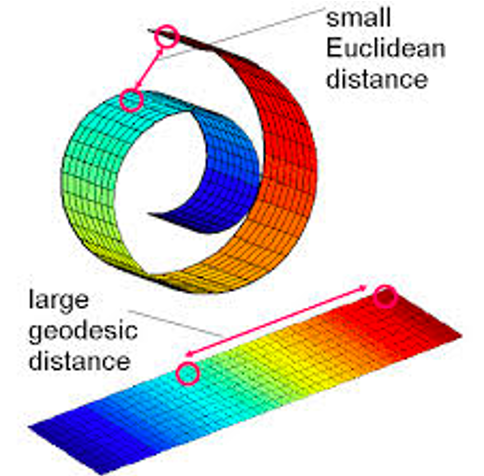
它只能学习到平坦的流形,如swiss roll,不做展开,欧式空间的距离就会与真实距离产生极大地偏差.
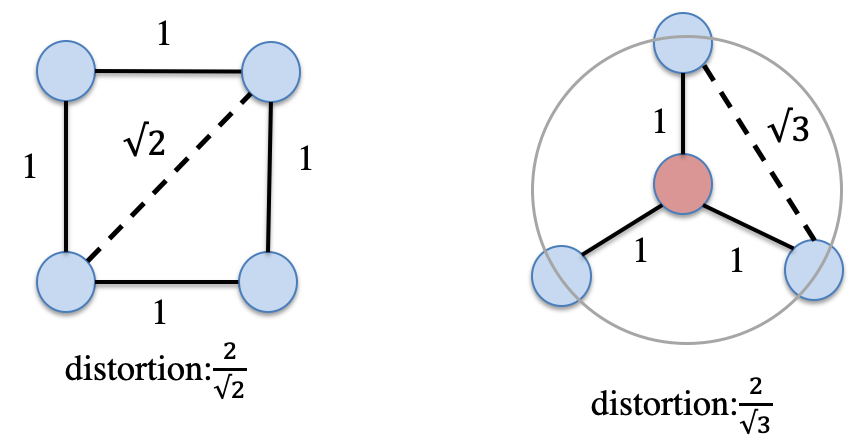
欧式空间不能无失真的将图嵌入到空间中,它对图是有损嵌入.考虑如下左图的例子,针对图距离而言,左下角与右上角距离为2,然而嵌入到欧式空间中,它的距离会畸变为sqrt(2),可以很直观的想象在R2中是不可能无损的嵌入这个正方形的,因此它会坍缩为直线,而这种情况左上角与右下角距离也不满足2的约束.右图也同样如此.
欧式空间是不足以容纳树形数据的.一个很显然的结论是层次结构的数据随着层数的增加,其节点数是指数级膨胀的.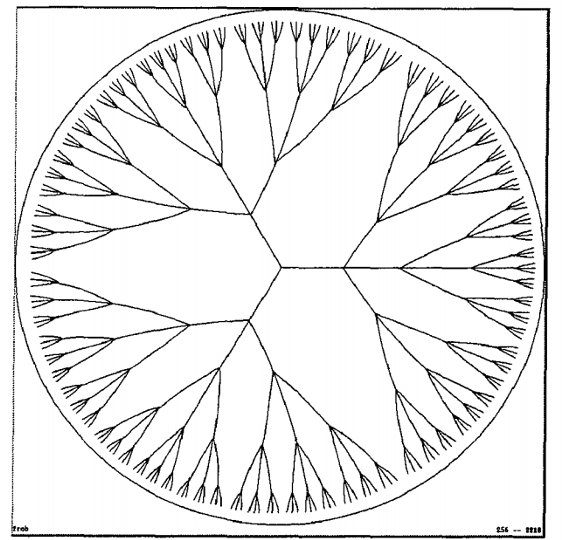而欧式空间,无论维度多高,其空间大小始终是多项式量级.如果我们想要对树形节点学习到好的表示,不妨考虑用至原点的距离来代表节点处于第几层,可以预见到随着层数增长,这层空间会充斥着向量,可能第一层我们只需要将空间一分为三就能学习到好的向量表示,到了第r层,我们就需要将空间划分为非常小的块才能学到好的表示.而这对模型学习是非常不利的.

双曲空间天然适合层次数据

首先,双曲空间是不能在实际生活中被表现出来的,我们只能通过数学形式或者想象来表现它,至于如何想象可以参考youtube上的一些模拟实验.

然而我们可以先给出一些直接的结论来论证我们的一些观点,然后再通过实际的双曲模型来进行直观的理解.

Hyperbolic Space(双曲空间)能够与欧式空间构建共形映射，使得向量夹角不变。因此如果不考虑向量长度,双曲空间表达能力不会弱于欧式空间.如果我们在上游任务构建了合适的双曲embedding,下游任务只使用它的夹角相似度,这一特性就会展现出用处.
任意带权树能够以任意小的失真被二维双曲空间嵌入[1],这一点即使是在无限维的欧式空间也不能被保证[2]。因此双曲空间对树形结构表达能力更强.
双曲空间被视为连续版本的树，其周长与面积增长速度为指数量级。可知双曲空间更开阔，能够容纳树形数据指数级的增长,从而保证叶子节点也能更好地被均匀分开.

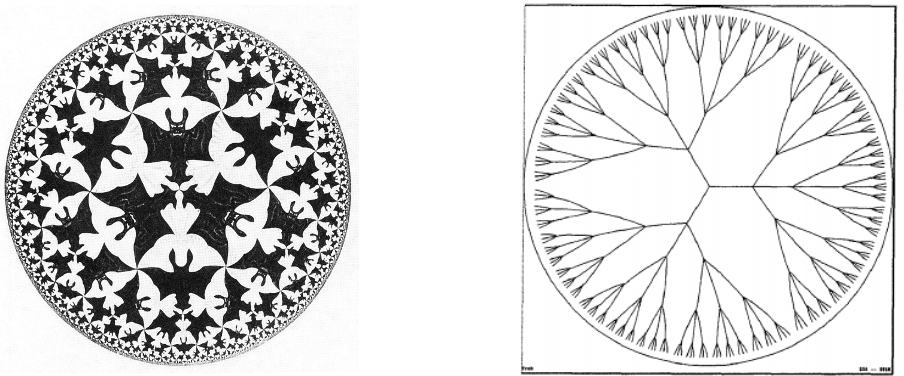
双曲空间的一些实际例子

Poincaré Ball[3]

Poincaré Ball是一种典型双曲空间模型.

可以认为他的定义域为半径为1的圆盘.
\(\mathcal{B}^{d}=\left\{\boldsymbol{x} \in \mathbb{R}^{d} \mid\|\boldsymbol{x}\|<1\right\}\).相对应的在这个空间上向量之间的距离是如下定义.\(d(\boldsymbol{u}, \boldsymbol{v})=\operatorname{arcosh}\left(1+2 \frac{\|\boldsymbol{u}-\boldsymbol{v}\|^{2}}{\left(1-\|\boldsymbol{u}\|^{2}\right)\left(1-\|\boldsymbol{v}\|^{2}\right)}\right)\).

距离函数可以直观的通过下图理解: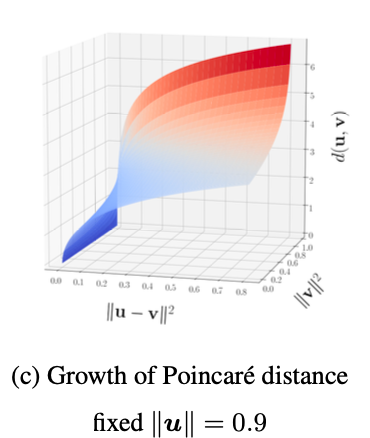 care_dis 可知当向量越接近边界,其距离会呈现指数级的增长,而当向量越接近圆心,其距离会越短.

如果我们将树投影到这个空间,我们利用节点至原点的距离来正比于树中的层级关系,则会呈现如下形式: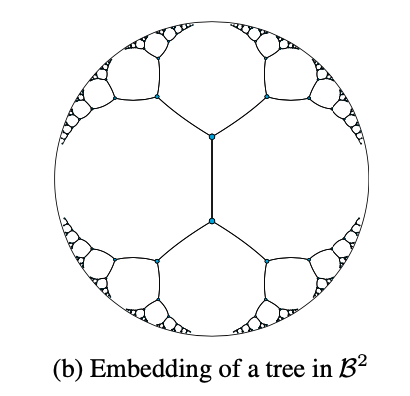 tree_care .图中每条线段长度实际上是相等的,虽然在欧式空间中看上来越接近边界其长度越短.这种特性可以认为是在有限的空间中实现了无限的距离定义,其边界指数增长的特性也能保证了足够的空间来容纳树形结构.

因此我们可以有这样一种直觉,树中第r层的节点因为数量的原因,在学习过程中,模型会根据数量多少将其推到合适大小的空间位置中,从而更好的均匀分开.对于前几层的节点,空间足够,因此不会特别推离原点,对于后几层的节点,数量指数级增长,就需要更远的距离,更宽阔的空间来均匀分开,因此会将其推向边界.而这一点,因为欧式空间是均匀分布(或者说跟不上增长速度),就不存在所谓的将数据推开的趋势.我们通过下图实验结果的可视化来验证我们的直觉,其中上面是Poincaré Embedding,下面是欧式Embedding.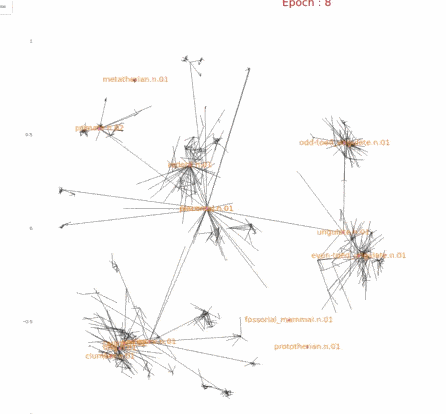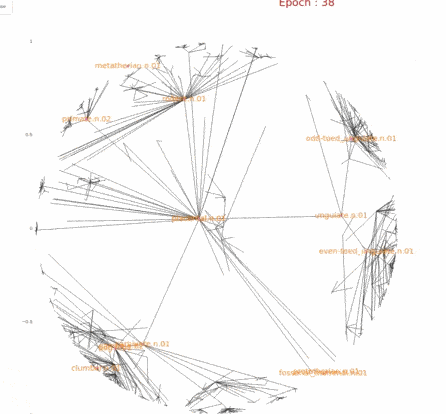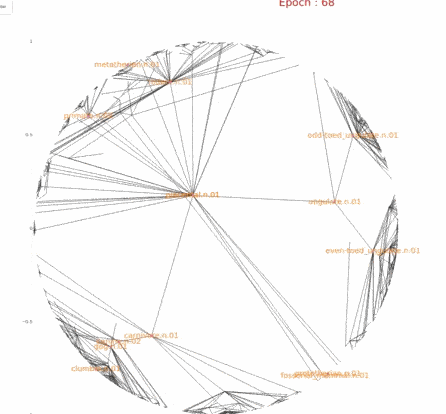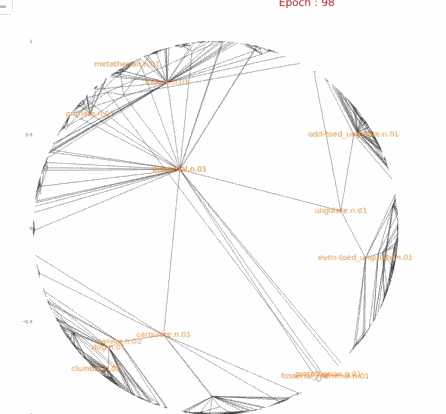

因此我们可以认为双曲空间的这种特性(主要指距离定义)为数据层次结构提供了一种几何先验.

Lorentz model[4]

Lorentz model也是典型双曲空间模型。我们无须知道其具体的特性,只需了解它避免了Poincaré Distance的数值不稳定性,因为后者涉及到趋近于0的除法。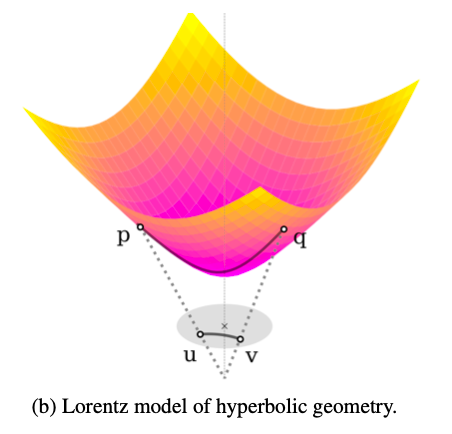 lorentz

该模型定义域为\(\mathcal{H}^{n}=\left\{\boldsymbol{x} \in \mathbb{R}^{n+1}:\langle\boldsymbol{x}, \boldsymbol{x}\rangle_{\mathcal{L}}=-1, x_{0}>0\right\}\),其距离函数定义为\(d_{\ell}(\boldsymbol{x}, \boldsymbol{y})=\operatorname{arcosh}\left(-\langle\boldsymbol{x}, \boldsymbol{y}\rangle_{\mathcal{L}}\right)\).可知就数学表达式上来说该模型数值稳定性比Poincaré Ball还是要强很多的.

为什么我们要考虑这个模型呢,因为有一个好消息是它能和Poincaré Ball构成双射.因此我们可以在Lorentz model中进行数值优化,然后在Poincaré Ball中进行可视化.具体的我们有:

L->P:\(p\left(x_{0}, x_{1}, \ldots, x_{n}\right)=\frac{\left(x_{1}, \ldots, x_{n}\right)}{x_{0}+1}\)

P->L:\(p^{-1}\left(x_{1}, \ldots, x_{n}\right)=\frac{\left(1+\|x\|^{2}, 2 x_{1}, \ldots, 2 x_{n}\right)}{1-\|x\|^{2}}\)

双曲GNN

遇到的问题

我们讨论了双曲空间的一些实际空间模型,自然地我们要考虑怎么像利用欧式空间一样的利用他们呢.

这里考虑GNN作为代表,但是显然这可以使用到任何NN中.

GNN归根到底是将node features联合图结构信息映射到d维空间中.\(f:\left(\mathcal{V}, \mathcal{E},\left(\mathbf{x}_{i}^{0, E}\right)_{i \in \mathcal{V}}\right) \rightarrow Z \in \mathbb{R}^{|\mathcal{V}| \times d^{\prime}}\)

以GCN作为例子,我们通常要经过feature transform(\(\mathbf{h}_{i}^{\ell, E}=W^{\ell} \mathbf{x}_{i}^{\ell-1, E}+\mathbf{b}^{\ell}\))和aggregation(\(\mathbf{x}_{i}^{\ell, E}=\sigma\left(\mathbf{h}_{i}^{\ell, E}+\sum_{j \in \mathcal{N}(i)} w_{i j} \mathbf{h}_{j}^{\ell, E}\right)\))两个过程.

因此具体的,如果我们要在双曲空间中执行GNN,我们需要考虑如下问题:

Input: Euclidean -> Hyperbolic.我们的输入feature通常是欧式空间下的,因此我们不能直接使用它们.
Feature transform in Hyperbolic.指双曲空间下的非线性变换.
Aggregation in Hyperbolic.指双曲空间下如何对信息做Aggregation.
Activation in Hyperbolic.指双曲空间下的非线性变换.
Output:Hyperbolic -> Euclidean (?).我们的输出显然是双曲空间下的,我们是否能直接使用它呢,这其实是存疑的.正如上文所说,如果我们仅仅使用了夹角相似度信息,其实我们可以直接得到结果.如果我们只需求确定结果,如分类,我们可以直接在双曲空间下做softmax即可.如果我们需要向量的整体分布,假设下游任务使用的也是双曲空间那自然皆大欢喜,假设下游任务使用的是欧式空间,那就必须要考虑将双曲空间下的向量分布转化为欧式空间的分布,不作考虑直接使用显然会破坏其结构信息,模型将毫无意义.
Optimization in Hyperbolic.我们现有的优化方法都是欧式空间下的,要优化双曲空间下的模型,我们需要做进一步打算.
解决了这些问题,我们才能真正构建出双曲空间下的GNN模型.

一些数学上直觉

首先我们必须要明确为什么我们不能直接将一些向量操作直接推广到双曲空间中.不妨考虑Poincaré Ball模型,向量都在单位圆内,如果直接做向量加法,显然向量会超出这个圆范围,因此直接推广其操作是不合理的,我们需要从数学流形上来对其进行严格推广.

TODO

Hyperbolic Nerual Network