【信号与系统学习笔记】—— 连续时间非周期信号傅里叶变换到底有哪些性质呢？【上篇】（important！）

1. 线性

这个和周期信号的傅里叶级数是类似的，我们下面给出定义：
若 $x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω); \quad y(t)\space \underleftrightarrow{\mathscr{F}} \space Y(jω)$
那么我们有： $ax(t) + by(t) \space \underleftrightarrow{\mathscr{F}} \space aX(jω)+bY(jω)$

2. 时移 —— 时域延迟等价于频谱旋转

若 $x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω)$，那么 $x(t-t_0) \space \underleftrightarrow{\mathscr{F}} \space X(jω)e^{-jωt_0}$
这个式子带给我们的启发是：时域是延迟等价于频谱的旋转。 因为频谱 $X(jω)$ 与 $e^{-jωt_0}$ 相乘相当于是幅度不变，但是相位改变（即旋转）。而且还不仅仅于此，我们看 $e^{-jωt_0}$，如果 $ω >0$ 相当于把频谱按顺时针旋转。 $ω < 0$相当于把频谱往逆时针旋转。

我们下面举一个Matlab仿真的实例来直观地理解——“时域延迟等价于频谱旋转”这句话：
我们考虑两个非周期矩形信号，第一个的幅度是1，脉冲宽度也是1. 第二个信号和第一个是一样的，只不过是延迟了 0.1s 的信号。我们来看看它们的频谱。

我们根据前面的知识知道，幅度是1，脉冲宽度也是1的非周期矩形信号的频谱是 $sinc(f)$。因此：

f=-4:0.001:4;
X=sinc(f);
xlabel('x');
ylabel('f');
zlabel('y');
plot3(X,f,0*f);
grid on;
line([0 0],[-4 4],[0 0]);
axis([-1.5 1.5 -4 4 -1.5 1.5]);
set(gca,'YDir','reverse');

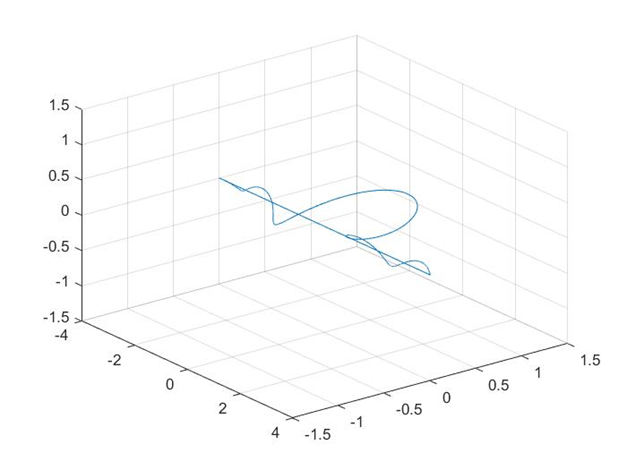
对于第二个信号，因为是延迟了0.1s，因此频谱需要乘上 $e^{-jω0.1}$

figure(2);
f=-4:0.001:4;
t0=0.1;
X=sinc(f).*exp(-i*2*pi*f*t0);
x=real(X);
y=imag(X);
xlabel('x');
ylabel('f');
zlabel('y');
plot3(x,f,y);
grid on;
line([0 0],[-4 4],[0 0]);
axis([-1.5 1.5 -4 4 -1.5 1.5]);
set(gca,'YDir','reverse');

通过上面两幅立体图的比较我们确实发现：在 $f >0$ 时，频谱是朝着顺时针去旋转的；在 $f <0$ 时，频谱是朝着逆时针去旋转的。

在和老师进行了一番讨论之后，我们有了下面的解释：
对于连续时间非周期信号的时移，我们认为：频谱幅度保持不变；但是相位谱发生了改变。

3. 频移 —— 频谱搬移问题

我们先给出结论：若： $x(t) \space \underleftrightarrow{\mathscr{F}} \space X(jω)$，那么有： $x(t)e^{jω_0t} \space \underleftrightarrow{\mathscr{F}} \space X(j(ω-ω_0))$
这里我们可以理解为：时域的旋转等价于频谱的平移。在个性质的用途在 $IQ$ 调制里面经常使用，我们看：

比如设我们的 I 路信号是 $x(t)$，那么根据 $IQ$ 调制，我们需要把 $I$ 路信号和 $cos(ω_0t)$ 相乘： $\mathscr{F}[x(t)cos(ω_0t)] = \mathscr{F}[\frac{1}{2}x(t)e^{jω_0t} + \frac{1}{2}x(t)e^{-jω_0t}]$
根据傅里叶变换的线性，我们又可以得到： $\mathscr{F}[\frac{1}{2}x(t)e^{jω_0t} + \frac{1}{2}x(t)e^{-jω_0t}] = \frac{1}{2} \mathscr{F}[x(t)e^{jω_0t}] + \frac{1}{2} \mathscr{F}[x(t)e^{-jω_0t}]$
那么这样一来，每一项都可以看成是 $x(t)$ 的旋转（ $ω_0 >0$是顺时针旋转， $ω_0 < 0$是逆时针旋转），因此，我们就可以得出： $\mathscr{F}[x(t)cos(ω_0t)] = \frac{1}{2}X(j(ω-ω_0)) + \frac{1}{2}X(j(ω+ω_0))$
也就是说：信号 $x(t)$ 与 $cos(ω_0t)$ 相乘，相当于把原信号的频谱分别搬移到 $±ω_0$ 的地方，同时频谱的幅度还需要变为原来的一半！

扫描二维码关注公众号，回复： 11382491 查看本文章

4. 共轭对称性

单说性质的话其实和傅里叶级数的共轭对称性差不多，我们先来看看：
若： $x(t) \space \underleftrightarrow{\mathscr{F}} \space X(jω)$，那么则： $x^*(t) \space \underleftrightarrow{\mathscr{F}} \space X^*(-jω)$

下面给出证明： $\begin{aligned} X(jω) &= \int_{-∞}^{+∞}x(t)e^{-jωt}dt\\ \space\\ X^*(jω) &=[\int_{-∞}^{+∞}x(t)e^{-jωt}dt]^* = \int_{-∞}^{+∞}x^*(t)e^{jωt}dt\\ \end{aligned}$
下面我们令： $ω = -ω$，那么有： $X^*(-jω) = \int_{-∞}^{+∞}x^*(t)e^{-jωt}dt$
所以我们证明出了： $x^*(t)$ 的频谱就是 $X^*(-jω)$

4.1 当信号 x(t) 是实信号时频谱的实部虚部

我们先给出结论：如果 $x(t)$ 是实信号（即 $x(t) = x^*(t)$）那么， $x(t)$ 的频谱 $X(jω)$ 的实部是偶函数，虚部是奇函数。

对于 $X(jω)$ 有： $X(jω) = Re[X(jω)] + jIm[X(jω)]$
那么 $X^*(jω) = Re[X(jω)] - jIm[X(jω)]$
$X^*(-jω) = Re[X(-jω)] - jIm[X(-jω)]$
因为信号 $x^*(t)$ 的频谱是 $X^*(-jω)$，而对于实信号又有： $x(t) = x^*(t)$，所以我们得出： $X(jω) = X^*(-jω)$
因此，我们可以得到： $X(jω)$ 实部和虚部的关系： $Re[X(jω)] = Re[X(-jω)]\quad Im[X(jω)] = -Im[X(-jω)]$
因此，我们得出：如果 $x(t)$ 是实信号（即 $x(t) = x^*(t)$）那么， $x(t)$ 的频谱 $X(jω)$ 的实部是偶函数，虚部是奇函数。

4.2 当信号 x(t) 是实信号时频谱的幅值和相角

这里我们可以得到非常类似的结论：当信号 $x(t)$ 是实信号时， $X(jω)$ 的幅值偶函数，相角是奇函数。
（证明与4.1一样，这里不再赘述）

4.3 当信号 x(t) 是实偶信号或实奇信号时

和傅里叶级数的性质一样：

1. 当 $x(t)$ 是实偶信号时，其频谱 $X(jω)$ 也会是一个实偶函数。
2. 当 $x(t)$ 是实奇信号时，其频谱 $X(jω)$ 将会是一个虚奇函数。

4.4 实信号 x(t) 奇偶分解后对应的频谱

对于一个实信号 $x(t)$，如果我们将它按照奇偶成分分解，即： $x(t) = x_e(t) + x_o(t)$
其中 $x_e(t)$ 表示奇成分。
那么，信号 $x(t)$ 的频谱 $X(jω)$ 也可以拆分成对应的奇偶成分： $X(jω) = X_e(jω) + X_o(jω)$
而且，我们有： $x_e(t) \space \underleftrightarrow{\mathscr{F}} \space Re\{X(jω)\}$； $x_o(t) \space \underleftrightarrow{\mathscr{F}} \space jIm\{X(jω)\}$（注意有一个 “j” 别忘了！！）

5. 微分性和积分性

若： $x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω)$，那么我们有： $\frac{dx(t)}{dt} \space \underleftrightarrow{\mathscr{F}} \space X(jω)jω$
证明过程也很简单，这里不再赘述。

同理，我们也需要记住傅里叶变换的积分性： $\int_{-∞}^{t}x(τ)dτ \space \underleftrightarrow{\mathscr{F}} \space \frac{1}{jω}X(jω) + πX(0)δ(ω)$
在我们直接计算一个信号的频谱不太方便的时候，如果这个信号的微分刚好是某一个特别的信号，那么我们可以先计算这个微分的信号，然后我们看看这个微分的信号的频谱在 $ω = 0$的时候是否为0，最后带入傅里叶变换的积分特性就可以得到原信号 $x(t)$ 的频谱了。值得注意的是：我们在积分性公式里面的 $X(jω)$ 应该是 $x(t)$ 的微分信号的频谱。

6. 尺度变换

我们先给出结论： $x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω)$，那么我们有： $x(at)\space \underleftrightarrow{\mathscr{F}} \space \frac{1}{|a|}X(j\frac{ω}{a})$

下面证明一下： $\begin{aligned} \mathscr{F}[x(t)] &= \int_{-∞}^{+∞}x(t)e^{-jωt}dt\\ \space\\ \mathscr{F}[x(at)] &= \int_{-∞}^{+∞}x(at)e^{-jωt}dt\\ \end{aligned}$
下面我们令 $y = at$，则上式变为： $\begin{aligned} \mathscr{F}[x(at)] &= \int_{-∞}^{+∞}x(at)e^{-jωt}dt\\ &=\int_{-∞}^{+∞}x(y)e^{-jω\frac{y}{a}}d(\frac{y}{a}) \end{aligned}$
下面我们需要对 $a$ 的正负分情况讨论，所以才会有后面的 $|a|$
【1】当 $a > 0$ 时， $\mathscr{F}[x(at)] =\frac{1}{a}\int_{-∞}^{+∞}x(y)e^{-jω\frac{y}{a}}dy$
此时， $x(at)$ 的频谱就是： $\frac{1}{a}X(j\frac{ω}{a})$
当 $a < 0$时， $x(at)$ 的频谱就是： $\frac{1}{-a}X(j\frac{ω}{a})$
因此，如果有： $x(t)\space \underleftrightarrow{\mathscr{F}} \space X(jω)$，那么我们有： $x(at)\space \underleftrightarrow{\mathscr{F}} \space \frac{1}{|a|}X(j\frac{ω}{a})$

7. 帕斯瓦尔定理

下面直接给出公式： $\int_{-∞}^{+∞}|x(t)|^2dt = \frac{1}{2π}\int_{-∞}^{+∞}|X(jω)|^2dω$
连续时间非周期信号的帕斯瓦尔定理建立了非周期信号能量与频谱能量的关系。

【傅里叶变换的性质表】

好啦，这就是本次 $Blog$ 的全部内容，我们在本文中介绍了傅里叶变换的几种基本性质——时移、反转、尺度变换、微分积分、频移、共轭对称还有帕斯瓦尔定理。但是值得注意的是，这还不全是傅里叶变换的性质，在后面的一篇 $Blog$ 里面，我们将详细地研究傅里叶变换与卷积的关系。see you！