
1 class Solution { 2 public int countOdds(int low, int high) { 3 if(low % 2 == 0 && high % 2 == 0) 4 return (high - low) / 2; 5 if(low % 2 != 0 && high % 2 !=0) 6 return (high - low) / 2 + 1; 7 return (high + 1 - low) / 2; 8 } 9 }
数学规律,送分题
1 class Solution { 2 public int numOfSubarrays(int[] arr) { 3 int res = 0; 4 int mod = 1000000007; //取余 5 int len = arr.length; 6 int[] count = new int[2]; //count[0]为偶数个数,count[1]为奇数个数 7 int[] sub = new int[len + 1]; //前缀和 8 sub[0] = arr[0]; 9 int[] dp = new int[len]; //记录前缀和奇偶性,1为奇,0为偶 10 if (sub[0] % 2 == 1) { 11 res = 1; 12 dp[0] = 1; 13 count[1] = 1; 14 } 15 else count[0] = 1; 16 if (len == 1) 17 return res; 18 for (int i = 1; i < len; i++) { 19 sub[i] = sub[i-1] + arr[i]; //计算前缀和 20 if(sub[i] % 2 == 1) { //前缀和为奇数 21 res += 1; //结果+1 22 dp[i] = 1; //置位1表示为奇数 23 count[1]++; //奇数前缀和数量+1 24 } 25 else { //结果为偶 26 dp[i] = 0; //置位0表示为偶 27 count[0]++; //偶数前缀和+1 28 } 29 res = (res +count[1 - dp[i]]) % mod; //通过奇-偶=奇,偶-奇=奇,统计所有奇数数组 30 } 31 return res; 32 } 33 }
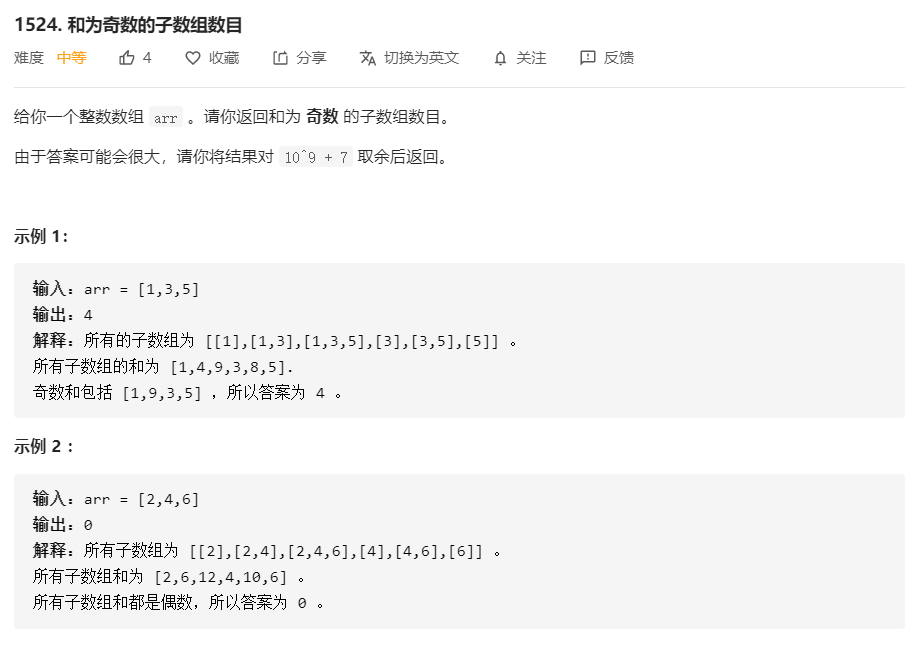
解题思路:
对于该类,将数组分为连续的数组,求其和的题目,都可使用前缀和来进行解答。该题也是如此,先利用前缀和记录数组的所有前缀和。由于题目要求寻找和为奇数的子数组数目,如果我们继续遍历数组,利用前缀和相减的方式求出所有的子数组之和,那么这种暴力法将会超时,所以要进行优化。根据数学规律,不难发现,只有偶数-奇数,奇数-偶数时,才会得到奇数解,那么我们可以利用这个规律,创建一个新的dp数组,来存储[0,len - 1]的所有前缀和的奇偶性。
那么我们就只需要,寻找与当前奇偶性相反的前缀和,就能匹配出新的和为奇数的子数组,那么如何寻找这些前缀和呢?显然,每次都再次遍历数组,那么时间复杂度将会大大增加,依旧没有达到优化的效果。那么我们继续优化,既然题目只需要寻找子数组的个数,那么我们是否可以创建一个数组,来存储前缀和奇数的个数,以及偶数的个数呢?当然是可以的,于是定义一个数组count[2],count[0]为偶数前缀和的个数,count[1]为奇数前缀和的个数,遍历时只需要加上count[1 - dp[i]]就是当前的奇数数组了。
注意点:
当计算前缀和为奇数时,res需要进行+1操作,因为这也是一个可能的子数组。
进行前缀和计算时,可以先计算arr[0]的情况,防止计算前缀和时下标越界;当然也可以将sub数组,dp数组都定义成len + 1的长度。
时间复杂度:O(N),N为数组长度
空间复杂度:O(N)
1 class Solution { 2 public int numSplits(String s) { 3 int res = 0; 4 int len = s.length(); 5 if (len == 1) 6 return res; 7 int[] dpLeft = new int[len]; //从左往右读的不同字符数目 8 int[] dpRight = new int[len]; //从右往左读的不同字符数目 9 dpLeft[0] = 1; //边界设置 10 dpRight[len - 1] = 1; 11 HashMap<Character, Integer> left = new HashMap<Character, Integer>(); //存储从左往右读的字符 12 left.put(s.charAt(0), 1); 13 for (int i = 1; i < len; i++) { //从左往右读取字符 14 if (!left.containsKey(s.charAt(i))) { //判断是否重复,不重复,字符数目+1,字符存入哈希表,方便后续判断是否重复 15 dpLeft[i] = dpLeft[i-1] + 1; 16 left.put(s.charAt(i), 1); 17 } 18 else dpLeft[i] = dpLeft[i - 1]; //字符重复,数目不变 19 } 20 HashMap<Character, Integer> right = new HashMap<Character, Integer>(); //存储从右往左读的字符 21 right.put(s.charAt(len - 1), 1); 22 for (int j = len - 2; j >= 0; j--) { //从右往左读取字符 23 if (!right.containsKey(s.charAt(j))) { //判断是否重复,与从左往右读操作一致 24 dpRight[j] = dpRight[j+1] + 1; 25 right.put(s.charAt(j), 1); 26 } 27 else dpRight[j] = dpRight[j + 1]; 28 } 29 for (int i = 0; i < len - 1; i++) { //遍历判断从左往右读的字符数是否等于从右往左读的字符数 30 if (dpLeft[i] == dpRight[i + 1]) 31 res++; //统计结果 32 } 33 return res; 34 } 35 }
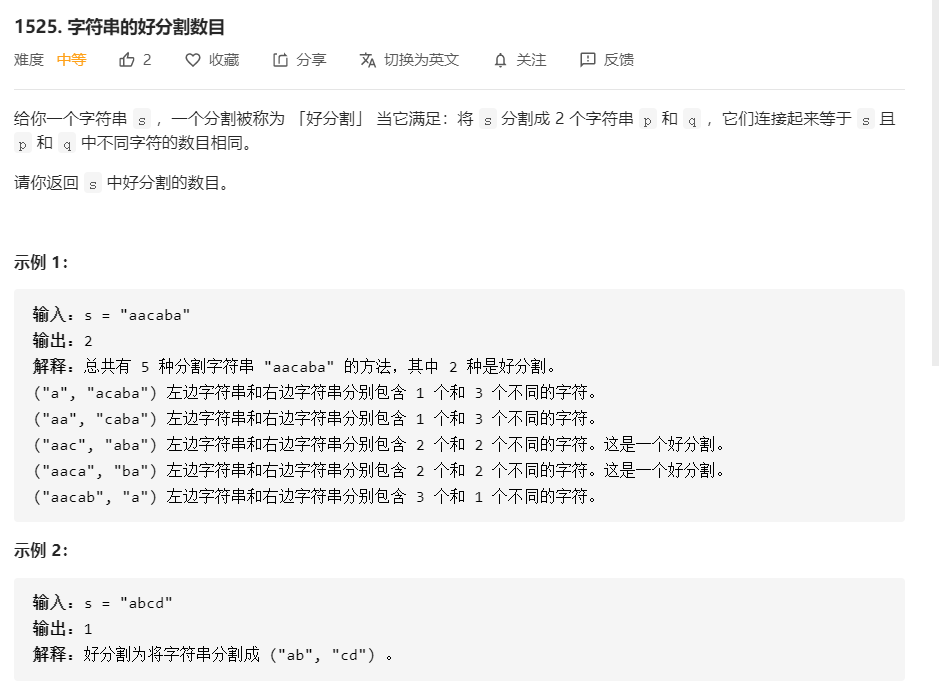
解题思路:
根据题目要求,可以使用暴力法的方式解答,遍历所有可能的分割情况,判断其是否符合要求;当然,这种暴力法并不可取,时间复杂度太高。我们需对其进行优化,由于是将字符串一分为二来进行字符数的统计,那么关键就是在于这两部分的字符数量如何快速的计算,我们先看左半部分,不难发现,我们只需遍历一次数组,就可以将左半部所有可能的情况计算出来,那么对应的右半部如何计算呢?其实,右半部与左半部是等价的,如果我们将字符串颠倒,那么右半部就是新的左半部,就也同样只需遍历一次就可以求出所有的情况。所以对于右半部来说,我们只需从尾部出发,反向遍历数组就可以求出其所有情况了。最后只需找出对应的左右字符数是否相等即可。
注意点:
由于需要就算字符数,那么重复的字符就需去除,此处可以采用哈希表来进行存储,达到去重的目的。
最后匹配计算时,由于左右两部分中间是相邻的两个数字,而非重合。也就是对应数组应该为dpLeft[i]与dpRight[i + 1]
时间复杂度:O(N),N为字符串长度
空间复杂度:O(N)
1 class Solution { 2 public int minNumberOperations(int[] target) { 3 int res = 1; 4 int len = target.length; 5 res = target[0]; 6 for (int i = 1; i < len; i++) { 7 if (target[i] > target[i - 1]) 8 res += target[i] - target[i - 1]; 9 } 10 return res; 11 } 12 }
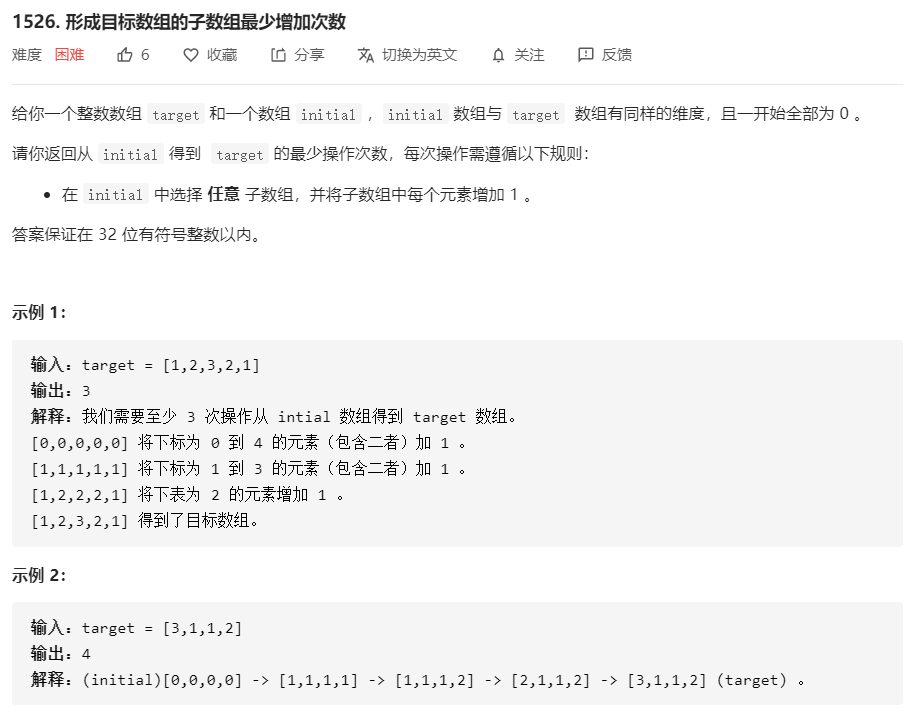
解题思路:
不是很好证明,有一点单调递增栈的意味。简单说明就是,只可以选择子数组进行-1操作,那么这段连续数字的子数组,都变为0,就取决于其最大值。