matlab根据转移函数绘制放大器幅频响应和相频响应

**

康华光-《电子学技术基础-模拟部分》第367页

**

(1)增加主极点
在反馈环路中增加一个主极点(参见图 7.9.2) ,并使它远离第二个极点,从而改变环路增益的频率特性,实现频率补偿。
例 7.8.1
设一电压放大电路的开环电压增益表达式为

$\dot{A}_{v}=\frac{10^{5}}{\left(1+\mathrm{j} f / 10^{5}\right)\left(1+\mathrm{j} f / 10^{6}\right)\left(1+\mathrm{j} f / 10^{7}\right)}$
式中 $10^5$是低频电压增益。 $\dot{A}_{v}$ 的频率响应波特图如图 7.8.4 所示,其主极点频率是 $10^5$Hz 。将它组成负反馈放大电路,反馈网络由纯电阻组成,反馈系数 $F_v=0.02$试分析该电路的工作稳定性,若不稳定,请用增加主极点的方法,
实现频率补偿。
书上的图是这样的，上面的转移函数对应下面波特图中的红线。

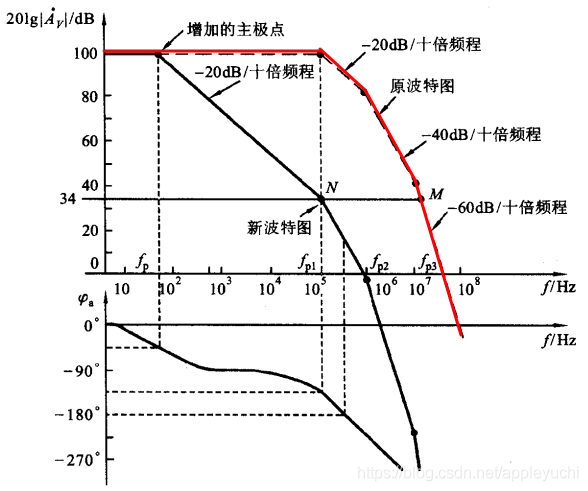
我们尝试用matlab代码来实现
首先转化上述式子:
$jf=\frac{s}{2\pi}$
所以上述式子转化为:

$\dot{A}_{v}=\frac{10^{5}}{\left(1+\mathrm{j} f / 10^{5}\right)\left(1+\mathrm{j} f / 10^{6}\right)\left(1+\mathrm{j} f / 10^{7}\right)}$

三个极点:

$z_1=-2π*10^5$
$z_2=-2π*10^6$
$z_3=-2π*10^7$
所以
$\dot{A}_{v}=\frac{10^{23}(2π)^3}{(z+z_1)(z+z_2)(z+z_3)}$
Matlab代码如下:

z=[]'
p=[-2*pi*10^5 -2*pi*10^6 -2*pi*10^7]'
k=10^23*(2*pi)^3

[num,den]=zp2tf(z,p,k)
P=bodeoptions;
P.FreqUnits='Hz';

g=tf(num,den)
bode(g,P)

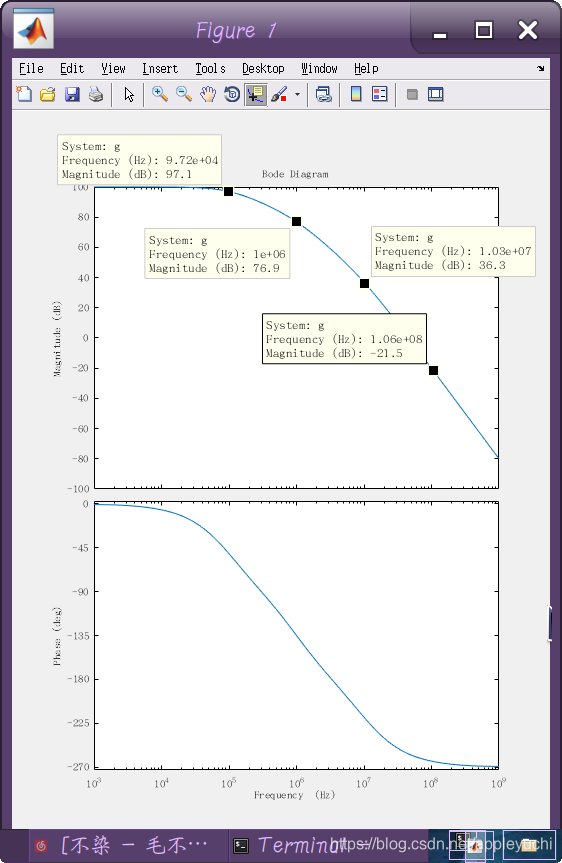
根据上面读数可以看出，每经过一个极点，幅频下降斜率就会增加约
-20db/10倍频
因此可以验证书上的幅频图是正确的。

这里写matlab的时候需要注意两点:
①虽然代码中把频率单位调整为Hz，
但是输入的频率依然是角频率w，而不是 $f$
②调整单位后，matlab已经自动帮你计算了 $20log|\dot{A}_{v}|$
可以看到幅频图低通区域数值是100dB,与书上完全一致。