我们都知道在pytorch中的nn.Linear表示线性变换,官方文档给出的数学计算公式是 y = xA^T + b,其中x是输入,A是权值,b是偏置,y是输出,卷积神经网络中的全连接层需要调用nn.Linear就可以实现。而在看pytorch的源码linear.py文件时可以看到里面有Bilinear的定义,起初看到这个名字,大家会以为它是实现对图像做放大的上采样插值,可是在pytorch中有nn.Upsample模块是对图像做上采样的。于是看linear.py文件中对Bilinear的定义,如下图所示

可以看到它的数学计算公式是y = x1 * A * x2 + b,不过里面关于shape的说明,讲的含糊不清。为了弄懂Bilinear的计算过程,我们按照文档给出的例子运行一次nn.Bilinear的计算,然后把两个输入input1和input2,以及weight和bias都转换成numpy.array的形式,然后用numpy函数实现一次Bilinear的计算,把最后的输出结果跟nn.Bilinear的计算输出结果求误差值,代码如下:
print('learn nn.Bilinear')
m = nn.Bilinear(20, 30, 40)
input1 = torch.randn(128, 20)
input2 = torch.randn(128, 30)
output = m(input1, input2)
print(output.size())
arr_output = output.data.cpu().numpy()
weight = m.weight.data.cpu().numpy()
bias = m.bias.data.cpu().numpy()
x1 = input1.data.cpu().numpy()
x2 = input2.data.cpu().numpy()
print(x1.shape,weight.shape,x2.shape,bias.shape)
y = np.zeros((x1.shape[0],weight.shape[0]))
for k in range(weight.shape[0]):
buff = np.dot(x1, weight[k])
buff = buff * x2
buff = np.sum(buff,axis=1)
y[:,k] = buff
y += bias
dif = y - arr_output
print(np.mean(np.abs(dif.flatten())))最后的运行结果是:
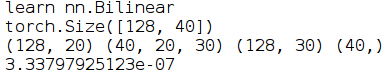
可以看到我们自己用numpy实现的Bilinear跟调用pytorch的Bilinear的输出结果的误差在小数点后7位,通过编写这个程序,现在可以理解Bilinear的计算过程了。需要注意的是Bilinear的weight是一个3维矩阵,这是跟nn.linear的一个最大区别。
首先,以weight的第0维开始,逐个遍历weight的每一页,当遍历到第k页时,输入x1与weight[k,:,:]做矩阵乘法得到buff,然后buff与输入x2做矩阵点乘得到新的buff,接下来对buff在第1个维度,即按行求和得到新的buff,这时把buff的值赋值给输出y的第k列
遍历完weight的每一页之后,加上偏置项,这时候Bilinear的计算就完成了。为了检验编写的numpy程序是否正确,我们把输出y跟调用pytorch的nn.Bilinear得到的输出output转成numpy形式的arr_output做误差比较。
我们在学习深度学习算法时,需要理解一个深度神经网络里的每种类型的层的计算原理,比如卷积层,池化层,以及在这篇文章里讲到的nn.Bilinear双线性变换层,而不能仅仅只是学会调用一个深度学习框架的接口函数就觉得已经掌握了深度学习算法。为了弄懂神经网络中的一个层的计算原理,比如pytorch框架里的nn.Module和nn.functional模块里的函数,我们可以把张量数据转换成numpy形式的数据,然后用numpy函数实现这个功能,最后把输出结果跟调用pytorch的输出结果做误差比较,这样有利于对深度学习算法的实现原理的理解