【数据结构】BIT树状数组详解——【单点更新+区间查询】【区间更新+单点查询】【区间更新+区间查询】【多维树状数组】

前言

我觉得这篇文章应该算是介绍的比较全面了，将树状数组的常用情况和推广都收集学习了一下，希望对大家有所帮助。

树状数组介绍

树状数组是由线段树修改而来，通过去掉不必要的节点从而简化空间结构，且更便于实现及使用。

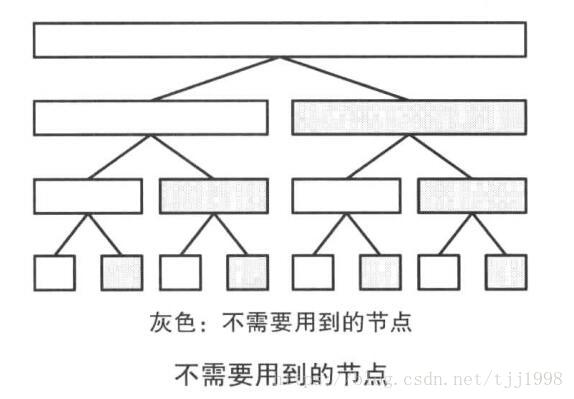
举个例子，如果我们要计算3-7区间的和，线段树可以直接通过（3-4）+（5-6）+（7）解决，而BIT则通过（1-4）+（5-6）+（7）-（1-2）-（3）解决，即需要计算两次的和，相当于用时间去换内存，不过由于求和的复杂度为O(logn)，所以我觉得是十分方便的。

树状数组应用

树状数组用于解决以下问题：
1.对一个位置进行修改并快速查询一段区间和的问题
2.对一段区间进行修改并快速查询一个位置的问题
3.对于一段区间进行修改并快速查询一段区间的问题

三种树状数组的基本操作都是一样的，不过所保存的信息不同，后续会补上另外两个的

树状数组实现

lowbit函数：用于寻找x转换为二进制后的最后一个1的位置:10(1010)为2，8(1000)为8。
原理：-x是用补码处理，1010的补码为0101+1=0110（省略了符号位），+1将所有末尾的1置为0，将最后一个0变为1，由于转成反码后0的位置为之前1的位置，所以原码和补码之间只有这一位是相同的，所以x&(-x)为x转换为二进制后的最后一个1的位置。关于有什么用这个问题，后面用到时会解释。

int lowbit(ll x){
    return x&(-x);  
}

add函数： 所有包含k这个位置的数组值加上data，假设add(5，1)，N为20，那么需要更新的位置为5(00101)，6(00110)，8(01000)，16(10000)；add(10,1)，那么需要更新的位置为10(01010)，12(01100)，16(10000)。通过规律我们可以发现，每次更新都是把当前最低位的1加上1。

解释(自己写的，其实不理解死记也行)：

由于我们的设定，2(10)管的是01和10，12(1100)管的是1001到1100，即从去掉最低位的1后+1的值到其本身，所以奇数代表其本身的值。
只有后面的更新的数最低位的1都高于当前的数，去掉末尾1后才能小于当前的数，所以一直加上最末尾的1的值，直到大于N为止。
举个例子，11(01011),最后一位加上1后变成12(01100)，再加上1后变成16(10000)，为什么14不算呢，因为14(01110)最低位的1是2，去掉末尾1再+1为13，起始数大于11了。

void add(int k,int data){//单点修改 
    while(k<=N){
        BIT[k]+=data;
        k+=lowbit(k);
    }
}

求前k项和： 与加相反，每次减去最低位的1，这个应该比较好理解，比如15(1111)，求和就是(1-8)+(9-12)+(13-14)+15；11(1011)，求和就是(1-8)+(9-10)+11。

ll sum(ll k){//求前k项和 
    ll Sum=0;
    while(k>0){
        Sum+=BIT[k];
        k-=lowbit(k);   
    }
    return Sum;
} 

单点更新+区间查询：

该类型中，每个位置保存的为区间（a，b）的和，前面就是按照这种情况解释的。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<ctime>
#define INF 99999999
#define bug puts("Hello\n")
#define MAX_N 1000010
#define ll long long int
using namespace std;
ll BIT[MAX_N]; 
int N;
ll lowbit(ll x){//寻找最小的1的位置,核心代码 
    return x&(-x);  
}
void print(){//输出BIT 
    for(long long int i=1;i<=N;i++){
        printf("%lld(%lld-%lld) ",BIT[i],i-lowbit(i)+1,i); 
    }
    printf("\n");
} 
void add(int k,int data){//单点修改 
    while(k<=N){
        BIT[k]+=data;
        k+=lowbit(k);
    }
}
ll sum(ll k){//求前k项和 
    ll Sum=0;
    while(k>0){
        Sum+=BIT[k];
        k-=lowbit(k);   
    }
    return Sum;
} 
int main(){
    srand(time(0));
    N=10;
    for(int i=1;i<=10;i++){
        add(i,i);
        print();
    }
    for(int i=0;i<10;i++){
        ll x2=0;
        while(x2==0)x2=rand()%9+2;      
        ll x1=0;
        while(x1==0)x1=rand()%x2;
        printf("%lld %lld\n",x1,x2);
        printf("%lld\n",sum(x2)-sum(x1-1));
    }
    return 0;
}

区间更新+单点查询：

该类型中，保存的为差分数组An-An-1（An为数列中第n项），所以第k位保存的为Ak-Ak-1这个数组从(a-k)的和，举个例子，6保存的为(5,6)的值，也就是A6-A4。
为什么会这样保存：
因为我们要处理的是区间更新。（这算啥- -，继续往下看吧，请忽略这句话）
这样保存的结果是：
我们所求的单点An的值，为前n项和(这个应该可以理解吧)。
这样保存的好处是：
我们只需要给Ai+data，那么所有的比i大的项都会加data。（根据前面的单点更新理解。）

扫描二维码关注公众号，回复： 1434141 查看本文章

所以如果我们需要给(a,b)区间的数加上data，我们只需要add(a,data)，add(b+1,-data)。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<ctime>
#define INF 99999999
#define bug puts("Hello\n")
#define MAX_N 1000010
#define ll long long int
using namespace std;
ll BIT[MAX_N]; 
int N;
ll lowbit(ll x){//寻找最小的1的位置,核心代码 
    return x&(-x);  
}
void add(int k,int data){//单点修改 
    while(k<=N){
        BIT[k]+=data;
        k+=lowbit(k);
    }
}
ll sum(ll k){//求前k项和 
    ll Sum=0;
    while(k>0){
        Sum+=BIT[k];
        k-=lowbit(k);   
    }
    return Sum;
} 
void print(){//输出BIT 
    for(long long int i=1;i<=N;i++){
        printf("%lld(%lld-%lld) ",BIT[i],i-lowbit(i)+1,i); 
    }
    printf("\n");
    printf("更新后结果：\n") ;
    for(long long int i=1;i<=N;i++){
        printf("%lld(%lld) ",sum(i),i); 
    }
    printf("\n\n"); 
} 
int main(){
    srand(time(0));
    N=10;
    for(int i=1;i<=10;i++){
        printf("1到%d加1：\n",i); 
        add(1,1);
        add(i+1,-1);
        print();
    }
    for(int i=0;i<10;i++){
        ll x1=0;
        while(x1==0)x1=rand()%9+2;      
        printf("%lld %lld\n",x1,sum(x1));
    }
    return 0;
}

区间更新+区间查询

这个是根据一个求和推导。
根据前面的区间更新+单点查询，我们知道An=∑di (i=1-n)，即di的前n项和，那么An的前n项和呢？
根据计算我们可以知道，有n个d1，n-1个d2，n-2个d3，…，直到1个dn，即(n-i+1)*di的前n项和，i从1-n
那么根据求和的性质，我们可以将这个求和公式拆成两个，一个是(n+1)di的前n项和，一个是i*di的前n项和。这样我们就可以通过维护两个树状数组来解决，一个维护di，一个维护i * di。

解释的还是比较丑陋，所以大家可以到https://blog.csdn.net/zars19/article/details/54620021 中的区间修改+区间查询部分查看那个推导过程和实例代码。

多维树状数组

用法跟一维树状数组相同，因为每个维度都是独立的，A[6][6] 中第一维保存的是a[5]+a[6]，第二维保存的分别是a[5][5]+a[5][6]，a[6][5]+a[6][6]。
如果需要求A[6][6]的和，则需要A[4][4]+A[4][6]，A[6][4]+A[6][6]，由此可见，我们只需要在一维外面套个循环，就可以实现二维了。
定义：

ll BIT[MAX_N][MAX_N]; 

更新：add函数

void add(int a,int b,int data){
    while(a<=N){
        while(b<=N){
            BIT[a][b]+=data;
            b+=lowbit(b);
        }
        a+=lowbit(a);
    }
}

求和：sum函数

ll sum(ll a,llb){
    ll Sum=0;
    while(a>0){
        while(b>0){
            Sum+=BIT[a][b];
            k-=lowbit(b);   
        }
        a+=lowbit(a);
    }
    return Sum;
}