《统计学习方法（第2版）》李航 第20章 潜在狄利克雷分配 LDA Dirichlet 思维导图笔记 及 课后全部习题答案（步骤详细， 包含吉布斯抽样算法）狄利克雷分布期望推导

思维导图：

20.1

推导狄利克雷分布数学期望公式。

首先写出Dirichlet分布的概率密度函数：
$$\rho (\theta )=\frac{\Gamma \left({\alpha }_0\right)}{\Gamma \left({\alpha }_1\right)\cdots P\left({\alpha }_n\right)}\prod _{i=1}^n{\theta }_i^{{\alpha }_i-1}$$
其中，${\alpha }_0={\sum }_{i=1}^n{a}_i$，那么期望值为：
$$\begin{array}{rl}E\left({\theta }_i\right)& =\int {\theta }_i\rho (\theta )d\theta \\ & =\int \frac{\Gamma \left({\alpha }_0\right)}{\Gamma \left({\alpha }_1\right)\cdots \Gamma \left({\alpha }_n\right)}{\theta }_i^{{\alpha }_i}\prod _{j\ne i}^n{\theta }_i{}^{{\alpha }_i-1}d\theta \end{array}$$
令：${\beta }_i={\alpha }_i+1,{\beta }_j={\alpha }_j,{\beta }_0=1+\Sigma {\alpha }_k=1+{\alpha }_0$，并利用$\Gamma (x+1)=x\Gamma (x)$，从而得到：
$$\begin{array}{lc}E\left({\theta }_i\right)& =\int \frac{{\alpha }_i}{{\alpha }_0}\frac{\Gamma \left({\beta }_0\right)}{\Gamma \left({\beta }_1\right)\cdots \Gamma \left({\beta }_n\right)}{\theta }_i^{{\beta }_i-1}{\prod }_{j\ne i}^n{\theta }_j^{{\beta }_j-1}d\theta \\ & =\frac{{\alpha }_i}{{\alpha }_0}\int \frac{\Gamma \left({\beta }_0\right)}{\Gamma \left({\beta }_1\right)\cdots \Gamma \left({\beta }_n\right)}{\prod }_{i=1}^n{\theta }_j^{{\beta }_j-1}d\theta \\ & =\frac{{\alpha }_i}{{\alpha }_0}\end{array}$$
倒数第二个等号，可以发现，整个积分是对于一个新的Dirichlet分布的积分，因此为1.
这就是书中(20.31)和(20.33)用的结论。

20.2

针对17.2.2的文本例子，用LDA模型进行话题分析。

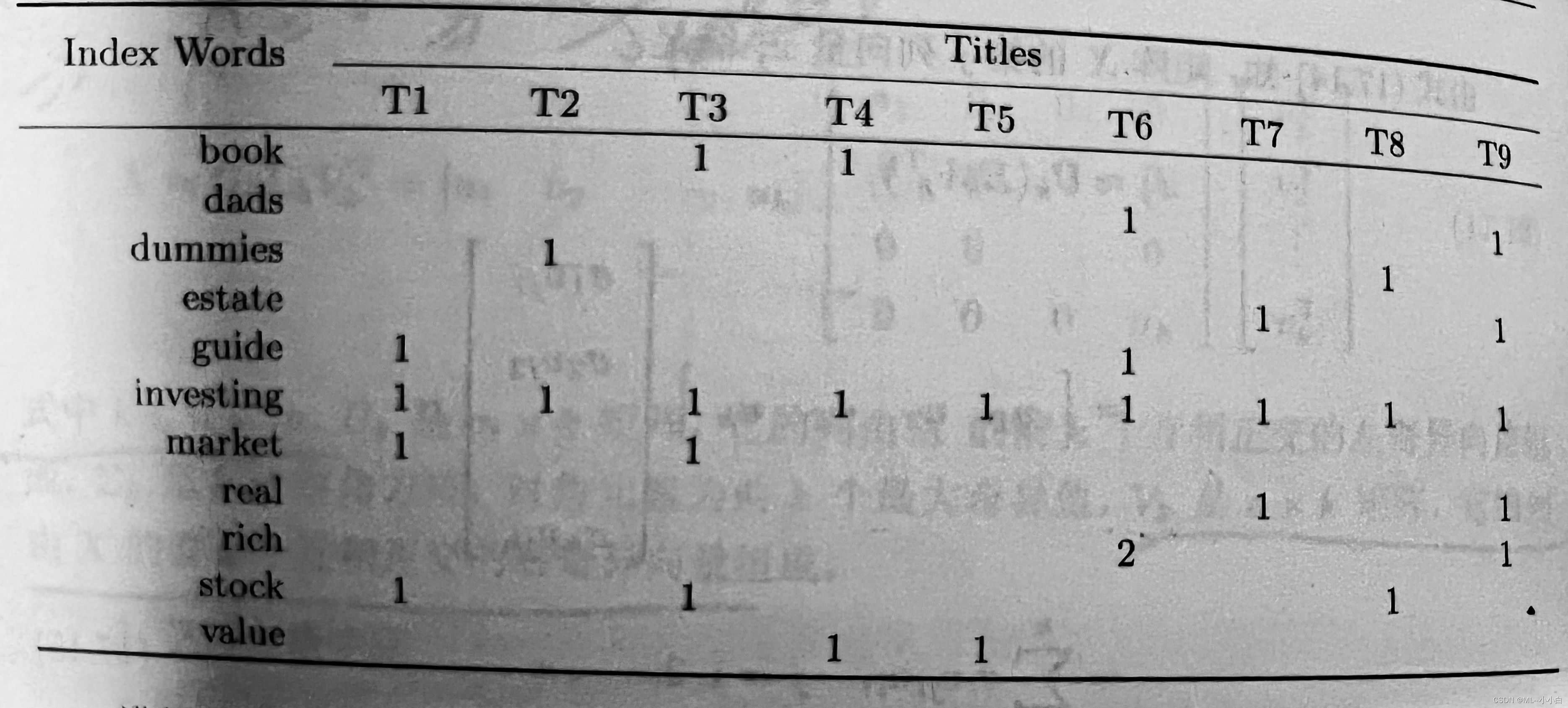
# 简单起见，利用吉布斯抽样，根据书中例子去了3个话题，这里也取3个

import numpy as np

np.random.seed(229)

# 文本的词汇序列
D = [[4, 5, 6, 9],
     [2, 5],
     [0, 5, 6, 9],
     [0, 5, 10],
     [5, 10],
     [1, 4, 5, 8, 8],
     [3, 5, 7],
     [2, 5, 9],
     [1, 3, 5, 7, 8]]
K = 3
V = 11
M = len(D)
# 没有先验的情况下，设置超参数分量均为1
alpha = np.ones(K)
# alpha = np.abs(np.random.randn(K))
# alpha = np.array([3.91, 2.61, 2])
beta = np.ones(V)
# beta = np.abs(np.random.randn(V))

# 初始化
topic_word = np.zeros((K, V))
document_topic = np.zeros((M, K))
topic_list = []
for m, document in enumerate(D):
    topics = []
    for word in document:
        topic = np.random.randint(0, K)
        document_topic[m, topic] += 1
        topic_word[topic, word] += 1
        topics.append(topic)
    topic_list.append(topics)
    
# 吉布斯抽样
# S = 2000  # 迭代次数
burning_cycle = 10000 # 燃烧期迭代次数
for it in range(burning_cycle):
    old_document_topic = document_topic.copy()
    for m, document in enumerate(D):
        for idx, word in enumerate(document):
            topic = topic_list[m][idx]
            document_topic[m, topic] -= 1
            topic_word[topic, word] -= 1
            word_prob = (topic_word[:, word] + beta[word]) / (topic_word + beta).sum(axis=1)
            topic_prob = (document_topic[m, :] + alpha) / (document_topic[m, :] + alpha).sum()
            topic_cond_prob = word_prob * topic_prob
            topic_cond_prob = topic_cond_prob / topic_cond_prob.sum()
            new_topic = np.random.choice([x for x in range(K)], p=topic_cond_prob)
            topic_list[m][idx] = new_topic
            document_topic[m, new_topic] += 1
            topic_word[new_topic, word] += 1
    loss = ((np.abs(document_topic) - np.abs(old_document_topic))**2).sum()
    if it % 1000 == 0:
        print(f'iteration {
      
      it}, loss: {
      
      loss}')
# 模型参数
phi = np.zeros((K, V))
theta = np.zeros((M, K))
for m in range(M):
    for k in range(K):
        theta[m, k] = document_topic[m, k] + alpha[k]
theta = theta / theta.sum(axis=1)[:, np.newaxis]
for k in range(K):
    for v in range(V):
        phi[k, v] = topic_word[k, v] + beta[v]
phi = phi / phi.sum(axis=1)[:, np.newaxis]
print(f'document-topic multinomial parameters:\n {
      
      theta}\n topic-word multinomial parameters:\n{
      
      phi}')

iteration 0, loss: 40.0
iteration 1000, loss: 44.0
iteration 2000, loss: 16.0
iteration 3000, loss: 38.0
iteration 4000, loss: 16.0
iteration 5000, loss: 54.0
iteration 6000, loss: 18.0
iteration 7000, loss: 70.0
iteration 8000, loss: 96.0
iteration 9000, loss: 44.0
document-topic multinomial parameters:
 [[0.14285714 0.42857143 0.42857143]
 [0.6        0.2        0.2       ]
 [0.28571429 0.14285714 0.57142857]
 [0.16666667 0.33333333 0.5       ]
 [0.2        0.6        0.2       ]
 [0.25       0.125      0.625     ]
 [0.5        0.33333333 0.16666667]
 [0.5        0.33333333 0.16666667]
 [0.25       0.125      0.625     ]]
 topic-word multinomial parameters:
[[0.05       0.1        0.15       0.1        0.05       0.15
  0.1        0.1        0.1        0.05       0.05      ]
 [0.05555556 0.05555556 0.05555556 0.05555556 0.11111111 0.16666667
  0.11111111 0.05555556 0.05555556 0.11111111 0.16666667]
 [0.11538462 0.07692308 0.03846154 0.07692308 0.07692308 0.23076923
  0.03846154 0.07692308 0.11538462 0.11538462 0.03846154]]

效果不好有两个可能原因，一个是对于先验的狄利克雷分布的参数，没有取到比较好的状态；另一个是，每个文本的的词数过少，从而抽样过少。

20.3

找出LDA的吉布斯抽样算法、变分EM算法中利用到狄利克雷分布的部分，思考LDA中使用狄利克雷分布的重要性。

在Gibbs sampling中，计算抽样分布的时候，推导其表达式的时候用到了，最终体现在利用吉布斯抽样结果以后利用模型参数的后验分布的期望进行模型参数的估计上。倘若没有这个狄利克雷分布的引入，那么可能造成过拟合；
在变分EM算法中，在E步确定一个Q函数（CS229定义的Q函数）的近似的时候用到了狄利克雷分布，也是作为模型参数的先验分布而引入的，最终体现在证据下限ELBO的期望值计算中，用到了狄利克雷分布本身的性质，同样的如果不引入狄利克雷分布，相当于在书中例子的基础上又将文本-话题矩阵做了简化，从而使得认为话题和单词的先验分布都是均匀分布，将和概率潜在分布一样，可能出现过拟合。

20.4

给出LDA的吉布斯抽样的算法复杂度和变分EM算法的复杂度。

对于吉布斯抽样：算法复杂度有关的几个循环，文本数M、文本单词数N，话题数K，抽样次数S，最终为$O(MNKS)$。
对于变分EM算法：算法复杂度有关的几个循环，文本数M、文本单词数N，话题数K，迭代次数S，最终也为$O(MNKS)$。

20.5

证明变分EM算法收敛。

书第404页，公式(20.41)就已经是证明了，每一项的含义往前找找就知道了，证明每一步都单调递增，就证明了证据下界每一步都递增，那么等价于KL散度每一步都单调递减，所以总会收敛。

扫描二维码关注公众号，回复： 14389383 查看本文章