《统计学习方法（第2版）》李航 第18章 概率潜在语义分析 PLSA PLSI 思维导图笔记 及 课后习题答案（步骤详细， 包含生成模型，共现模型算法推导及实现）第十八章

思维导图：

18.1

证明生成模型与共现模型是等价的。

首先，注意到一个重要的假设，假设z给定的条件下，w与d相互是独立的，则：
$$P(w,z\mid d)=P(z\mid d)P(w\mid z,d)=P(z\mid d)P(w\mid z)$$
$$P(w,d\mid z)=P(w\mid d)P(d\mid z)$$
接着，写出生成模型：
$$\begin{array}{rl}P(w,d)& =P(d)P(w\mid d)\\ & =P(d)P(w\mid d)\\ & =p(d)\sum _{z}P(w,z\mid d)\\ & =P(d)\sum _{z}P(z\mid d)P(w\mid z)\end{array}$$
写出共现模型：
$$\begin{array}{rl}P(w,d)& =\sum _{z}P(w,d,z)\\ & =\sum _{z}P(z)P(w,d\mid z)\\ & =\sum _{z}P(z)P(w\mid z)P(d\mid z)\end{array}$$
通过上面等式，可以得到：
$$\begin{array}{rl}& \sum _{z}P(z)P(w\mid z)P(d\mid z)\\ & =\sum _{z}P(z)P(w,d\mid z)\\ & =\sum _{z}P(w,d,z)\\ & =\sum _{z}P(w,z\mid d)P(d)\\ & =P(d)\sum _{z}P(z\mid d)P(w\mid z)\end{array}$$
开头和结尾分别是共现模型与生成模型，因此而这等价。

18.2

推导共现模型的EM算法。

首先，采用CS229当中定义Q函数的方法，即Q函数为不完全数据的条件概率分布函数，E步就是更新该值；Q步是更新完全数据在该不完全条件概率下的期望，更新参数使期望最大，下面简要回顾一下EM算法，再推导生成和贡献模型的EM算法。\

EM算法推导概要

对于一般的，含有一个隐变量的问题，对数似然函数为：
$$\begin{array}{rl}\ell (\theta )& =\sum _{i=1}^m\log p(x;\theta )\\ & =\sum _{i=1}^m\log \sum _{z}p(x,z;\theta )\end{array}$$
其中m为样本数。
因为隐变量的存在，直接求最值求而不得，没有解析解，因此用最大似然估计，EM迭代求解，每次逼近最大似然的一个下界。
令$Q_i$为第i个样本对应隐变量$z_i$的某种分布函数，则似然函数可以写为：
$$\begin{array}{rl}\sum _i\log p\left(x^{(i)};\theta \right)& =\sum _i\log \sum _{z^{(i)}}p\left(x^{(i)},z^{(i)};\theta \right)\\ & =\sum _i\log \sum _{z^{(i)}}{Q}_i\left(z^{(i)}\right)\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{Q_i\left(z^{(i)}\right)}\\ & \ge \sum _i\sum _{z^{(i)}}{Q}_i\left(z^{(i)}\right)\log \frac{p\left(x^{(i)},z^{(i)};\theta \right)}{Q_i\left(z^{(i)}\right)}\end{array}$$
最后的不等号用到了Jensens不等式。
这样有了下界还不够，我们希望在参数的位置上，这个不等号下界刚好与似然函数相切，也就是不等号取等号的时候，根据Jensens不等式取等号条件，可知，必须有：
$$\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{Q_i\left(z^{(i)}\right)}=c$$
或者：
$$Q_i\left(z^{(i)}\right)\propto p\left(x^{(i)},z^{(i)};\theta \right)$$
而$Q_i$为一个分布，需满足${\sum }_z{Q}_i\left(z^{(i)}\right)=1$，从而可以取：
$$\begin{array}{rl}{Q}_i\left(z^{(i)}\right)& =\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{{\sum }_{z}p\left(x^{(i)},z;\theta \right)}\\ & =\frac{p\left(x^{(i)},z^{(i)};\theta \right)}{p\left(x^{(i)};\theta \right)}\\ & =p\left(z^{(i)}\mid x^{(i)};\theta \right)\end{array}$$
所以Q函数即为不完全数据的条件概率分布函数。
从而，E步：
$$Q_i\left(z^{(i)}\right):=p\left(z^{(i)}\mid x^{(i)};\theta \right)$$
Q步：
$$\theta :=\arg \underset{\theta }{\max }\sum _i\sum _{z^{(i)}}{Q}_i\left(z^{(i)}\right)\log \frac{p\left(x^{(i)},z^{(i)};\theta \right)}{Q_i\left(z^{(i)}\right)}$$

生成模型EM算法推导

对于生成模型，按照相似的步骤，首先可以得到：
$$\begin{array}{rl}\ell (\theta )& =\sum _{i=1}^M\sum _{j=1}^N\log p(w^{(i)},d^{(j)};\theta {)}^{n(w^{(i)},d^{(j)})}\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\log p(w^{(i)},d^{(j)};\theta )\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\log \sum _{k=1}^{K}p(w^{(i)},d^{(j)};\theta )\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\log \sum _{k=1}^K{Q}_k(z_k)\frac{p(w^{(i)},d^{(j)};\theta )}{Q_k(z_k)}\\ & \ge \sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^K{Q}_k(z_k)\log \frac{p(w^{(i)},d^{(j)};\theta )}{Q_k(z_k)}\end{array}$$
然后，相同的分析可得：
$$\begin{array}{rl}{Q}_k(z_k)& =\frac{p(w^{(i)},d^{(j)},z_k;\theta )}{{\sum }_{z}p(w^{(i)},d^{(j)},z;\theta )}\\ & =p(z_k|w^{(i)},d^{(j)};\theta )\end{array}$$
带回原来的极大似然函下界可得需要在Q步极大的目标函数$J$：
$$\begin{array}{rl}J& =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log \frac{p(w^{(i)},d^{(j)},z_k;\theta )}{p(z_k|w^{(i)},d^{(j)};\theta )}\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)},d^{(j)},z_k;\theta )\end{array}$$
其中第二行略去对数部分的分母是因为，其可以变成对数减法，之后因为这个Q在E步中更新，这里是定值，不进行更新，所以这项可以略去。
然后将生成模型套进来，根据上一题或者书本生成模型：$\begin{array}{rl}P(w,d)& =P(d)\sum _{z}P(z\mid d)P(w\mid z)=\sum _{z}P(z\mid d)P(w\mid z)P(d)\end{array}$，则可知：$P(w, d, z) = P(z \mid d) P(w \mid z) P(d) $从而：
$$\begin{array}{rl}J& =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)},d^{(j)},z_k;\theta )\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)}|z_k)p(z_k|d^{(j)})p(d^{(j)})\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)}|z_k)p(z_k|d^{(j)})\end{array}$$
其中对数中$p(d^{(j)})$因为可以直接通过统计得到，不需要更新获得，因此可以略去。
然后利用拉格朗日未定乘子法解出约束最优值。拉格朗日函数为：
$$\begin{array}{r}L=J+\alpha (1-\sum _{i=1}^{M}p(w^{(i)}|z_k))+\beta (1-\sum _{k=1}^{K}p(z_k|d^{(j)}))\end{array}$$
对其分别向$p(w^{(i)}|z_k)$和$p(z_k|d^{(j)})$求导得到：
$$\begin{array}{rl}\frac{\partial L}{\partial p(z_k|d^{(j)})}& =\frac{\partial J}{\partial p(z_k|d^{(j)})}-\alpha \\ & =\sum _{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})\frac{1}{p(z_k|d^{(j)})}-\alpha \end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial p(w^{(i)}|z_k)}& =\frac{\partial J}{\partial p(w^{(i)}|z_k)}-\beta \\ & =\sum _{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})\frac{1}{p(w^{(i)}|z_k)}-\beta \end{array}$$
分别令其为0，并分别对i，j求和，可以分别得到$\alpha$和$\beta$，带入可以得到：
$$\begin{array}{rl}p(w^{(i)}|z_k)& =\frac{{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{{\sum }_{i=1}^M{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}\end{array}$$
$$\begin{array}{rl}p(z_k|d^{(j)})& =\frac{{\sum }_{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{{\sum }_{k=1}^K{\sum }_{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}\\ & =\frac{{\sum }_{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{n(d^{(j)})}\end{array}$$
即，Q步中的更新规则。
而对于E步，需要用Q步中更新的参数进行更新，因此要做如下变形：
$$\begin{array}{rl}{Q}_k(z_k)& =p(z_k|w^{(i)},d^{(j)})\\ & =\frac{p(w^{(i)},d^{(j)}|z_k)p(z_k)}{{\sum }_l^{K}p(w^{(i)},d^{(j)}|z_l)p(z_l)}\\ & =\frac{p(w^{(i)}|z_k)p(d^{(j)}|z_k)p(z_k)}{{\sum }_l^{K}p(w^{(i)}|z_l)p(d^{(j)}|z_l)p(z_l)}\\ & =\frac{p(w^{(i)}|z_k)p(d^{(j)},z_k)}{{\sum }_l^{K}p(w^{(i)}|z_l)p(d^{(j)},z_l)}\\ & =\frac{p(w^{(i)}|z_k)p(z_k|d^{(j)})p(d^{(j)})}{{\sum }_l^{K}p(w^{(i)}|z_l)p(z_l|d^{(j)})p(d^{(j)})}\\ & =\frac{p(w^{(i)}|z_k)p(z_k|d^{(j)})}{{\sum }_l^{K}p(w^{(i)}|z_l)p(z_l|d^{(j)})}\end{array}$$
其中第二个等号是贝叶斯公式；第三个等号利用了z给定条件下，w与d条件独立假设；最后一个等号是因为分母求和与j指标无关，所以分子分母可以约掉$p(d^{(j)})$。

共现模型EM算法推导

前面的与生成模型的推导是相同的，从Q步极大的目标函数$J$开始：
$$\begin{array}{rl}J& =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log \frac{p(w^{(i)},d^{(j)},z_k;\theta )}{p(z_k|w^{(i)},d^{(j)};\theta )}\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)},d^{(j)},z_k;\theta )\end{array}$$
其中第二行略去对数部分的分母是因为，其可以变成对数减法，之后因为这个Q在E步中更新，这里是定值，不进行更新，所以这项可以略去。
然后将生成模型套进来，根据上一题或者书本生成模型：$\begin{array}{rl}P(w,d)& =\sum _{z}P(z)P(w\mid z)P(d\mid z)\end{array}$，则可知：$P(w, d, z) = P(z) P(w \mid z) P(d \mid z) $从而：
$$\begin{array}{rl}J& =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)},d^{(j)},z_k;\theta )\\ & =\sum _{i=1}^M\sum _{j=1}^{N}n(w^{(i)},d^{(j)})\sum _{k=1}^{K}p(z_k|w^{(i)},d^{(j)};\theta )\log p(w^{(i)}|z_k)p(d^{(j)}|z_k)p(z_k)\end{array}$$
然后利用拉格朗日未定乘子法解出约束最优值。拉格朗日函数为：
$$\begin{array}{r}L=J+\alpha (1-\sum _{k=1}^{K}p(z_k))+\beta (1-\sum _{i=1}^{M}p(w^{(i)}|z_k))+\gamma (1-\sum _{j=1}^{N}p(d^{(j)}|z_k))\end{array}$$
对其分别向$p(z_k)$和$p(w^{(i)}|z_k)$和$p(z_k|d^{(j)})$求导得到：
$$\begin{array}{rl}\frac{\partial L}{\partial p(z_k)}& =\frac{\partial J}{\partial p(z_k)}-\alpha \\ & =\sum _{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})\frac{1}{p(z_k)}-\alpha \end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial p(w^{(i)}|z_k)}& =\frac{\partial J}{\partial p(w^{(i)}|z_k)}-\beta \\ & =\sum _{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})\frac{1}{p(w^{(i)}|z_k)}-\beta \end{array}$$
$$\begin{array}{rl}\frac{\partial L}{\partial p(d^{(j)}|z_k)}& =\frac{\partial J}{\partial p(d^{(j)}|z_k}-\gamma \\ & =\sum _{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})\frac{1}{p(d^{(j)}|z_k)}-\gamma \end{array}$$
分别令其为0，并分别对k，i，j求和，可以分别得到$\alpha$和$\beta$和$\gamma$，带入可以得到：
$$\begin{array}{rl}p(z_k)& =\frac{{\sum }_{i=1}^M{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{{\sum }_{k=1}^K{\sum }_{i=1}^M{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}\\ & =\frac{{\sum }_{i=1}^M{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{{\sum }_{j=1}^{N}n(d^{(j)})}\end{array}$$
$$\begin{array}{rl}p(w^{(i)}|z_k)& =\frac{{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{{\sum }_{i=1}^M{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}\end{array}$$
$$\begin{array}{rl}p(d^{(j)}|z_k)& =\frac{{\sum }_{i=1}^{M}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}{{\sum }_{i=1}^M{\sum }_{j=1}^{N}n(w^{(i)},d^{(j)})p(z_k|w^{(i)},d^{(j)})}\end{array}$$
此即，共现模型Q步中的更新规则。
而对于E步，需要用Q步中更新的参数进行更新，因此要做如下变形：
$$\begin{array}{rl}{Q}_k(z_k)& =p(z_k|w^{(i)},d^{(j)})\\ & =\frac{p(w^{(i)},d^{(j)}|z_k)p(z_k)}{{\sum }_l^{K}p(w^{(i)},d^{(j)}|z_l)p(z_l)}\\ & =\frac{p(w^{(i)}|z_k)p(d^{(j)}|z_k)p(z_k)}{{\sum }_l^{K}p(w^{(i)}|z_l)p(d^{(j)}|z_l)p(z_l)}\end{array}$$
其中第二个等号是贝叶斯公式；第三个等号利用了z给定条件下，w与d条件独立假设。

18.3

对以下文本数据集进行概率潜在语义分析。

import numpy as np

X = np.array([[0, 0, 1, 1, 0, 0, 0, 0, 0],
                  [0, 0, 0, 0, 0, 1, 0, 0, 1],
                  [0, 1, 0, 0, 0, 0, 0, 1, 0],
                  [0, 0, 0, 0, 0, 0, 1, 0, 1],
                  [1, 0, 0, 0, 0, 1, 0, 0, 0],
                  [1, 1, 1, 1, 1, 1, 1, 1, 1],
                  [1, 0, 0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 0, 0, 0, 0, 1, 0, 1],
                  [0, 0, 0, 0, 0, 2, 0, 0, 1],
                  [1, 0, 1, 0, 0, 0, 0, 1, 0],
                  [0, 0, 0, 1, 1, 0, 0, 0, 0]])

# 生成模型EM算法
def probabilistic_latent_semantic_analysis(data, topic_num=4, max_iter=11):
    word_num, document_num = X.shape
#     topic_num = 3
    # 初始化参数值
    word_top_prob = np.ones((word_num, topic_num)) / word_num
    top_doc_prob = np.ones((topic_num, document_num)) / topic_num
    # word_top_prob = np.random.rand(word_num, topic_num)
    # top_doc_prob = np.random.rand(topic_num, document_num)
    doc_prob = np.ones(document_num) / document_num
    # 迭代：
    it = 1
    print('===============生成模型结果===============')
    while it < max_iter:
        # E-step
        top_given_word_doc_prob = np.zeros((topic_num, word_num, document_num))
        for i in range(word_num):
            for j in range(document_num):
                top_given_word_doc_prob[:, i, j] = word_top_prob[i] * top_doc_prob[:, j] / (word_top_prob[i] @ top_doc_prob[:, j])
        # M-step
        old_word_top_prob = word_top_prob.copy()
        for i in range(word_num):
            for k in range(topic_num):
                word_top_prob[i, k] = X[i] @ top_given_word_doc_prob[k, i]
        word_top_prob = word_top_prob / word_top_prob.sum(axis=0)
        for k in range(topic_num):
            for j in range(document_num):
                top_doc_prob[k, j] = X[:, j] @ top_given_word_doc_prob[k, :, j]
        top_doc_prob = top_doc_prob / X.sum(axis=0)
        # 打印看是否有收敛趋势
        if it % 1 == 0:
            delta = np.abs(word_top_prob - old_word_top_prob).sum()
            print(f'variation: {
      
      delta}, iteration_num:{
      
      it}')
        it += 1
    print(f'文本概率为：\n{
      
      doc_prob}')
    print(f'已知话题，单词的条件概率矩阵为：\n{
      
      word_top_prob}')
    print(f'已知文本，话题的条件概率矩阵为：\n{
      
      top_doc_prob}')
#     return top_prob, word_top_prob, doc_top_prob

probabilistic_latent_semantic_analysis(data=X, topic_num=4)

===============生成模型结果===============
variation: 1.818181818181818, iteration_num:1
variation: 0.0, iteration_num:2
variation: 0.0, iteration_num:3
variation: 0.0, iteration_num:4
variation: 0.0, iteration_num:5
variation: 0.0, iteration_num:6
variation: 0.0, iteration_num:7
variation: 0.0, iteration_num:8
variation: 0.0, iteration_num:9
variation: 0.0, iteration_num:10
文本概率为：
[0.11111111 0.11111111 0.11111111 0.11111111 0.11111111 0.11111111
 0.11111111 0.11111111 0.11111111]
已知话题，单词的条件概率矩阵为：
[[0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.3        0.3        0.3        0.3       ]
 [0.03333333 0.03333333 0.03333333 0.03333333]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.1        0.1        0.1        0.1       ]
 [0.1        0.1        0.1        0.1       ]
 [0.06666667 0.06666667 0.06666667 0.06666667]]
已知文本，话题的条件概率矩阵为：
[[0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25]
 [0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25]
 [0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25]
 [0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25]]

可以发现，而且EM迭代中，收敛很快，只需要一步就收敛了，而最终的结果当中发现都是等概率的，怀疑是收敛到了局部最优，因此调整初值试一下。

def probabilistic_latent_semantic_analysis(data, topic_num=4, max_iter=11):
    word_num, document_num = X.shape
#     topic_num = 3
    # 初始化参数值
#     word_top_prob = np.ones((word_num, topic_num)) / word_num
#     top_doc_prob = np.ones((topic_num, document_num)) / topic_num
    np.random.seed(229)
    word_top_prob = np.random.rand(word_num, topic_num)
    top_doc_prob = np.random.rand(topic_num, document_num)
    doc_prob = np.ones(document_num) / document_num
    # 迭代：
    it = 1
    print('===============生成模型结果===============')
    while it < max_iter:
        # E-step
        top_given_word_doc_prob = np.zeros((topic_num, word_num, document_num))
        for i in range(word_num):
            for j in range(document_num):
                top_given_word_doc_prob[:, i, j] = word_top_prob[i] * top_doc_prob[:, j] / (word_top_prob[i] @ top_doc_prob[:, j])
        # M-step
        old_word_top_prob = word_top_prob.copy()
        for i in range(word_num):
            for k in range(topic_num):
                word_top_prob[i, k] = X[i] @ top_given_word_doc_prob[k, i]
        word_top_prob = word_top_prob / word_top_prob.sum(axis=0)
        for k in range(topic_num):
            for j in range(document_num):
                top_doc_prob[k, j] = X[:, j] @ top_given_word_doc_prob[k, :, j]
        top_doc_prob = top_doc_prob / X.sum(axis=0)
        # 打印看是否有收敛趋势
        if it % 5 == 0:
            delta = np.abs(word_top_prob - old_word_top_prob).sum()
            print(f'variation: {
      
      delta}, iteration_num{
      
      it}')
        it += 1
    print(f'文本概率为：\n{
      
      doc_prob}')
    print(f'已知话题，单词的条件概率矩阵为：\n{
      
      word_top_prob}')
    print(f'已知文本，话题的条件概率矩阵为：\n{
      
      top_doc_prob}')
#     return doc_prob, word_top_prob, top_doc_prob

probabilistic_latent_semantic_analysis(data=X, topic_num=4, max_iter=101)

===============生成模型结果===============
variation: 0.5114324091327377, iteration_num5
variation: 0.11662166821108907, iteration_num10
variation: 0.12379206437008639, iteration_num15
variation: 0.04278888370636651, iteration_num20
variation: 0.043632421409570646, iteration_num25
variation: 0.06534696503586224, iteration_num30
variation: 0.02095661936571032, iteration_num35
variation: 0.004828797428707871, iteration_num40
variation: 0.0010485101291847223, iteration_num45
variation: 0.00021845693893074626, iteration_num50
variation: 4.498000226386677e-05, iteration_num55
variation: 9.235569215255162e-06, iteration_num60
variation: 1.895144030932414e-06, iteration_num65
variation: 3.888337379652317e-07, iteration_num70
variation: 7.977627497089524e-08, iteration_num75
variation: 1.6367452974660436e-08, iteration_num80
variation: 3.358056104353687e-09, iteration_num85
variation: 6.889609560325698e-10, iteration_num90
variation: 1.4135189267652198e-10, iteration_num95
variation: 2.9000758077938096e-11, iteration_num100
文本概率为：
[0.11111111 0.11111111 0.11111111 0.11111111 0.11111111 0.11111111
 0.11111111 0.11111111 0.11111111]
已知话题，单词的条件概率矩阵为：
[[0.00000000e+00 0.00000000e+00 7.55908998e-51 3.04714590e-01]
 [2.47714899e-11 2.71593368e-01 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 0.00000000e+00 1.91635475e-01 0.00000000e+00]
 [3.54858459e-01 1.06475051e-58 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 1.35796684e-01 9.58177377e-02 0.00000000e+00]
 [2.90283081e-01 1.85219895e-01 3.29275836e-01 3.90570819e-01]
 [0.00000000e+00 0.00000000e+00 9.58177377e-02 0.00000000e+00]
 [3.54858459e-01 2.71937977e-58 0.00000000e+00 0.00000000e+00]
 [2.80398767e-24 4.07390053e-01 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 0.00000000e+00 2.87453213e-01 8.32450493e-28]
 [0.00000000e+00 0.00000000e+00 0.00000000e+00 3.04714590e-01]]
已知文本，话题的条件概率矩阵为：
[[1.87158297e-61 9.18458873e-38 4.17502748e-57 2.43283173e-62
  8.86381972e-45 3.59393193e-45 1.00000000e+00 3.33588575e-51
  5.27209989e-01]
 [8.57113811e-23 5.24311756e-56 2.77411267e-74 7.09035687e-79
  9.47233048e-63 1.00000000e+00 3.66748170e-64 3.19998005e-69
  4.72790011e-01]
 [1.00000000e+00 1.00000000e+00 4.78827003e-01 4.41128160e-60
  4.14776208e-51 1.50886408e-39 8.58818855e-55 1.00000000e+00
  1.14076662e-66]
 [3.68046765e-47 1.23151761e-20 5.21172997e-01 1.00000000e+00
  1.00000000e+00 8.46753425e-38 8.62987531e-34 3.93193106e-36
  3.80850613e-48]]

可以发现现在的结果比较可靠了，其中文本概率矩阵直接统计得到，因此含义比较明了，没有进一步说明的必要了，对于单词-话题概率矩阵，为了清晰，给出下图：

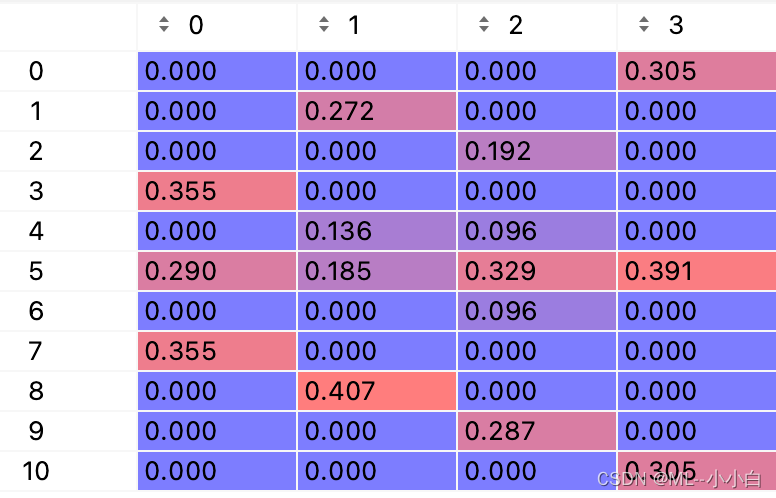
可以发现，第一个话题代表单词为，estate、real、investing，这个可以搜一下，由本书叫《Real Estate Investing from A to Z》，讲的是房地产投资，因此这个话题应该是房地产投资；第二个话题的代表单词为，rich、dads、investing、guide，搜一下有本书叫《Rich Dad’s Guide To Investing (Kiyosaki, Lechter)》，应该是本投资理财的个人科普大众书，估计该话题谈这本书，或者大众个人投资指导；第三个话题代表单词为，investing、stock、dummies、market、guide，搜一下有本书叫《傻瓜个人投资及商业系列（Stock.Investing.For.Dummies）》，主要是讲股票投资的入门，因此该话题要么是关于这本书，要么是股票投资；第四个话题，代表单词为，investing、book、value，搜一下有本书叫《The Little Book of Value Investing》，价值投资建议，至此，估计这些数据可能来自书评，分别评论了不同的书籍。
再看一下，话题-文本概率矩阵：

可以发现第7个文本在谈论第一个话题，第6个文本在谈论第二个话题，第9个文本在应该提及或者说比较了第一、二话题中的两本书，第1、2、8个文本都在讨论第三本书的话题，第4、5文本在谈论第四个话题的书，第3个文本在比较第三和第四话题的书。

# 共现模型的EM算法
def probabilistic_latent_semantic_analysis2(data, topic_num=4, max_iter=11):
    word_num, document_num = X.shape
#     topic_num = 3
    # 初始化参数值
    top_prob = np.ones(topic_num) / topic_num
    word_top_prob = np.ones((word_num, topic_num)) / word_num
    doc_top_prob = np.ones((document_num, topic_num)) / document_num
#     np.random.seed(229)
#     top_prob = np.random.rand(topic_num)
#     word_top_prob = np.random.rand(word_num, topic_num)
#     doc_top_prob = np.random.rand(document_num, topic_num)
    # 迭代：
    it = 1
    print('===============共现模型结果===============')
    while it < max_iter:
        # E-step
        top_given_word_doc_prob = np.zeros((topic_num, word_num, document_num))
        for i in range(word_num):
            for j in range(document_num):
                top_given_word_doc_prob[:, i, j] = word_top_prob[i] * doc_top_prob[j] / (word_top_prob[i] * doc_top_prob[j] * top_prob).sum()
        # M-step
        old_word_top_prob = word_top_prob.copy()
        for i in range(word_num):
            for k in range(topic_num):
                word_top_prob[i, k] = X[i] @ top_given_word_doc_prob[k, i]
        word_top_prob = word_top_prob / word_top_prob.sum(axis=0)
        for j in range(document_num):
            for k in range(topic_num):
                doc_top_prob[j, k] = X[:, j] @ top_given_word_doc_prob[k, :, j]
        doc_top_prob = doc_top_prob / doc_top_prob.sum(axis=0)
        # 打印看是否有收敛趋势
        if it % 1 == 0:
            delta = np.abs(word_top_prob - old_word_top_prob).sum()
            print(f'variation: {
      
      delta}, iteration_num{
      
      it}')
        it += 1
    print(f'话题概率为：\n{
      
      top_prob}')
    print(f'已知话题，单词的条件概率矩阵为：\n{
      
      word_top_prob}')
    print(f'已知话题，文本的条件概率矩阵为：\n{
      
      doc_top_prob}')
#     return doc_prob, word_top_prob, top_doc_prob

probabilistic_latent_semantic_analysis2(data=X, topic_num=4, max_iter=11)

===============共现模型结果===============
variation: 1.818181818181818, iteration_num1
variation: 0.0, iteration_num2
variation: 0.0, iteration_num3
variation: 0.0, iteration_num4
variation: 0.0, iteration_num5
variation: 0.0, iteration_num6
variation: 0.0, iteration_num7
variation: 0.0, iteration_num8
variation: 0.0, iteration_num9
variation: 0.0, iteration_num10
话题概率为：
[0.25 0.25 0.25 0.25]
已知话题，单词的条件概率矩阵为：
[[0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.3        0.3        0.3        0.3       ]
 [0.03333333 0.03333333 0.03333333 0.03333333]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.1        0.1        0.1        0.1       ]
 [0.1        0.1        0.1        0.1       ]
 [0.06666667 0.06666667 0.06666667 0.06666667]]
已知话题，文本的条件概率矩阵为：
[[0.13333333 0.13333333 0.13333333 0.13333333]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.1        0.1        0.1        0.1       ]
 [0.1        0.1        0.1        0.1       ]
 [0.06666667 0.06666667 0.06666667 0.06666667]
 [0.16666667 0.16666667 0.16666667 0.16666667]
 [0.1        0.1        0.1        0.1       ]
 [0.1        0.1        0.1        0.1       ]
 [0.16666667 0.16666667 0.16666667 0.16666667]]

和生成模型结果同样，可以发现，而且EM迭代中，收敛很快，只需要一步就收敛了，而最终的结果当中发现都是等概率的，怀疑是收敛到了局部最优，因此调整初值试一下。

# 共现模型的EM算法
def probabilistic_latent_semantic_analysis2(data, topic_num=4, max_iter=11):
    word_num, document_num = X.shape
#     topic_num = 3
    # 初始化参数值
#     top_prob = np.ones(topic_num) / topic_num
#     word_top_prob = np.ones((word_num, topic_num)) / word_num
#     doc_top_prob = np.ones((document_num, topic_num)) / document_num
    np.random.seed(229)
    top_prob = np.random.rand(topic_num)
    word_top_prob = np.random.rand(word_num, topic_num)
    doc_top_prob = np.random.rand(document_num, topic_num)
    # 迭代：
    it = 1
    print('===============共现模型结果===============')
    while it < max_iter:
        # E-step
        top_given_word_doc_prob = np.zeros((topic_num, word_num, document_num))
        for i in range(word_num):
            for j in range(document_num):
                top_given_word_doc_prob[:, i, j] = word_top_prob[i] * doc_top_prob[j] / (word_top_prob[i] * doc_top_prob[j] * top_prob).sum()
        # M-step
        old_word_top_prob = word_top_prob.copy()
        for i in range(word_num):
            for k in range(topic_num):
                word_top_prob[i, k] = X[i] @ top_given_word_doc_prob[k, i]
        word_top_prob = word_top_prob / word_top_prob.sum(axis=0)
        for j in range(document_num):
            for k in range(topic_num):
                doc_top_prob[j, k] = X[:, j] @ top_given_word_doc_prob[k, :, j]
        doc_top_prob = doc_top_prob / doc_top_prob.sum(axis=0)
        # 打印看是否有收敛趋势
        if it % 5 == 0:
            delta = np.abs(word_top_prob - old_word_top_prob).sum()
            print(f'variation: {
      
      delta}, iteration_num{
      
      it}')
        it += 1
    print(f'话题概率为：\n{
      
      top_prob}')
    print(f'已知话题，单词的条件概率矩阵为：\n{
      
      word_top_prob}')
    print(f'已知话题，文本的条件概率矩阵为：\n{
      
      doc_top_prob}')
#     return doc_prob, word_top_prob, top_doc_prob

probabilistic_latent_semantic_analysis2(data=X, topic_num=4, max_iter=101)

===============共现模型结果===============
variation: 0.2551141724037168, iteration_num5
variation: 0.13996994807037552, iteration_num10
variation: 0.09237080708286682, iteration_num15
variation: 0.04610298691056777, iteration_num20
variation: 0.013475887500524024, iteration_num25
variation: 0.00619301007033629, iteration_num30
variation: 0.003468361110527294, iteration_num35
variation: 0.0021556648912154355, iteration_num40
variation: 0.0014247779735354815, iteration_num45
variation: 0.000982627032814392, iteration_num50
variation: 0.0007031864894675868, iteration_num55
variation: 0.0005106018787468878, iteration_num60
variation: 0.00037358500286936014, iteration_num65
variation: 0.0002734519445434847, iteration_num70
variation: 0.00020248692085259195, iteration_num75
variation: 0.0001609478428811367, iteration_num80
variation: 0.00012927367905240847, iteration_num85
variation: 0.00010677530922985633, iteration_num90
variation: 9.763081822485289e-05, iteration_num95
variation: 0.00010320088730115618, iteration_num100
话题概率为：
[0.097025   0.73855721 0.67878381 0.24754234]
已知话题，单词的条件概率矩阵为：
[[0.00000000e+000 0.00000000e+000 2.05413039e-001 3.59137766e-049]
 [0.00000000e+000 1.99999998e-001 0.00000000e+000 0.00000000e+000]
 [0.00000000e+000 0.00000000e+000 1.33853335e-189 3.04611828e-001]
 [0.00000000e+000 1.00000002e-001 1.02706516e-001 0.00000000e+000]
 [2.70432059e-001 9.99999993e-002 1.98625997e-263 3.51037107e-103]
 [2.25327352e-001 2.00000000e-001 3.83760889e-001 3.70150165e-001]
 [2.70432059e-001 0.00000000e+000 7.45201925e-262 4.35714054e-103]
 [0.00000000e+000 1.00000002e-001 1.02706516e-001 0.00000000e+000]
 [0.00000000e+000 2.99999998e-001 0.00000000e+000 0.00000000e+000]
 [2.33808530e-001 0.00000000e+000 3.44108778e-017 3.25238007e-001]
 [0.00000000e+000 0.00000000e+000 2.05413039e-001 0.00000000e+000]]
已知话题，文本的条件概率矩阵为：
[[1.00000000e+000 2.06980753e-010 1.30583309e-003 4.40924626e-002]
 [2.07488328e-060 3.84101633e-026 3.33570095e-004 3.04117169e-001]
 [3.92652212e-039 4.42878481e-061 1.76708449e-001 1.94872626e-001]
 [1.92457585e-111 1.61842504e-072 3.08119558e-001 1.15024119e-074]
 [1.07837295e-094 9.64963367e-057 2.05413039e-001 2.83460821e-062]
 [2.67238430e-054 4.99999996e-001 8.12994714e-047 4.41904793e-076]
 [8.63825967e-113 7.85623776e-009 3.08119550e-001 1.77935745e-079]
 [5.66207893e-051 2.62510381e-043 7.03969243e-019 4.56917742e-001]
 [1.11956533e-110 4.99999996e-001 3.85203336e-013 3.70503931e-078]]

该结果中单词-话题矩阵与生成模型稍有不同，猜测可能是不同的方法所致，其他的粉丝思路类似，不再赘述。