【海量数据挖掘/数据分析】之贝叶斯分类算法（朴素贝叶斯分类、贝叶斯分类计算流程、拉普拉斯修正、贝叶斯分类实例计算）

一、贝叶斯分类器

1 . 贝叶斯分类器 :

2 . 贝叶斯分类器的类型 :

3 . 正向概率与逆向概率 :

4 . 贝叶斯公式 : 有两个事件 , 事件 A , 和事件 B ;

一、贝叶斯分类器

1 . 贝叶斯分类器 :

① 原理 : 基于统计学方法贝叶斯 ( Bayes ) 理论 , 预测样本某个属性的分类概率 ;

② 性能分析 : 朴素贝叶斯分类器 , 与决策树 , 神经网络分类器性能基本相同 , 性能指标处于同一数量级 , 适合大数据处理 ;

2 . 贝叶斯分类器的类型 :

① 朴素贝叶斯分类器 : 样本属性都是独立的 ;

② 贝叶斯信念网络 : 样本属性间有依赖关系的情况 ;

3 . 正向概率与逆向概率 :

① 正向概率 : 盒子中有 N 个白球 , M 个黑球 , 摸出黑球的概率是 M /N + M ;

② 逆向概率 : 事先不知道盒子中白球和黑球的数量 , 任意摸出X 个球 , 通过观察这些球的颜色 , 推测盒子中有多少白球 , 多少黑球 ;

4 . 贝叶斯公式 : 有两个事件 , 事件 A , 和事件 B ;

公式：

简写形式：

或者：

① 事件 A A A 发生的概率 : 表示为 P(A) ;

② 事件 B B B 发生的概率 : 表示为 P(B) ;

③ A B 两个事件同时发生的概率 : 表示为 P(A,B) ;

④ 事件 A 发生时 B 发生的概率 : 表示为 P(B∣A) ;

⑤ 事件 B 发生时 A 发生的概率 : 表示为 P(A∣B) ;

二、贝叶斯分类器处理多属性数据集方案

1 . 多属性特征 : 如果要处理的样本数据的特征有 n 个属性 , 其取值{X1,X2,⋯,Xn} 组成了向量 X ;

2 . 后验概率 : 计算最终分类为 C1 时 , 多个属性的取值为 X 向量的概率 , 即 P(X∣C1)

3 . 朴素贝叶斯由来 : 朴素地认为这些属性之间不存在依赖关系 , 就可以使用乘法法则计算这些属性取值同时发生的概率 ;

4 . 计算单个分类概率 : 分类为 C1 时 n 个属性每个取值取值概率 :

1）当最终分类为 C1 时 , 第 1 个属性取值 X1 的概率为 P(X1∣C1) ;

2）当最终分类为 C1 时 , 第 2 个属性取值 X2 的概率为 P(X2∣C1) ;

3）当最终分类为 C1 时 , 第 n 个属性取值 Xn 的概率为 P(Xn∣C1) ;

4）最终分类为 C1 时 , n 个属性取值 X 向量的概率为 :

5 . 多属性分类概率总结 : 分类为 Ci 时 n 个属性取值 X 向量的概率为 :

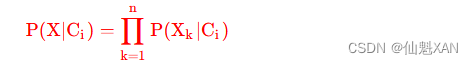
6 . 上述公式中的分类属性 P(Xk∣Ci) 计算方式 : 如果第 k 个属性的取值是离散的 , 即分类属性 , 那么通过以下公式计算 :

Si 是分类为 Ci 类型的数据集样本个数 ;

Sik 是被分类成 Ci 类型的样本中 , 并且第 k 个值是 Xk 的样本个数 ;

7 . 样本分类 :

① 样本 : 给出未知属性类型样本 , 其 n 个已知的属性取值为 X 向量 ;

② 分类个数 : 其根据分类属性可能分为 m 类 ;

③ 分类 : 求其取值为 X 向量时 , 分类为 Ci 的概率 , 哪个概率最大 , 其被分为哪个 Ci 类型 , 表示为

④ 后验概率 : 多属性取值为 X 向量时 , 分类为 Ci 的概率进行比较 , 分母都是 P(X) , 是一个常数 , 可以不考虑这种情况 , 只比较 P(Ci) 值的大小 , P(X∣Ci)P(Ci) 值最大的情况 , 就是分类的目标分类 Ci , 也就是后验概率 ;

三、贝叶斯分类器分类的流程

已知条件 :

已知样本 : 已知若干个样本

未知样本 : 给定 1 个未知样本 , 其有 4 个属性组成向量 X , 样本的分类有两种 , Y 和 N ; ( Yes / No )

分类步骤 :

计算两个概率 , 即

① 样本取值为 X 向量时 , 分类为 Y 的概率 , 公式为 P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y )/ P ( X ) , 其中 P ( X ∣ Y ) P ( Y ) 含义是 : 样本分类 Y 的概率 P(Y) , 乘以样本分类为 YY 前提下样本取值 X X 时的概率 P ( P(X∣Y) , 是 P(XY) 共同发生的概率 ;

② 样本取值为 X 向量时 , 分类为 N 的概率 , 公式为 P(N∣X)=P(X)P(X∣N)/P(N) , 其中 P ( X ∣ N ) P ( N )含义是 : 样本分类为 N 的概率 P(N) , 乘以样本取值 N 时的概率 P(X∣N) , 是 P(XN) 共同发生的概率 ;

上述两个概率 , 哪个概率高 , 就将该样本分为哪个分类 ;

先验概率 : P ( Y ) , P ( N ) ;

后验概率 : P ( X ∣ Y ) P ( Y ) , P ( X ∣ N ) P ( N ) ;

上述两个公式 P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y ) / P ( X ) 和 P ( N ∣ X ) = P ( X ∣ N ) P ( N )/ P ( X ) , 分母都是 P ( X ) , 只比较分子即可; 其中先验概率 P ( Y ) , P ( N ) 很容易求得 , 重点是求两个后验概率 P ( X ∣ Y ) P ( Y ) , P ( X ∣ N ) P ( N ) ;

后验概率 P ( X ∣ Y ) 求法 : 针对 X 向量中 4 个分量属性的取值 , 当样品类型是 Y 时 , 分量 1 取值为该分量属性时的概率 , 同理计算出 4 个分量属性对应的 4 个概率 , 最后将四个概率相乘 ;

后验概率 P ( X ∣ Y ) 再乘以先验概率 P ( Y ) , 就是最终的 未知样本分类为 Y 类型的概率 ;

最终对比样本 , ① 未知样本分类为 Y 类型的概率 , ② 未知样本分类为 N 类型的概率 , 哪个概率大 , 就分类为哪个类型 ;

四、拉普拉斯修正

在计算后验概率 P ( X ∣ Y ) 时 , 需要计算出当样品类型是 Y 时 , X 向量的分量 1 取值为该分量属性时的概率 , 同理计算出 4 个分量属性对应的 4 个概率 , 最后将四个概率相乘 ;

如果上述 4 个相乘的概率其中有一个是 0 , 那么最终结果肯定就是 0 , 这里需要避免这种情况 , 引入拉普拉斯修正 ;

拉普拉斯修正 :

① 计算先验概率时进行拉普拉斯修正 :

Dc 表示训练集中 , 分类为 C 的样本个数 ;
D 表示训练集中样本中个数 ;
N 表示按照某属性分类的类别数 , 如 , 是否购买商品 , 是或否两种可取值类别 , 这里 N=2 ;

② 计算类条件概率 ( 似然 ) 时进行拉普拉斯修正 :

Si 是分类为 Ci 类型的数据集样本个数 ;
Sik 是被分类成 Ci 类型的样本中 , 并且第 k 个值是 Xk 的样本个数 ;
Ni 表示该属性的可取值个数 , 如 , 是否购买商品 , 是或否两种可取值类别 , 这里 Ni=2 ;

举例子说明 ;

如果计算时 , 9 个样本是购买商品的 , 但年龄都大于 30 , 计算过程如下 ;

P(年龄小于30∣Y)=0/9

拉普拉斯修正就是分子加 1 , 分母加上样本类型个数 2 ; ( 样本有两个类型 , Y 购买商品 , N 不购买商品 ) ;

P(年龄小于30∣Y)=0+1 / 9+2=1 / 11

注意是所有的分量的概率都要进行拉普拉斯修正 , 不能只修正这一个 ;

五、贝叶斯分类器示例

分类需求 : 根据年龄 , 收入水平 , 级别 , 部门 , 人数 , 预测 " 年龄 31..35, 收入 41 k . . 41k..45k , systems 部门 " 的员工级别 ;

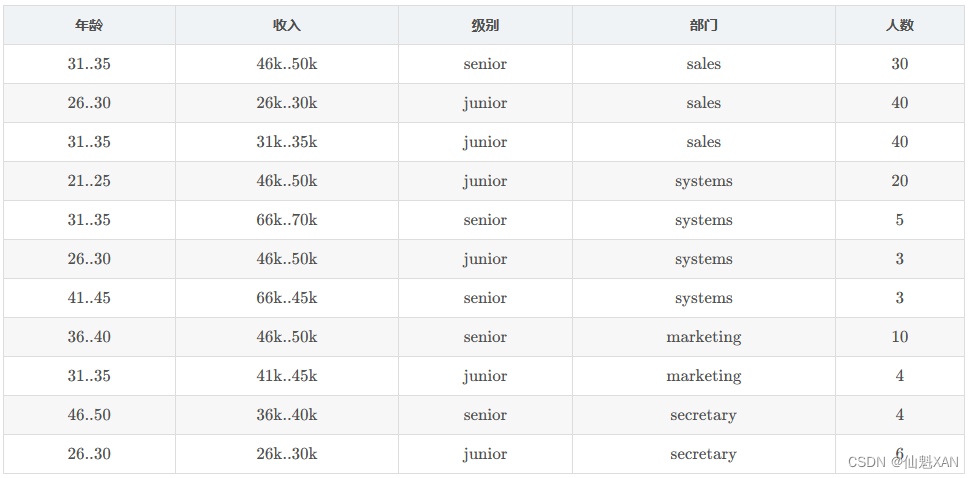
未知样本取值 X 向量 为 " 年龄 31..35, 收入 41k..45k , systems 部门 " ;

未知样本分类为 senior ( 高级 ) 类型的概率 : P(senior∣X)=P(X∣senior)P(senior)/P(X)

未知样本分类为 junior ( 低级 ) 类型的概率 : P(junior∣X)=P(X∣junior)P(junior)/P(X)

上述两个概率的分母 P(X) 是常数 , 对比时可以忽略 , 只需要对比分子即可 ;

先验概率 P ( s e n i o r ) = 52 / 165 , P ( j u n i o r ) = 113 / 165 , 52 个人是 senior 级别 , 113 个人是 junior 级别 ;

后验概率

① P ( X ∣ s e n i o r ) = P ( 年龄 31..35 ∣ s e n i o r ) × P ( 收入 41 k . . 45 k ∣ s e n i o r ) × P ( 部门 s y s t e m s ∣ s e n i o r ) = 8 / 52 × 35/ 52 × 0 /52

上述后验概率的结果为 0 , 需要进行拉普拉斯修正 , 上述式子中的三个概率分子都需要 +1 , 分母分母是分类的个数 , senior 和 junior 两个分类下各自包含的该属性分类的类别数 , 因此分母对应增加：年龄为 +4，收入为 +4，部门为 +4 ;

拉普拉斯修正后的结果 :

P ( X ∣ s e n i o r ) = （(8 + 1) / (52 + 4) ）× ((35 + 1 )/ (52 + 4)) × ((0 + 1) / (52 + 2)) = (9 / 56 )× (36./ 56) × (1/ 56 )

② P ( X ∣ j u n i o r ) = P ( 年龄 31..35 ∣ j u n i o r ) × P ( 收入 41 k . . 45 k ∣ j u n i o r ) × P ( 部门 s y s t e m s ∣ j u n i o r ) = 23 ./ 113 × 44 /113 × 4 /113

1）未知样本 分类为 Y 类型的概率分子 : P ( X ∣ s e n i o r ) P ( s e n i o r ) =(9 / 56 )× (36./ 56) × (1/ 56 ) = 0.00058

2）未知样本 分类为 N 类型的概率分子 : P ( X ∣ j u n i o r ) P ( j u n i o r ) = 23 113 × 44 113 × 4 113 × 113 165 ≈ 0.0024

该样本分类为 junior , 是低级员工 ;

六、朴素贝叶斯分类器使用

1 . 要求分类速度快 : 此时先计算出所有数据的概率估值 , 分类时 , 直接查表计算 ;

2 . 数据集频繁变化 : 使用懒惰学习的策略 , 收到分类请求时 , 再进行训练 , 然后预测 , 分类速度肯定变慢 , 但是预测准确 ;

3 . 数据不断增加 : 使用增量学习策略 , 原来的估值不变 , 对新样本进行训练 , 然后基于新样本的估值修正原来的估值 ;

七、朴素贝叶斯分类的优缺点

朴素贝叶斯分类 :

优点 : 只用几个公式实现 , 代码简单 , 结果大多数情况下比较准确
缺点 : 假设的属性独立实际上不存在 , 属性间是存在关联的 , 这会导致部分分类结果不准确

针对属性间存在依赖的情况 , 使用 贝叶斯信念网络 方法进行分类 ;

参考内容：

【数据挖掘】数据挖掘总结 ( 贝叶斯分类器 ) ★_贝叶斯分类器实验

【数据挖掘】数据挖掘总结 ( 贝叶斯分类器示例 ) ★_数据挖掘贝叶斯分类例题

【数据挖掘】数据挖掘总结 ( 拉普拉斯修正 | 贝叶斯分类器示例2 ) ★_拉普拉斯修正例题