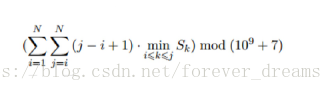【题目】
题目描述:
给定一个长度为 N 的正整数序列 S,求下列式子的值:
输入格式:
第一行 1 个正整数 N 表示 S 的长度
接下来一行 N 个正整数 Si
输出格式:
输出一行表示答案
样例数据:
输入
5
1 2 3 4 5输出
70
备注:
数据规模与约定:
20% 数据,N ≤ 200
50% 数据,N ≤ 1000
100% 数据,1 ≤ N ≤ 100000,1 ≤ Si ≤
【分析】
emmm其实暴力稍加优化能过60分
题目的意思就是枚举所有的区间,然后将区间的最小值乘区间长度加进答案,最后取模
100分的思路:
枚举所有的点,找出以每个点的值作为最小值能到的最左边的点和最右边的点
假设现在枚举到了点 x,最左边的点为 l,最右边的点为 r,那么在区间 [ l , r ] 中,最小的点就是 x,它的值为 s[ x ]
定义 L 为区间 [ l , x ] 的长度,R 为区间 [ x , r ] 的长度
我们从 [ x , r ] 中枚举每一个右端点,然后在这个右端点的基础上枚举左端点(在 [ l , x ] 中),统计答案
(那个,大家应该都会等差数列吧,不会的我也救不了你,自行百度吧)
当右端点为 x 时,答案:s[ x ] *(1 + 2 + …… + L)= s[ x ] * L *(L + 1)/ 2
当右端点为(x + 1)时,答案:s[ x ] *(2 + 3 + …… + L + 1)= s[ x ] * L *(L + 3)/ 2
当右端点为(x + 2)时,答案:s[ x ] *(3 + 4 + …… + L + 2)= s[ x ] * L *(L + 5)/ 2
……
当右端点为 r(即 x + R - 1)时,答案:s[ x ] *(R + R + 1 + …… + L + R - 1)= s[ x ] * L *(L + 2 * R - 1)/ 2
这样把所有答案加起来后再化简得到 s[ x ] *(L + R)* L * R / 2
也就是说只要我们知道以一个点为最小值能到的最远的两个点,就能在O(1)的复杂度内统计当前的答案
而这个最远的两个点我们就用单调栈来找,复杂度为O(n)
单调栈的话我就不赘述了,大家可以找百度了解一下
【代码】
#include<cstdio>
#include<cstring>
using namespace std;
const int N=100005;
const int mod=1e9+7;
int s[N],l[N],r[N],id[N],sta[N];
int main()
{
// freopen("sequence.in","r",stdin);
// freopen("sequence.out","w",stdout);
int n,i,top;
long long L,R,ans=0;
scanf("%d",&n);
for(i=1;i<=n;++i)
scanf("%d",&s[i]);
top=0,i=1; //用单调栈找以i为最小值的最左边的点
while(i<=n)
{
while(top&&sta[top]>s[i]) top--;
l[i]=id[top]+1;
sta[++top]=s[i];
id[top]=i;
i++;
}
top=0,i=n,id[0]=n+1; //用单调栈找以i为最小值的最右边的点
while(i>=1)
{
while(top&&sta[top]>s[i]) top--;
r[i]=id[top]-1;
sta[++top]=s[i];
id[top]=i;
i--;
}
for(i=1;i<=n;++i)
{
L=i-l[i]+1; //L,R分别是左边部分和右边部分的长度
R=r[i]-i+1;
ans=(ans+s[i]*(L+R)*L*R/2)%mod; //用推出来的公式计算答案
}
printf("%lld",ans);
// fclose(stdin);
// fclose(stdout);
return 0;
}