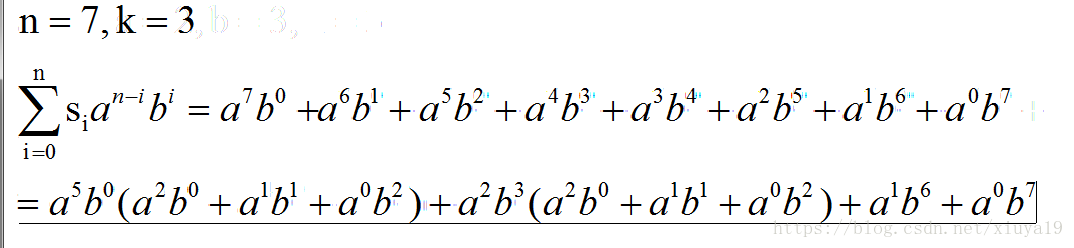A. Splits
给出一个数字n,把它分裂成多个数相加,对于分裂得到的序列,其权重设为序列中第一个数字有多少个。
问n能分成多少种不同权重的序列。
比赛时大胆猜结论结果为 n/2+1
现在分析一下,首先要分出多个相同数字,设k为权重,那么第一个数字就是n/k(k=1,2,3...)(这里的除法是算术除法)
所以只要知道k有多少就行了。
由于是算术除法,当k>=n/2时,n/k=1。
k最大只能到n/2再加上全为1的一项。
即n/2+1
#include<iostream>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<algorithm>
#include<queue>
#include<set>
#include<cstdio>
#include<functional>
#include<iomanip>
#include<cmath>
#include<stack>
#include<iomanip>
#include<functional>
using namespace std;
const int maxn = (int)(1e5) + 10;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const double eps = 1e-6;
typedef long long LL;
typedef unsigned long long ull;
int main() {
int n;
while (~scanf("%d", &n)) {
printf("%d\n", n / 2 + 1);
}
return 0;
}B. Messages
Vasya在收邮件,现在给出每封邮件的收到时间,并且每封邮件的价值都为A
如果Vasya收到邮件不读的话,其价值会每分钟减少B
但是每分钟Vasya会收到C*(Vasya所持有的未读的邮件数)
任何时候Vasya都可以读未读的邮件,读了未读的邮件Vasya会收到该邮件的价值
当第T分钟时Vasya会把未读的邮件都读。
问Vasya能收到最大的价值是多少。
对于某一封邮件,如果不读,其价值会减少B,但是会收到C的价值
这相当于这封信的价值每分钟增加C-B
如果C-B>0的话,不读的话邮件会不断升值,即最后一次全读有最大价值。
如果C-B<0的话,不读的话邮件会不断贬值,即收到就读有最大价值。
(笔者比赛时手滑把n写成t就结果过了pre,最后测试wa的难受到爆炸)
#include<iostream>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<algorithm>
#include<queue>
#include<set>
#include<cstdio>
#include<functional>
#include<iomanip>
#include<cmath>
#include<stack>
#include<iomanip>
#include<functional>
using namespace std;
const int maxn = (int)(1e5) + 10;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 7;
const double eps = 1e-6;
typedef long long LL;
typedef unsigned long long ull;
int val[1111];
int main() {
int a, b, c, n, t;
while (~scanf("%d%d%d%d%d", &n, &a, &b, &c, &t)) {
for (int i = 0; i < n; i++)
scanf("%d", &val[i]);
if (b >= c)
printf("%d\n", n*a);
else {
int ans = 0;
for (int i = 0; i <n; i++)
ans += (c - b)*(t - val[i]);
printf("%d\n", ans + n*a);
}
}
return 0;
}C. Alternating Sum
给出公式,求和(符号不够时循环使用)
因为n太大了不能直接一个一个算,然后看到k<=1e5。
就想到是不是按k分组有规律
如果对其每k个分组,然后对组内成员提取公共因子,能等到被提取的k个元素都是相同的
举例如下
可知只要算出公共项就能减少计算量,
时间复杂度下降为O(n/k+k+(余项个数)) ,
显然当k很小的时候这样还是会爆炸,优化吧。
因为k<=1e5 所以当n<k时计算量不会超过1e5,
当n>>k时(远远大于),明显计算量有可能超1e7~1e8。
但是这时,因为k是被循环使用的,这样的话我们可以使k变长(就是把分组间距加大),
这样就可以把计算量压缩了。
还有一点要注意的是,上述过程还没加入符号位的计算,
所以尽量多修正吧。
#include<iostream>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<algorithm>
#include<queue>
#include<set>
#include<cstdio>
#include<functional>
#include<iomanip>
#include<cmath>
#include<stack>
#include<iomanip>
#include<functional>
using namespace std;
const int maxn = (int)(1e5) + 10;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 9;
const double eps = 1e-6;
typedef long long LL;
typedef unsigned long long ull;
char op[maxn];
LL quick_mod(LL a, LL b) {
LL ans = 1;
a = a % mod;
while (b) {
if (b & 1)ans = (ans * a) % mod;
b >>= 1;
a = (a * a) % mod;
}
return ans%mod;
}
int main() {
LL n, a, b, k;
while (~scanf("%I64d%I64d%I64d%I64d", &n, &a, &b, &k)) {
scanf("%s", op);
while (k*k < n) {//压缩数据
for (int i = 0; i < k; i++)
op[i + k] = op[i];
k = 2 * k;
}
LL tmp = 0;
for (LL i = k - 1, j = 0; j < k; i--, j++) {//因为不知道tmp的正负所以通通修正
if (op[j] == '+')
tmp = ((tmp + quick_mod(a, i)*quick_mod(b, j) % mod) % mod + mod) % mod;
else
tmp = ((tmp - quick_mod(a, i)*quick_mod(b, j) % mod) % mod + mod) % mod;
}
LL ans = 0;
LL st = n + 1 - k, ed = 0;//提取项a的指数和b的指数
for (int i = 0; i < (n + 1) / k; i++) {
ans = ((ans + quick_mod(a, st)*quick_mod(b, ed)%mod*tmp%mod) % mod + mod) % mod;
st -= k, ed += k;
}
st = n - (n + 1) / k*k, ed = n - st;//余项的a的指数和b的指数
for (int i = 0; i < n + 1 - ((n + 1) / k)*k; i++) {
if (op[i] == '+')
ans = ((ans + quick_mod(a, st)*quick_mod(b, ed)) % mod + mod) % mod;
else
ans = ((ans - quick_mod(a, st)*quick_mod(b, ed)) % mod + mod) % mod;
st--, ed++;
}
printf("%I64d\n", ans);
}
return 0;
}D. Destruction of a Tree
给出一棵树,你每次能剔除度数为偶数的点,问能不能把树的所有点都剔除
显然因为n为偶数时,边树为n-1
剔除度数为偶数的点相当于减去偶数条边,然而节点数位n的树边为奇数条所以一定 不能全剔除
反之n为奇数时则一定能
对这棵树下向上把只有奇树子结点的当前结点删掉。
再从上向下,删掉没删的点就行了。
#include<iostream>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<algorithm>
#include<queue>
#include<set>
#include<cstdio>
#include<functional>
#include<iomanip>
#include<cmath>
#include<stack>
#include<iomanip>
#include<functional>
using namespace std;
const int maxn = 2*(int)(1e5) + 10;
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 9;
const double eps = 1e-6;
typedef long long LL;
typedef unsigned long long ull;
vector<int> edge[maxn];
int sz[maxn];
void dfs1(int u) {
sz[u] = 1;
for (int i = 0; i < edge[u].size(); i++) {
int v = edge[u][i];
dfs1(v);
sz[u] += sz[v];
}
}
void dfs2(int u) {
for (int i = 0; i < edge[u].size(); i++) {
int v = edge[u][i];
if (sz[v] % 2 == 0)
dfs2(v);
}
printf("%d\n", u);
for (int i = 0; i < edge[u].size(); i++) {
int v = edge[u][i];
if (sz[v] % 2)
dfs2(v);
}
}
int main() {
int n;
while (~scanf("%d", &n)) {
for (int i = 1; i <= n; i++)
edge[i].clear();
int root, v;
for (int u = 1; u <= n; u++) {
scanf("%d", &v);
if (!v)
root = u;
edge[v].push_back(u);
}
if (n % 2 == 0) {
printf("NO\n");
continue;
}
else {
printf("YES\n");
dfs1(root);
dfs2(root);
}
}
return 0;
}E题不存在的