一、二叉树遍历
已知前序遍历和中序遍历,可以唯一确定一棵二叉树;
已知后序遍历和中序遍历,可以唯一确定一棵二叉树;
已知前序遍历和后序遍历,一般不能唯一确定一课二叉树;
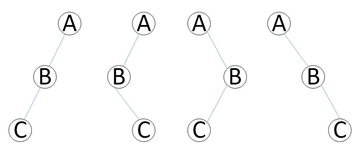
当只知道一棵树的前序遍历和后序遍历时,我们只能确定该树的根节点,
比如前序遍历ABC,后序遍历CBA,二叉树可能的情况为:
常见题目
1.根据前序和后序,判断不会出现的中序
2.已知二叉树的前序遍历和后序遍历,求二叉树中序遍历的可能情况数?
已知前序遍历和后序遍历的情况下,中序遍历的可能性是不确定的,不确定性来源于当某个节点只有一个分支时,不确定该分支是左子树还是右子树造成的。例如前序遍历ab,后序遍历ba,a为根,b为子树,则中序遍历可能是ab,也可能是ba。所以当这种节点有n个时,中序遍历的可能性就有2^n种。

那么问题就转变为求这种节点的数量。可以总结一个规律,前序遍历ab,后序遍历ba,此时无法确定b为左孩子还是右孩子,那么就产生了一个特殊节点。所以规律就是(a,b分别是前序遍历和后序遍历的字符串),a[i]==b[j]且a[i+1]==b[j-1]时产生一个特殊节点。
//已知前序遍历和后序遍历,求中序遍历的可能性有多少种数量?
int InorderNumbers()
{
char s1[30];
char s2[30];
int len1 = 0, len2 = 0, count = 0;
printf("请输入二叉树的前序遍历:\n");
scanf("%s", s1);
printf("请输入二叉树的中序遍历:\n");
scanf("%s", s2);
len1 = strlen(s1);
len2 = strlen(s2);
for (int i = 0; i < len1-1; i++)
{
for (int j = 1; j < len2; j++)
{
if (s1[i] == s2[j] && s1[i + 1] == s2[j - 1])
{
count++;//特殊节点个数
}
}
}
return pow(2,count);
}已知中序后序求前序:
中序序列为A、B、C、D、E、F、G,后序序列为B、D、C、A、F、G、E,求先序:
先看后序,再看前序,后序最后一个为E,所以根节点为E,再看前序,E左边的A,B,C,D为左子树,E右边的F,G为右子树;
再看后序中右子树F,G,G在后面,所以G为E的右孩子,再看中序中F,G,F在G前面,F为G的左孩子;
再看后序中B,D,C,A和前序中A,B,C,D,后序中A最后一个访问,A为E的左孩子。。。
。。。
二、二叉树的性质
1.在二叉树的第i层上至多有2^(i-1)个结点
2.深度为k的二叉树至多有2^k-1个节点
3.二叉树中,如果终端节点数为n0,度为2的节点数为n2,则n0=n2+1
设二叉树中度为0的节点数为n0,度为1的节点数为n1,度为2的节点数为n2,总的节点数为n,则
n=n0+n1+n2;
又树中边数e=n-1,每个2度节点分支数为2,每个1度顶点分支数为1,所以n-1=2n2+n1
所以n0+n1+n2=n1+2n2+1;得到n0=n2+1
4.具有n个节点的完全二叉树的深度为向下取整(log2n)+1。
设二叉树深度k,则2^(k-1)-1<n,又k为整数,有2^(k-1)<=n,即k<=logn +1
又n<=2^k -1,即n<2^k,取对数得,k>logn,综合logn<k<=logn +1
所以k=向下取整(log2n) +1 。
5.对于一棵完全二叉树,按层序编号时,对于任意节点i(i从0开始编号),其左孩子为2i+1,右孩子为2*i+2;其父节点为(i-1)/2。
具有n个节点的完全二叉树的深度为向下取整(logn)+1,即向下取整(log2*n),即向上取整log(n+1)
整数向上取整,向下取整都是他自己。
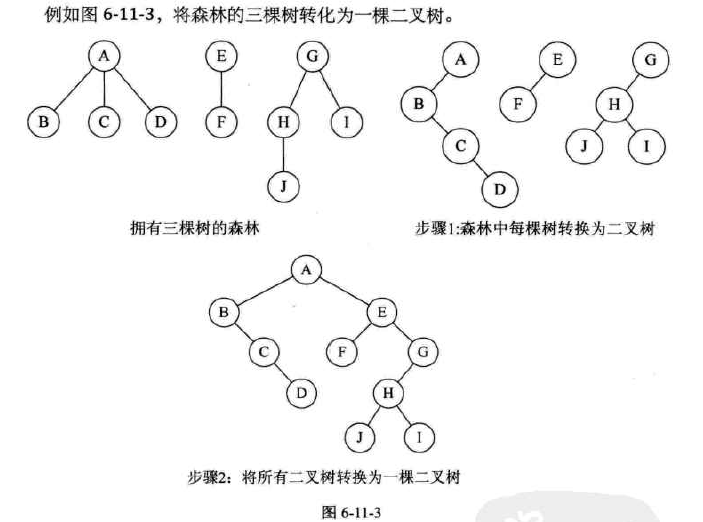
三、树与二叉树的转换
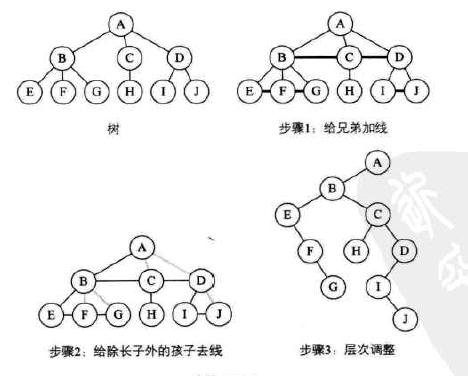
树转换为二叉树:
1.加线,在所有兄弟节点之间加一条线;
2.去线,对树中每个节点,只保留它与第一个孩子结点的连线,删除它与其他孩子节点之间的连线;
3.层次调整,第一个孩子是二叉树节点的做孩子,兄弟转换过来的孩子是节点的右孩子;
将一棵树转换为二叉树后形态是唯一的,且根节点没有右子树。
森林转换为二叉树:
1.把每个树转换为二叉树
2.第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根节点作为前一棵二叉树的根节点的右孩子,用线连接起来。
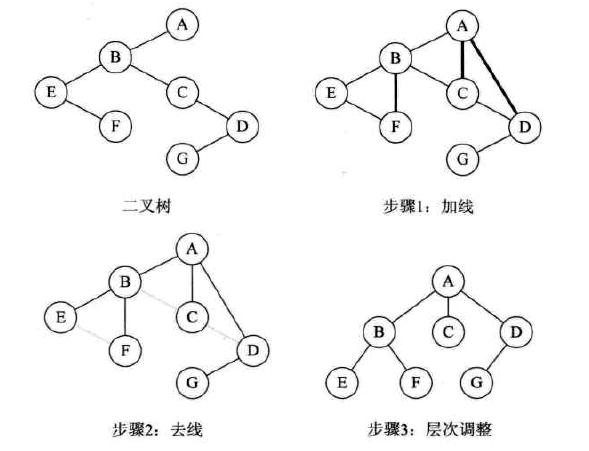
二叉树转换为树:
1.加线,若某个节点的左孩子存在,则将这个左孩子的右孩子节点,右孩子的右孩子节点。。。都作为此节点的孩子,将该节点与这些右孩子节点连接起来;
2.去线,删除原二叉树中所有节点与其右孩子节点的连线
3.层次调整。
二叉树转换为森林:
判断一棵树能够转换为一棵树还是森林,只要看这棵二叉树的根节点有没有右孩子,有就是森林,没有就是一棵树。
1.从根节点开始,若右孩子存在,则把与右孩子的连线删除,再查看分离后的二叉树,若右孩子存在,则连线删除...
2.每棵分离的二叉树转换为树即可。
树的遍历:
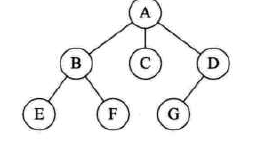
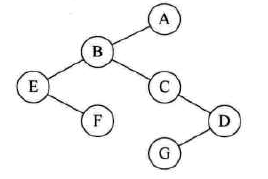
前序遍历:先访问树的根节点,然后依次前序遍历根的每棵子树;
后序遍历:先后序遍历每棵子树,然后再访问根节点。
上图(左)的前序遍历为ABEFCDG,后序遍历为EFBCGDA。
树的先根遍历,森林的先序遍历和二叉树的先序遍历相互对应。
树的后根遍历,森林的中序遍历和二叉树的中序遍历相互对应。
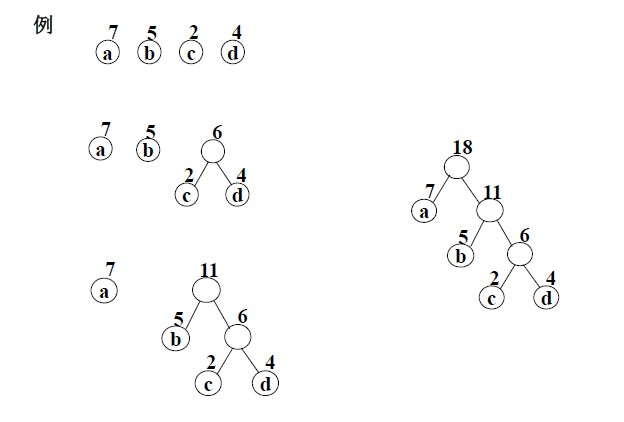
霍夫曼树
也叫最优二叉树,指的是带权值最小。
早都学过,这里直接放图:
霍夫曼树中所有节点度数要么为0,要么为2。
只有叶子节点才可以编码。2度节点数为107,叶子节点树为108。