差分隐私

差分隐私的由来

  想要在一个统计数据库里面保护用户的隐私，那么理想的隐私定义是这样的：访问一个统计数据库而不能够泄露在这个数据库中关于个人的信息。也就是说统计数据库应该提供一个统计值，但是对于个人的信息不应该被查询到。

  但是，这个理想的定义是不可行的，它并没有考虑到辅助信息。比如这么一个例子：一个关于某个地区女性的身高的数据库。可以从数据库当中查询到平均值，另外你根据辅助信息知道Alice的身高比平均身高高2cm，那么你就可以得到Alice的身高，即Alice身高信息被泄露了。

  我们退而求其次，用一种隐私保护比较弱，但是很实用的方法来定义隐私：一个人隐私泄露的风险不应该因为这个人的信息加入统计数据库而增加。这个定义就是差分隐私。

差分隐私的定义

  给定一个随机算法K，若对于任意的兄弟表$T_1$和$T_2$，以及任意的输出$S\subseteq Range(K)$ 满足:

$Pr[K(T_1) \in S] \leq  e^{\epsilon} \times Pr[K(T_2) \in S]  $

即：$\frac{Pr[K(T_1)\in \ S]}{Pr[K(T_1)\in \ S]} \leq e^{\epsilon}$

则算法K满足$\epsilon$差分隐私。下面我来解释这个定义：

首先是算法K，这是一个随机算法，随机算法意味着算法的输出是随机的，那么描述它就用概率里面的知识，比如概率密度函数，算法的输出概率等。

$T_1$和$T_2$是兄弟数据表，意味着数据表里面只相差一个记录，即一个数据表里面存在用户的信息，另外一个表里面不存在用户的信息。这是为了和上面的隐私定义相对应的，一个人的隐私泄露风险不应该因为这个人的信息在数据库中而增加。

$S\subseteq Range(K)$ 而不是$S = Range(K)$，是因为在概率密度函数为了确定一个事件的概率，应该用一个范围，而不是用一个点，在一点的概率总是0，这里表示的是输出在一个范围。

所以上面函数用概率的方法来进行度量，保证了在K在兄弟表上面，所有范围内的输出都很接近。

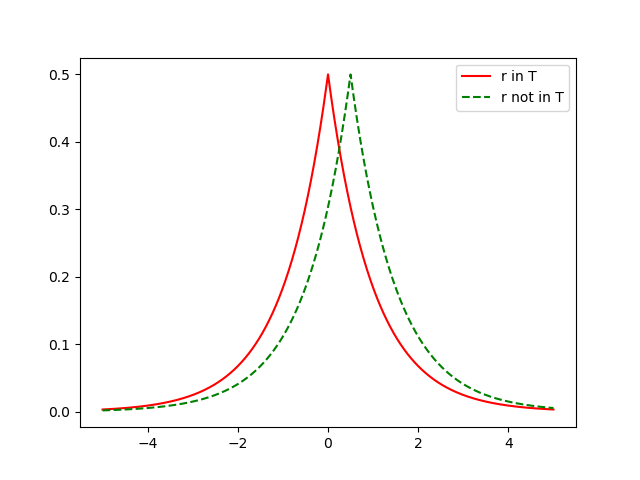
比如下面的Laplace分布，那么必须保证在整个算法的分布上面，两个数据表的输出都十分的接近，

敏感度

  隐私度是衡量一个函数的指标。对于一个函数$f: D \rightarrow R^d$，其中D是数据库，函数在数据库上面进行查询，返回一个d维矢量，L1敏感度定义如下：

  $S(f) = \max \limits_{D_1, D_2} {\Vert f(D_1) – f(D_2) \Vert }_1$

当函数f返回的结果是一个数字的时候，即$f: D \rightarrow R$，那么L1敏感度为：

  $S(f) = \max \limits_{D_1, D_2} \vert f(D_1) – f(D_2) \vert $

比如查询函数：满足特定条件下的记录有多少条。那么这个函数返回的结果是一个数字，它的敏感度$S(f) \leq 1$，即：当查询结果当中没有一条满足的时候，查询的敏感度为0，当有一条或者多条满足的时候，敏感度为1。

拉普拉斯噪声当中$\lambda 、\epsilon  和S(f) $的关系

让我们再来解释一遍这三个参数 $\lambda$是拉普拉斯分布里面的重要参数，决定和分布的方差

$\epsilon$ 是差分隐私定义中用来控制隐私度的一个度量

$S(f) $是我们定义的函数的敏感度

我们知道函数f在数据库D上面的输出为f(D),加上拉普拉斯噪声以后的概率密度为 $\frac{1}{2\lambda} exp(- \frac{\vert x-f(D)\vert}{\lambda})$.

那么它在一点a，取得的概率和该点的概率密度成正比，$Pr[K_f(D) =a] \propto exp(- \frac{\vert f(D)-a\vert}{\lambda})$

其中$K_f(D)$表示的是，函数f在数据D上面的输出经过随机函数K处理以后的值。

那么对于兄弟数据库D和D’,有$\frac{Pr[K_f(D_1) =a] }{Pr[K_f(D_2) =a] } = \frac{ exp(- \vert f(D_1)-a\vert / \lambda) }{exp(- \vert f(D_2)-a\vert / \lambda)} = exp( \frac{ \vert f(D_2)-a\vert - \vert f(D_1)-a\vert  }{\lambda} )$

那么根据绝对值不等式（三角不等式？）$\lvert a \rvert – \lvert b \rvert \leq \lvert a – b \rvert$，可以得到

$exp( \frac{ \vert f(D_2)-a\vert - \vert f(D_1)-a\vert  }{\lambda} ) \leq  exp( \frac{\lvert  f(D_1) – f(D_2) \rvert  }{\lambda} )  = exp( \frac{S(f)  }{\lambda} )$

可以看出来，若函数f加上参数为$\lambda$的拉普拉斯噪声，可以满足$\frac{S(f)}{\lambda}$的差分隐私，

同理，若函数f加上参数为$\frac {S(f)}{\epsilon}$的拉普拉斯噪声，可以满足$\epsilon$的差分隐私，

直方图差分隐私

  直方图的特点是这样的：所有的数据划分为等宽的方格，修改数据库里面的一条记录只会影响到一个方格内部的数据，所以直方图的查询敏感度为1。因此在直方图发布的时候直接加上$1/\epsilon$的拉普拉斯噪声就可以满足$\epsilon$的差分隐私。