开个新坑, 准备学习算法(第四版), 并把上面学到的东西写成博客, 毕竟以前也学过一点算法, 但效果甚微
并查集, 在这本书的第一章1.5中叫做union-find算法, 但在其他地方这个叫做并查集,就是说一系列点的连通问题,比如, 我们有十个点, 分别记作0~9:
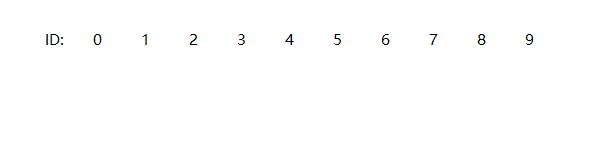
加入我们要把2和4连接起来怎么表示呢? 首先我们会想到,给所有的点标上一个号, 来代表他们的连通关系, 我们初始化这个数就是他们id本身:
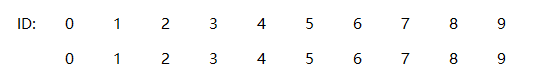
如果我们要连接2和4, 就使得4的id为2:

之后要连接间隔点任意两个点, 就把它们和它们相应的点的值都设置为一样就行了, 如果我们要比对这两个是是否连通, 也只要比较他们的值是否相等就行了.
我们可以很轻易的写出下面的代码:
1 /* 2 * 并查集实现程序 3 */ 4 public class UF { 5 private int[] id; 6 private int count; //连通图的个数 7 8 public UF(int N) { // 构造方法 9 id = new int[N]; 10 for(int i = 0; i < N; i++) { 11 id[i] = i; 12 } 13 count = N; 14 } 15 16 public void union( int p, int q) { // 连接两个点 17 int pId = find(p); 18 int qId = find(q); 19 if(pId == qId) // 已连接则不执行任何操作 20 return; 21 for(int i : id) { 22 if(id[i] == pId) 23 id[i] = qId; 24 } 25 count--; // 连通图数减1 26 } 27 28 public int find(int i) { // 查找点i所在分量的标识符 29 return id[i]; 30 } 31 32 public boolean connected(int p, int q) { // 查看亮点是否连通 33 return find(p) == find(q); 34 } 35 36 public int getCount() { // 获得连通图的个数 37 return count; 38 } 39 40 }
这就是树上的quick-find算法. 但是, 问题来了, 这样我们查找两个点是否连通很方便, 速度很快, 但是连接两个点就很慢了--我们需要遍历所有的点! 在例子中我们只有十个点, 可是若有几百万个点呢? 每操作一次就遍历上百万个点, 这样我们的代码肯定就会无比的慢, 所以, 我们必须想新的办法.

这是, 我们有了新的方法,就是书上的quick-union算法, 就是说, 我们每次连接两个点时, 只改变一个点的标识值, 也就形成了一棵棵树, 这样在一个连通图中就肯定有一个值的标识值是它本身的id, 没有发生改变, 当我们用查找find()方法查找时,只要一直往下找, 直到找到标识值为它本身的这个点就行, 这样就不会每次都遍历到所有的点, 总体上来说时间复杂度就降下来了:

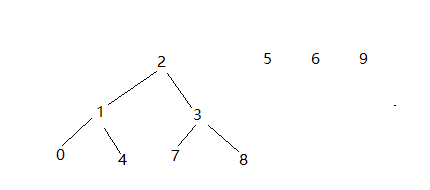
我们也可以轻易地写出相应的代码:
1 public void union( int p, int q) { // 连接两个点 2 int rp = find(p); 3 int rq = find(q); 4 if(rq == rp) 5 return; 6 if(sz[rp] < sz[rq]) { 7 id[rp] = rq; 8 sz[rq] += sz[rp]; 9 } else { 10 id[rq] = rp; 11 sz[rp] += sz[rq]; 12 } 13 count--; 14 } 15 16 public int find(int i) { // 查找该点的根节点 17 while(id[i] != i) 18 i = id[i]; 19 return i; 20 }
但是, 还不够, 因为我们得考虑最坏的情况, 就是当我们形成的这棵数没有分支, 也就是形成了一条链时, 我们就依然变成了需要遍历所有的点, 这样, 我们辛辛苦苦降下去的佛咋读有回来了

然后, 我们就有了书上的加权的quick-union算法, 就是将树的高度记录下来, 然后每次union()时把高度低的数加到高度高的树上去, 这样树的高度就不会超过lgN, 时间复杂度也控制在了O(lgN), 代码如下:
1 /* 2 * 并查集实现程序 3 */ 4 public class UF { 5 private int[] id; 6 private int count; //连通图的个数 7 private int sz[]; 8 9 public UF(int N) { // 构造方法 10 id = new int[N]; 11 sz = new int[N]; 12 for(int i = 0; i < N; i++) { 13 id[i] = i; 14 sz[i] = 1; 15 } 16 count = N; 17 } 18 19 public void union( int p, int q) { // 连接两个点 20 int rp = find(p); 21 int rq = find(q); 22 if(rq == rp) 23 return; 24 if(sz[rp] < sz[rq]) { 25 id[rp] = rq; 26 sz[rq] += sz[rp]; 27 } else { 28 id[rq] = rp; 29 sz[rp] += sz[rq]; 30 } 31 count--; 32 } 33 34 public int find(int i) { // 查找根节点 35 while(id[i] != i) 36 i = id[i]; 37 return i; 38 } 39 40 public boolean connected(int p, int q) { // 判断两个点书否连接 41 return find(p) == find(q); 42 } 43 44 public int getCount() { 45 return count; 46 } 47 48 }
当然, 我们再有办法优化, 我们的目标当然是无限接近常数次操作, 也就是O(1), 虽然这是不可能的. 那么, 我们还能怎么优化呢? 这就是,路径压缩, 就是说在调用find()方法时同时加一个循环, 将所有的这些点直接指向根节点, 这样我们下次操作这些点不就是常数次操作了嘛! 代码如下:
1 public int find(int i) { // 查找根节点 2 while(id[i] != i) 3 i = id[i]; 4 int j = i; 5 while(id[j] != j) { 6 int tmp = j; 7 j = id[j]; 8 id[tmp] = i; // 将其直接与根节点相连 9 } 10 return i; 11 }
在最后, 附送下最后的完整代码:
1 /* 2 * 并查集实现程序 3 * 使用路径压缩的加权quit-union算法 4 */ 5 public class UF { 6 private int[] id; 7 private int count; //连通图的个数 8 private int sz[]; 9 10 public UF(int N) { // 构造方法 11 id = new int[N]; 12 sz = new int[N]; 13 for(int i = 0; i < N; i++) { 14 id[i] = i; 15 sz[i] = 1; 16 } 17 count = N; 18 } 19 20 public void union( int p, int q) { // 连接两个点 21 int rp = find(p); 22 int rq = find(q); 23 if(rq == rp) 24 return; 25 if(sz[rp] < sz[rq]) { 26 id[rp] = rq; 27 sz[rq] += sz[rp]; 28 } else { 29 id[rq] = rp; 30 sz[rp] += sz[rq]; 31 } 32 count--; 33 } 34 35 public int find(int i) { // 查找根节点 36 while(id[i] != i) 37 i = id[i]; 38 int j = i; 39 while(id[j] != j) { 40 int tmp = j; 41 j = id[j]; 42 id[tmp] = i; // 将其直接与根节点相连 43 } 44 return i; 45 } 46 47 public boolean connected(int p, int q) { 48 return find(p) == find(q); 49 } 50 51 public int getCount() { 52 return count; 53 } 54 55 }
完成!