以前一直对MATLAB中fft()函数的使用一直存在疑惑,为什么要加一
些参数,并且如何确定这些参数,也查了许多资料,但很多都感觉只是
表面一说根本没有讲清其本质。但随着学习的推进,慢慢有所领悟,所
以打算把自己的一些所懂分享下,有什么问题也希望大家指正。
本文主要先对DFT、FFT的一些概念进行介绍,然后通过MATLAB仿真
进行fft()分析,从而解释上述参数。
一、DFT与FFT
首先是对DFT与FFT的一些概念上的介绍,其实FFT与DFT是等价的,他们实现的功能是一样的,只是FFT是DFT的算法优化,因为毕竟要用电脑来计算,DFT算的太慢了,就优化下也就成了FFT。所以此处我们对DFT与FFT的介绍是等价的。
那么我们就来介绍DFT,它也被叫做离散傅里叶变换,其实它就是DFS离散傅里叶级数的时域频域主值序列,或者也是DTFT离散时间傅里叶变换的频域采样。至于DFS与DTFT相信大家也是明白,那么很多人好奇为什么还要DFT这玩意,主要呢,还是因为计算机,因为计算机不可能处理无限长的信号而DFS和DTFT要么时域无限长,要么频域无限长,所以就搞了个DFT。
好的,那么我们就来直接看公式(这里我就假想大家都对其来源及原因都清楚了):
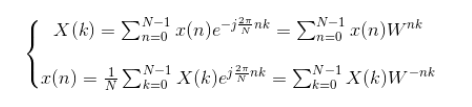

注意看上图,这就是我们接下来的所有依据,X(k)是正变换,x(n)反变换,此处务必注意x(n)那个式子有个1/N,这对后面的理解很关键。
好的那么接下来我们就可以利用MATLAB来进行分析了。
二、MATLAB的FFT函数使用
首先说明下什么情况下我们要用FFT,这是很简单的,但还是要说说:因为现实世界都是连续的信号,相信我们要分析它时单纯靠我们人算是很麻烦的,所有这些都是需要计算机进行计算,那么答案就有了,我们其实都是处理连续信号,也就是说我们都是想要FFT来分析连续信号。
OK
1、那么这样FFT第一个步骤就出现了,那就是A/D转换,也就是对连续信号采样。而这里我们就要确定一个参数采样频率Fs,说到采样,大家肯定会想到采样定理,其内容就是当对信号进行以采样频率为Fs>=2fc的采样时,信息不急丢失(fc为原始连续信号的最大截止频率),那么这样第一个参数Fs就这样确定了,其应该满足Fs>=2fc,这时采样周期为Ts=1/Fs。
2、既然确定了采样频率Fs,那么我们就要想信号的时域应该怎么确定,换句话说,我们将采样好的信号给计算机处理时,应该给计算机多少个。这里就出现了第二个参数即序列个数L,好的,在这里由于第一个参数确定的Fs,相应的也是采样周期Ts,所以我们就可以得出时域信号的横坐标时间的变化范围,也就是
t=(0:L-1)Ts
那么这里就确定了N吗?不,我们这里还没确定,对于L的确立我们需要上面这个语句的帮助。那么究竟怎么确定呢,这里我们就要想到DFT的来源了:为什么DFT可以用来进行表示信号的频谱响应,因为其时域频域都是信号的相应时域频域的主值区间,所以说我们要用DTF可以表示这个信号时,应尽可能的包含这个信号的一个周期或整数倍周期也就是上述t的范围应该是信号的一个周期范围或整数倍周期范围,否则则会发生频谱泄露,至于频谱泄露其实就是出现了本来没有的频率分量。比如说,10Hz的cos(2π10t),本来只有一种频率分量f=10Hz,但分析结果却包含了与10Hz频率相近的其它频率分量。下述将会进行仿真分析。所以说此处L的确定应是LxTs=mT(T为信号的最小周期,m为正整数),常常m=1。那么或许有人问怎么平常我看到的都不是这样,L都是取和Fs一样的值(注意为了频率分辨率为1Hz,下文会讨论)。其实对于这个也有它的道理,不妨我们推到下:
LxTs=L/Fs=1,也就是说其表达的时域t范围为1,那么平常我们的信号最小周期一般都小于1的,要是当信号最小周期大于1时其就是错误的啦,所以这个只是对大部分来说是有用的。
那么说了这么多究竟怎么确定,要是按LxTs=mT确定会不会太麻烦,确实有时我们真的不能知道确定的信号最小周期,所以这里就放宽点,只要保证LxTs>=T就可以,当然如果可以取整数倍就最好了。
OK
可是上面说又会发生频率泄露,这可怎么办?那么这里就只能尽可能提高N-DFT的N点啦,这样能使尽可能更多的能量落到正确的频率点上,也就是说这样误差会更小,这样就能达到我们的目的。
3、于是第三个参数N-DFT的N就出现了,根据上述2情况,我们知道N的提高有利于提高精确的,那么它还有其它约束吗?答案肯定有的,这里就需要些理论知识了:
先来了解下频域采样定理:频域以N点为采样周期的采样,在时域就是原序列的以周期N的延拓。
那么这样也就是说上述2中的序列长度L必须小于或等于N,否则就会发生时域混叠,所以说L>=N这就是限制条件,常常我们取L=N,当发生频谱泄露比较严重时我们就可以考虑将L增大,这样就可以减小频谱泄露的的影响。
综上,以上就是MATLAB相关的所有参数了,它们分别就采样频率Fs,原序列长度L,N-DFT变换的N,其主要确定关系总结如下:
Fs>=2fc(fc为信号最高截止频率)
LxTs>=T(T为信号的最小周期,若能取LxTs=T则应尽可能取,可以避免频谱泄露)
N>=L(N常常应为2^m,因为FFT运算就是不断模2进行DFT,所以N为2的次方利于提高速度)
对于其常取值,Fs=1024,N=1024,L=1024,注意满足上述条件就好
说完了这些参数,我们就讲讲MATLAB的fft函数,其用法主要Y=fft(x,N),x为原信号序列,Y为DFT(也就是FFT)变换后的,但是大家会发现其变换后幅度变了而且变了很大,其实就是跟最初的那个式子有关,其频域幅值增大了N倍。
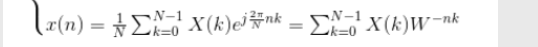
并且发现其横轴也都是整数,所以这时也要对其横轴坐标进行变换,即要乘以相应的频率分辨率Fs/N,所以说上面为什么,常常也取Fs=L,N=L,这样为了频率分辨率为1Hz,对于这些我们需用以下MATLAB语句进行实现
Y=fft(x,N);%N一定到大于信号序列x的长度,不过一般等于,决不能小于
%因为若要小于时域就会发生混叠
Y=abs(Y);
Y=Y./N;
%Y=Y.*2./N;Y(1)=Y(1)./2;若考虑将负频率的幅度折算到正频率时应这样处理
%因为变换后有个N的乘积因子的影响,根据DFT公式可知,故消除其影响
f=(0:N-1)*Fs./N;
%频率正常化,因为变换后横坐标是每个点对应的个数,故应转化成实际的频率
%由于频谱是对称的,且周期的故常常只画一半如下
subplot(2,1,1);
plot(f(1:N/2),Y(1:N./2));
%当然也可以画平常我们见到的有对称的如下
f=f-Fs./2;
subplot(212);
plot(f,fftshift(Y));
上述代码也有相关解释,那么我也就对相关几个语句进行介绍解释:
f=(0:N-1)*Fs./N;这是N-DFT变换后的横轴坐标,也就是真实频率值;
Y=Y./N;这是对DFT变换后幅值处理,也就是要除于N才是真实的幅值
%Y=Y.*2./N;Y(1)=Y(1)./2;而这个是鉴于无真实的负频率,其与正频率对称的原理,把负频率去掉,全变为正频率的幅值处理。
下面语句是为了变成我们平常看到有正负频率的图像
f=f-Fs./2;
subplot(212);
plot(f,fftshift(Y));
三、仿真试验
OK接下来就是仿真试验啦。
我们直接考虑x(t)=cos(2π10t);其周期T=0.1s,fc=10Hz
1、首先考虑Fs=512,L=512,N=512,满足上述三个关系吧,
Fs=512>=2fc;LxTs=1s>=T(也是10T,故没频率泄露);N=512>=L=512;那么我们看下仿真结果是否对得到:

可以看到只有一个频率,可以完全表示,故与上述推理一样。代码如下
Fs=512;%采样频率
Ts=1/Fs;%采样周期
N=512;%N—DFT
L=512;%原信号序列长度
t=(0:L-1).*Ts;%时域自变量
x=cos(10*2*pi*t);%原信号
subplot(311);
plot(t,x);
title("原信号")
xlabel("t/s")
grid on
Y=fft(x,N);%fft变换
Y=abs(Y)./N;%实际幅值变换
f=(0:N-1)*Fs./N;%实际频率变换
subplot(312);
plot(f(1:N/2),Y(1:N./2));
title("N-DFT变换幅频响应单边")
xlabel("f/Hz")
grid on
f=f-Fs./2;%移位
subplot(313);
plot(f,fftshift(Y));%移位
title("N-DFT变换幅频响应双边")
xlabel("f/Hz")
grid on
2、那么我们再来考虑Fs=512,L=128,N=128,满足上述三个关系吧,
Fs=512>=2fc;LxTs=0.15s>=T(不是T的整数倍,故有频率泄露);N=128>=L=128;那么我们看下仿真结果是否对得到(这次频谱用stem绘制更明显点):
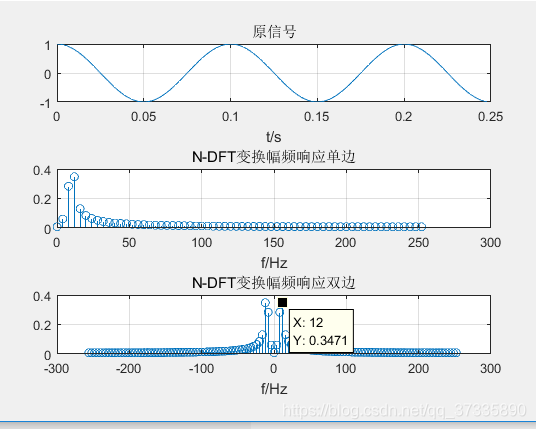
可以看到出现了些不应该出现的频率,也验证了我们的推论,其代码如下:
Fs=512;%采样频率
Ts=1/Fs;%采样周期
N=128;%N—DFT
L=128;%原信号序列长度
t=(0:L-1).*Ts;%时域自变量
x=cos(10*2*pi*t);%原信号
subplot(311);
plot(t,x);
title("原信号")
xlabel("t/s")
grid on
Y=fft(x,N);%fft变换
Y=abs(Y)./N;%实际幅值变换
f=(0:N-1)*Fs./N;%实际频率变换
subplot(312);
stem(f(1:N/2),Y(1:N./2));
title("N-DFT变换幅频响应单边")
xlabel("f/Hz")
grid on
f=f-Fs./2;%移位
subplot(313);
stem(f,fftshift(Y));%移位
title("N-DFT变换幅频响应双边")
xlabel("f/Hz")
grid on
3、那么我们再来看下增大N点是否可以减小频谱泄露的影响,考虑Fs=512,L=128,N=1024,满足上述三个关系吧,
Fs=512>=2fc;LxTs=0.15s>=T(不是T的整数倍,故有频率泄露);N=1024>=L=128;那么我们看下仿真结果是否对得到(这次频谱用stem绘制更明显点):
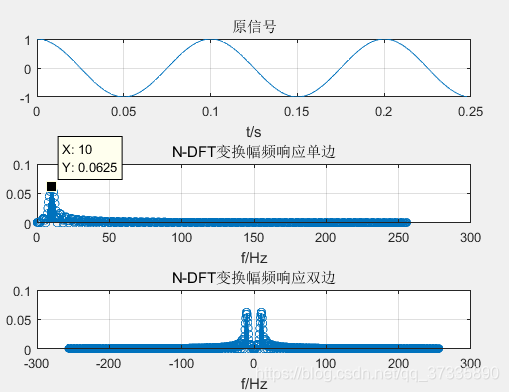
很明显可以看到与N=128时,其往所求正确频率处更靠近集中,故增大N可以减小频率响应的影响。代码如下:
Fs=512;%采样频率
Ts=1/Fs;%采样周期
N=1024;%N—DFT
L=128;%原信号序列长度
t=(0:L-1).*Ts;%时域自变量
x=cos(10*2*pi*t);%原信号
subplot(311);
plot(t,x);
title("原信号")
xlabel("t/s")
grid on
Y=fft(x,N);%fft变换
Y=abs(Y)./N;%实际幅值变换
f=(0:N-1)*Fs./N;%实际频率变换
subplot(312);
stem(f(1:N/2),Y(1:N./2));
title("N-DFT变换幅频响应单边")
xlabel("f/Hz")
grid on
f=f-Fs./2;%移位
subplot(313);
stem(f,fftshift(Y));%移位
title("N-DFT变换幅频响应双边")
xlabel("f/Hz")
grid on
4、最后看下它可不可ifft()变回去:

这是对于1的ifft只在后面加上下述代码:
figure
subplot(211)
plot(t,x)
title("原信号")
xlabel("t/s")
grid on
Y=fft(x);
xx=ifft(Y);
subplot(212)
plot(t,xx)
title("ifft原信号")
xlabel("t/s")
grid on
所以ifft变换时,应把一开始的N因子变回去。
对于非周期信号,其原理差不多,关键是时域能否尽可能取到一个周期等,或者对于无限长的信号,只能采取截取出其中最主要的信息了。
综上,差不多就这样了,可能多少有些问题,欢迎大家指正互相进步。