-
1 一维高斯分布
-
1.1 一维高斯分布的定义
若连续型随机变量X的概率密度为:
其中,
为常数,则称X服从参数为
,
的正态分布或高斯分布,记为
-
1.2 一维高斯分布的曲线
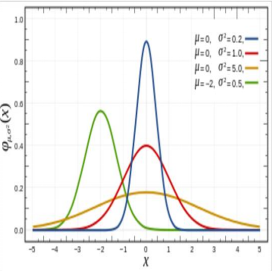
横轴表示可能的取值x,竖轴表示概率分布密度F(x),那么不难理解这样一个曲线与x轴围成的图形面积为1。因其曲线呈钟形,因此人们又经常称之为钟形曲线。正态分布的期望值决定了曲线的位置,标准差
决定了分布的幅度。
越大,则图形越宽,分布越分散,尖峰越小;
越小,则图形越窄,分布越集中,尖峰越大;
-
1.3 标准一维高斯分布
当,
时称随机变量X服从标准正态分布:
-
2 二维高斯分布
-
2.1 二维高斯分布的定义
二维高斯分布函数为X,Y两个方向的一维高斯函数的乘积:
根据二维高斯函数具有旋转对称性得出:
当时,二维高斯函数如下:
-
2.2 二维高斯分布的曲线
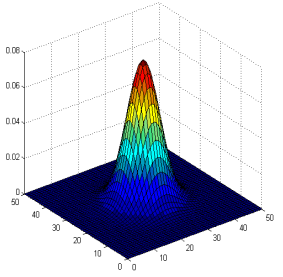
-
3 二维高斯滤波器
-
3.1 高斯滤波器简介
高斯滤波器是一种线性滤波器,能够有效的抑制噪声,平滑图像。其作用原理和均值滤波器类似,都是取滤波器窗口内的像素的均值作为输出。但其窗口模板的系数和均值滤波器不同,均值滤波器的模板系数都是相同的为1,而高斯滤波器的模板系数则随着距离模板中心的增大而减小。所以,高斯滤波器相比于均值滤波器对图像个模糊程度较小。
-
3.2 生成高斯滤波器模板(掩模)
要产生一个3×3的高斯滤波器模板,以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标,如下所示(x轴水平向右,y轴竖直向下)。
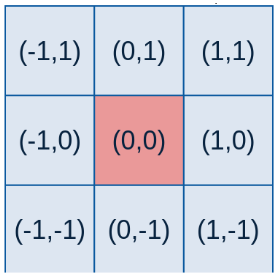
其中(x,y)为点坐标,在图像处理中可认为是整数,是标准差。将各个位置的坐标带入到高斯函数中,得到的值就是模板的系数,模板中各个元素值的计算公式如下:
当 =0.8时,计算出来的模板有两种形式:小数和整数
1)小数形式的模板,就是直接计算得到的值,没有经过任何的处理;
2)整数形式的模板需要进行归一化处理,即将模板左上角的值归一化为1。
取整后为:
使用整数的模板时,需要在模板的前面加一个系数,该系数为模板系数和的倒数,最终得到模板如下:
-
3.3
值的意义及选取
通过上述的实现过程发现,生成高斯滤波器模板最重要的参数就是高斯分布的标准差,标准差代表着数据的离散程度。
越小,模板的中心系数越大,周围的系数越小,这样对图像的平滑效果就不是很明显;
越大,模板的各个系数相差就不是很大,比较类似均值模板,对图像的平滑效果比较明显。
-
3.4高斯函数的五个性质
高斯平滑滤波器,无论在空间域还是在频率域都是十分有效的低通滤波器,高斯函数具有五个十分重要的性质:
(1)二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的。一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑。旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向。
(2)高斯函数是单值函数。这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的。这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真。
(3)高斯函数的傅里叶变换频谱是单瓣的。正如下面所示,这一性质是高斯函数的傅里叶变换等于高斯函数本身(但幅值和方差发生了变化,尤其是方差变为倒数)这一事实的直接推论。图像常被不希望的高频信号所污染(噪声和细纹理 )。而所希望的图像特征(如边缘),既含有低频分量,又含有高频分量。高斯函数傅里叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染,同时保留了大部分所需信号。
(4)高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的。σ越大,平滑程度就越好。通过调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折中。
(5)由于高斯函数的可分离性,大高斯滤波器可以得以有效地实现。二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同一维高斯函数卷积。因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长。