据说是腾讯的一个笔试题

小Q有X首长度为A的不同的歌和Y首长度为B的不同的歌，现在小Q想用这些歌组成一个总长度正好为K的歌单，每首歌最多只能在歌单中出现一次，在不考虑歌单内歌曲的先后顺序的情况下，请问有多少种组成歌单的方法。
输入描述:
每个输入包含一个测试用例。
每个测试用例的第一行包含一个整数，表示歌单的总长度K(1<=K<=1000)。
接下来的一行包含四个正整数，分别表示歌的第一种长度A(A<=10)和数量X(X<=100)以及歌的第二种长度B(B<=10)和数量Y(Y<=100)。保证A不等于B。

某某用python写的程序是这样

k = int(input().strip())
lx, x, ly, y = list(map(int, input().strip().split(" ")))
  
dp = [1] + [0] * k  # 第一位初始化为1
for i in range(x):
    for j in range(k, lx-1, -1):
        dp[j] += dp[j-lx]
          
for i in range(y):
    for j in range(k, ly-1, -ly):  # 第二次步长为ly
        dp[j] += dp[j-ly]
print(dp[k]%1000000007)

以下为分析

这个程序猿应该是把这个问题想象成一个杨辉三角的问题，杨辉三角有个例子是寻找A到B的线路，从A走到K，总共有多少种走法的问题，线路是一个杨辉三角

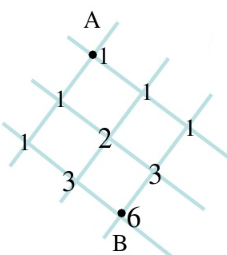
                        1（A）
                   1            1
                 1         2           1
             1         3        3（C）       1
          1      4         6（K）       4        1

比如从A走到C就一共有三种走法，从A到B一共六种走法（只能从上往下走）
那么这个问题，就这样考虑：
先假设都是长度为A的歌，一共有X首，那么这些歌可以表示成x1,x2,x3,x4,x5...xn(n=X)
用这X首歌去组成一个时长K，这些x1,x2,...xn就像地图上的路径

                          1（A）
                   1(E)         1(F)
                 1        2          1
             1         3      3（C）      1
          1      4        6（K）    4         1

如由A到E，可以看成x1,由A到F看成x2,依次类推
最终我们由起点A经过若干个xn到达K，而位置K上对应的数值，就是方法的数量
这里xn对应一个步长，K也对应一个数值：总距离

现在可以分析下作者的代码：
k = int(input().strip())
lx, x, ly, y = list(map(int, input().strip().split(" ")))

dp = [1] + [0] * k # 第一位初始化为1
print(dp)
for i in range(x):
for j in range(k, lx-1, -1):
dp[j] += dp[j-lx]
print(dp)

设k=50，xl=5，x=10
程序打印
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 3, 0, 0, 0, 0, 3, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 4, 0, 0, 0, 0, 6, 0, 0, 0, 0, 4, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 5, 0, 0, 0, 0, 10, 0, 0, 0, 0, 10, 0, 0, 0, 0, 5, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 6, 0, 0, 0, 0, 15, 0, 0, 0, 0, 20, 0, 0, 0, 0, 15, 0, 0, 0, 0, 6, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 7, 0, 0, 0, 0, 21, 0, 0, 0, 0, 35, 0, 0, 0, 0, 35, 0, 0, 0, 0, 21, 0, 0, 0, 0, 7, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 8, 0, 0, 0, 0, 28, 0, 0, 0, 0, 56, 0, 0, 0, 0, 70, 0, 0, 0, 0, 56, 0, 0, 0, 0, 28, 0, 0, 0, 0, 8, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 9, 0, 0, 0, 0, 36, 0, 0, 0, 0, 84, 0, 0, 0, 0, 126, 0, 0, 0, 0, 126, 0, 0, 0, 0, 84, 0, 0, 0, 0, 36, 0, 0, 0, 0, 9, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 10, 0, 0, 0, 0, 45, 0, 0, 0, 0, 120, 0, 0, 0, 0, 210, 0, 0, 0, 0, 252, 0, 0, 0, 0, 210, 0, 0, 0, 0, 120, 0, 0, 0, 0, 45, 0, 0, 0, 0, 10, 0, 0, 0, 0, 1]

上面那堆数字绝对是个杨辉三角，虽然dp是个一位数组，但是保存了K位置所在的行。k的位置必须有数值，否则就表示没有一种方法能组成正确的歌单。如上面的dp[K]=1,说明，拥有50首5分钟的歌，组成50分钟的歌单，只有一种方法。
即AX=5X=50，X=10，即只有拿出10首时长为5的歌来组这一种方法。如果时长为49，即dp[k]=49,那么就无解了

再考虑有“Y首长度为B”的情况

同样的思路，只是设想在杨辉三角中间，存在一个“步长”为ly的杨辉三角就好了。

据说是腾讯的一个笔试题

猜你喜欢