【排列组合】给定一个M*N的格子或棋盘，从左下角走到右上角的走法总数（每次只能向右或向上移动一个方格边长的距离）

解法1：我们可以把棋盘的左下角看做二维坐标的原点(0,0)，把棋盘的右上角看做二维坐标(m,n)(坐标系的单位长度为小方格的变长)   

用f(i, j)表示移动到坐标f(i, j)的走法总数，其中0=<i, j<=n，设f(m, n)代表从坐标（0,0）到坐标(m,n)的移动方法，

则f(m, n) = f(m-1, n) + f(m, n-1).

于是状态f(i, j)的状态转移方程为：

f(i, j) = f(i-1, j) + f(i, j-1)    if i, j>0

f(i, j) = f(i, j-1)                  if i=0

f(i, j) = f(i-1, j)                  if j=0

优化的状态f(i, j)的状态转移方程为：

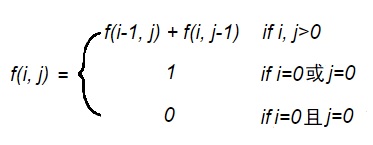
递归结束条件为：f(0,0)=0, f(0,1)=1, f(1,0)=1。这个问题可以在时间O(n^2)，空间O(n^2)内求解。

递归解法

1 //递归解法
2 int process(int m, int n) {
3     if (m == 0 && n == 0)
4         return 0;
5     if (m==0 || n==0)
6         return 1;
7     return process(m, n - 1) + process(m - 1, n);
8 }

View Code

非递归解法

 1 int processNew(int m,int n){
 2     int **Q=new int*[m+1];
 3     for(int i=0; i<=m; ++i){
 4         Q[i]=new int[n+1]();
 5     }
 6     //初始化
 7     Q[0][0]=0;
 8     for(int j=1; j<=n; ++j)
 9         Q[0][j]=1;
10     for(int i=1; i<=m; ++i)
11         Q[i][0]=1;
12     //迭代计算
13     for(int i=1; i<=m; ++i){
14         for(int j=1; j<=n; ++j){
15             Q[i][j]=Q[i-1][j]+Q[i][j-1];
16         }
17     }
18     int res=Q[m][n];
19     delete [] Q;
20     return res;
21 }

View Code

解法2：这个题目其实是一个组合问题。对方向编号，向上是0，向右是1，那么从左下角走到右上角一定要经过M 个1和N个0。这个题目可以转化为从M+N个不同的盒子中挑出M个盒子有多少种方法。答案是C(M+N, M)，或者C(M+N, N)的组合数。

---------------------------------------------------------------------------------------

版权声明：本文为CSDN博主「梵解君」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/hadeso/article/details/12622743