模拟滤波器到数字滤波器的映射方法

模拟滤波器到数字滤波器的映射方法

将已经设计好的模拟滤波器,通过一组映射关系变换为数字滤波器.对于这样一个映射来说,必须确保

1. 映射前后频率对应
2. 因果稳定的系统在映射后仍为因果稳定系统

以下是具体方法:

冲激响应不变法

从时域角度出发,使滤波器得单位冲激响应逼近模拟滤波器的单位冲激响应.为了实现这一目的,我们可以对模拟滤波器的冲激响应 $h(t)$进行采样,得到的离散序列即为滤波器的单位冲激响应.
$h(nT)=h_a(t)|_{t=nT}$

系统函数

根据时域推出s域的变换过程,设模拟滤波器的系统函数有N个一阶极点 $s_i$,那么其系统函数就可写为
$H_a(s)=\sum_{k=1}^N \frac{A_k}{s-s_k}$
变换到时域后,抽样所得离散序列为
$h(n)=h_a(nT)=\sum_{k=1}^N A_ke^{s_knT}u(n)$
等式取z变换求得原模拟滤波器所映射的数字滤波的系统函数
$H(z)=\sum_{k=1}^N \frac{A_k}{1-e^{s_kT}z^{-1}}$
这样看似完成了模拟滤波器的映射,但实际上我们需要注意到一点,或者说我们在设计的时候没有考虑到一点:抽样是否等价.这既是冲激响应不变法的核心,也是所来诸多问题的元凶.

借助于抽样信号频谱与原信号频谱之间关系
$H(e^{j\omega})=\frac 1T \sum_{k=-\infty}^\infty H_a(j\frac{\omega-2k\pi}{T})$
可以看出,抽样信号实际是原信号频谱的周期延拓且加权,所以在实际设计中,令 $h(n)=T h_a(nT)$来消除这一误差

缺点

仍然是由于冲激响应不变法的核心:抽样定理所带来的问题

1. 混叠失真

   我们知道,抽样定理仅适用于带限信号.而实际中,由于频域有限时域无限,这就导致不存在真正意义上的带限信号,通常在频域都是无限的.

   而从抽样定理中我们又知道,要想无失真的抽取信号,存在一个抽样频率的最小值.所以对于这样无限长频谱来说,使用给定抽样频率必然导致频谱混叠.

   需要说明的一点,这里增大抽样频率并不能改善混叠失真的情况.如果增大抽样频率,那么抽样周期T减小,而根据频率见映射关系 $\Omega=\omega T$可知,T的改变将影响模拟滤波器的参数,而在映射前,这两个滤波器的参数就已经被固定了.

   要想改善混叠失真现象,只能增大阻带衰减.只要衰减足够大,加叠多少分量都行.

2. 高通不可实现

   在上面提到过,抽样定理只能用于带限信号.对于像高通滤波器这样,通带为 $[\omega_p,\infty]$,自然是不可实现.除了高通之外,还有带阻滤波器不可实现

频率映射关系

s平面到z平面的映射关系为
$z=e^{sT}$
所以有
$\rho e^{j\omega} = e^{\sigma T}e^{j\Omega T}$
从模拟频率到数字频率之间的关系为线性
$\omega = \Omega T$

我们也可在映射关系这一角度上来说明混叠现象:

记 $s=\sigma+j\Omega$

当 $\sigma=0,\Omega\in(-\pi,\pi)$时,s将映射到z域单位圆上
当 $\sigma=0,\Omega\in(\pi,3\pi)$时,s仍映射到单位圆上

其实在这一映射关系下,s与z并不是一一对应的关系,而是多个s对应一个z,而滤波器的系统函数很显然在s域上并不是一个周期函数,所以这一映射必然不能完整的反应出原滤波器的特性.

双线性变换法

从频域角度出发,使得数字滤波器的频率响应逼近模拟滤波器的频率响应.

系统函数

从频域出发,找一个合适的映射关系,将s域映射到z域,从而实现数字滤波器的逼近设计

.在前文中提到过s到z映射的多值对应关系,因此解决这一问题,建立单值映射,从而避免频率响应的混叠失真.实现这一目的可以将原s域映射到 $\Omega\in(-\frac \pi T,\frac \pi T)$的平面s1上,再从s1平面建立单只映射到z域

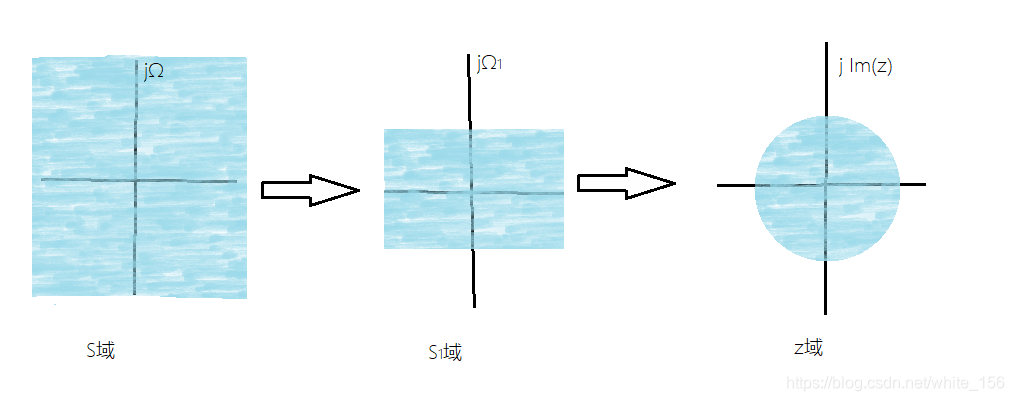
实现s域压缩采用如下变换
$\Omega = \tan(\frac{\Omega_1 T}{2})$
这样当 $\Omega\to \pm \infty$时,有 $\Omega_1 \to \pm \pi$,就可以实现压缩.将上式变形为
$j\Omega = \frac{\sin(\frac{\Omega_1 T}{2})}{\cos(\frac{\Omega_1 T}{2})} = \frac{e^{j\frac{\Omega_1 T}{2}}-e^{-j\frac{\Omega_1 T}{2}}}{e^{j\frac{\Omega_1 T}{2}}+e^{-j\frac{\Omega_1 T}{2}}}$
则有
$s=th[\frac{s_1 T}2]=\frac{1-e^{-s_1 T}}{1+e^{-s_1 T}}$
令 $z=e^{s_1 T}$将s1映射到z,就得到了s域到z域的映射关系
$s=\frac{1-z^{-1}}{1+z^{-1}} \\ z=\frac{1+z}{1-z}$
为了使AF和DF的某一频率有对应关系,可引入待定常数C.如果要求在零频附近有确切对应关系,则应取 $C=\frac 2T$.书上原话,为啥不知道,后面做题都用这个式子,什么鬼东西
$s=\frac 2T \frac{1-z^{-1}}{1+z^{-1}}$
因此所设计的数字滤波器的系统函数为
$H(z)=H_a(s)|_{s=\frac 2T \frac{1-z^{-1}}{1+z^{-1}}}$

关于双线性变换系统函数的推导还存在另一种简单易懂的方法:

首先引入微分方程到差分方程的转换:
$h'(t) = \frac{h(n)-h(n-1)}{T} \\ h(t)=\frac{h(n)+h(n-1)}{2}$

给定AF系统函数,写为联级形式 $H(s)=\sum \frac{A_k}{s-s_k}$,所以第k个子系统的时域输入-输出关系可知为
$y'(t)-s_k y(t)= A_kx(t)$
转换为差分方程有
$\frac{y(n)-y(n-1)}T -s_k \frac{y(n)+y(n-1)}2 = A_k \frac{x(n)+x(n-1)}2$
取z变换有
$\frac 1T [Y(z)-z^{-1}Y(z)]-\frac{s_k}2[Y(z)+z^{-1}Y(z)]=\frac{A_s}2 [X(z)+z^{-1}X(z)]$
可以得到该子系统的系统函数
$H_k(Z) = \frac{A_s}{\frac 2T \frac{1-z^{-1}}{1+z^{-1}}-s_k}$
对照s域内系统函数可知
$H_k(z)=H_k(s)|_{s=\frac 2T \frac{1-z^{-1}}{1+z^{-1}}}$

频率映射关系

s到s1的关系: $\Omega = \frac 2T \tan \frac{\Omega_1 T}{2}$
s1到z关系: $\Omega_1 T= \omega$

所以有
$\Omega =\frac 2T \tan(\frac \omega 2)$
由此可见,对于线性的平面映射关系,其频率映射关系却是非线性的.因此,在将DF参数转换为AF参数时,必须考虑这一非线性映射所带来的影响,也就时频率预畸.

缺点

双线性变换的缺陷主要由其非线性的频率映射造成.

频率的非线性映射,可以理解为坐标轴的不等收缩,在某一段内,收缩的快;在某一段内收缩的慢.,所以这样就会带来其函数图像的畸变:幅度响应由线性变为非线性,例如理想微分器的双线性变换.

但是对于分段常数函数,在双线性变换后仍为分段常数函数.虽然非线性映射对区间的收缩程度不同,但是分段常数函数在对应定于区间内值恒定,所以即时收缩,其响应还是直线不变,只不够跳变点坐标发生变化.这就是虽然双线性变换存在对幅频响应的畸变效应,但是仍可以用来设计滤波器的原因.

优点

双线性变换的优点同样也来自于这样非线性映射.

• 由于是单值映射,因此没有混叠产生
  后仍为分段常数函数.虽然非线性映射对区间的收缩程度不同,但是分段常数函数在对应定于区间内值恒定,所以即时收缩,其响应还是直线不变,只不够跳变点坐标发生变化.这就是虽然双线性变换存在对幅频响应的畸变效应,但是仍可以用来设计滤波器的原因.