模拟低通滤波器

留个坑，这几天就填

butterworth

又称最平幅度特性滤波器.

幅度平方响应

$|H_a(j\Omega)|^2 = \frac{1}{1+(\frac {\Omega}{\Omega_c})^{2N}}$
其中N为滤波器阶数, $\Omega_c$为低通滤波器的截至频率.

在这里我们注意到,对于给定的 $\Omega_c$来说,无论N的取值为何,只要 $\Omega=\Omega_c$,则一定有 $|H_a(j\Omega)|=\frac {1}{\sqrt {2}}$,以分贝来记,-3dB增益不变.
针对这一特性，我们可以得到关于butterworth的一个缺点.考虑如下滤波器,其通带衰减最大不能超过1dB,通带截至频率为 $f_p$.可以看到 $f_p$显然小于-3dB处频率 $f_c$,所以在 $(f_p,f_c)$这一区间内,对频率分量的振幅衰减缓慢增长,且最大衰减不会超过3dB,在 $f>f_c$处,才能达到迅速衰减.
所以,butterworth低通的带宽是有剩余的,或者说不能实现在通带截止频率后的快速衰减,尤其是对 $f_p\neq f_c$的情况来说.

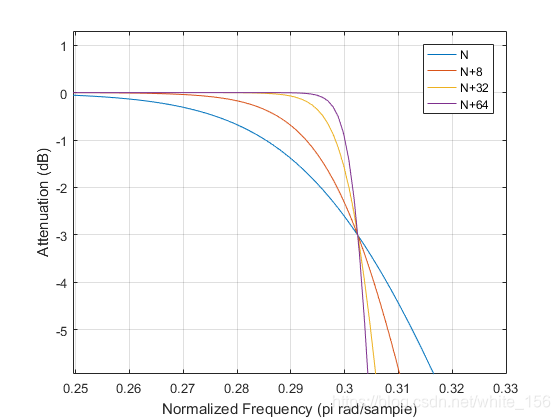
那么参数N又是控制什么的呢?N控制着滤波器的衰减特性.如下是matlab中的仿真

N越大,则通带内幅度特性越平坦,过渡带衰减越快.

归一化原型

为了方便于滤波器设计,是有一个系数表可供我们去查询的.但是这里的截止频率是归一化的,直白一点就是 $\Omega_c=1$.
所以要想查表,就必须先把所需的滤波器截止频率归一化,然后再去对应表中数据查找.
得到归一化的滤波器设计后,再去归一化,对横轴缩放,让截止频率移动到你想要的位置.
$H_a(s)=H_{an}(s')|_{s'=\frac{s}{\Omega_c}}=H_{an}(\frac{s}{\Omega_c})$

参数确定

$\Omega_p$为所需通带截止频率, $R_p$(dB)为 $\Omega_p$处 $|H_a(j\Omega_p)|$的衰减的最大值;
$-20\lg |H_a(j\Omega_p)| \le R_p \tag{1.1}$
$\Omega_{s}$为所需阻带截止频率, $A_{s}$(dB)为 $\Omega_{s}$处 $|H_a(j\Omega_{s})|$的衰减的最小值;
$-20\lg |H_a(j\Omega_s)| \ge A_s \tag{1.2}$
联立 $(1.1)$与 $(1.2)$得
$N \ge \frac {\lg \frac{10^{0.1A_s}-1}{10^{0.1R_p}-1}}{2\lg \frac{\Omega_s}{\Omega_p}}$
令 $\lambda_s=\frac{\Omega_s}{\Omega_p}$, $g=\sqrt{\frac{10^{0.1A_s}-1}{10^{0.1R_p}-1}}$,则
$N \ge \frac{\lg g}{\lg \lambda_s}$

确定N之后,根据 $\Omega_p$和 $\Omega_s$确定一个合适的 $\Omega_c$,使得选取的 $\Omega_c$能够满足在 $\Omega_p$处通过, $\Omega_s$处衰减.

• 如果 $R_p=3dB$
  则此时 $\Omega_p=\Omega_c$
• 若不等,则确定 $\Omega_c$的取值区间
  由 $(1.1)$与 $(1.2)$可推得
  $\Omega_c \ge \frac{\Omega_p}{ ^{2N} \sqrt{10^{0.1R_p}-1}} = \Omega_{cp} \\ \Omega_c \le \frac{\Omega_s}{ ^{2N} \sqrt{10^{0.1A_s}-1}} = \Omega_{cs}$
  故 $\Omega_{cp}\le\Omega_c\le\Omega_{cs}$

chebyshevⅠ

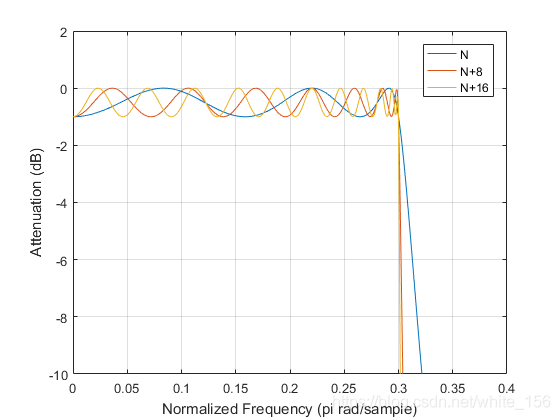
切比雪夫Ⅰ型滤波器在通带内是等波纹的,阻带内单调减.

幅度平方响应

$|H_a(j\Omega)|^2=\frac{1}{1+\varepsilon^2 G_N^2(\frac{\Omega}{\Omega_c})}$
$0<\varepsilon<1$为带通波稳参数, $\varepsilon$越大,波纹越大
$\Omega_c$为截止频率,表示幅度响应衰减到指定值时的截止频率.与butterworth滤波器不同,不特指3dB处频率
N为滤波器阶数,也等于通带内起伏波纹的极值数
$C_N(x)$为切比雪夫多项式

与butterworth相同的时,chebyshev在N变动时也存在定点.当 $\Omega=\Omega_c$时,无论N取何值,都有 $|H_a(j\Omega)|=\frac{1}{1+\varepsilon^2}$.因此,把 $\Omega_c$称为chebyshev的截止频率.

归一化原型

与butterworth一样,chebyshev也有其归一化的低通原型滤波器，其规定的 $\Omega_c=1$.在设计时,求得N与 $\delta_1$可查表得系数.之后做去归一化得到所需滤波器.
也可以根据如下公式求出系统函数得极点
$\gamma = \frac 1\varepsilon + \sqrt{\frac{1}{\varepsilon^2}+1} \\ a=\frac 12 (\gamma^{\frac 1N}-\gamma^{-\frac 1N}) \\ b=\frac 12 (\gamma^{\frac 1N}+\gamma^{-\frac 1N}) \\ s_k=-a\sin[\frac{\pi}{2N}(2k-1)]+jb\cos[\frac{\pi}{2N}(2k-1)]$
得到归一化系统函数
$H_{an}(s)=\frac{\frac{1}{\varepsilon 2^{N-1}}}{\prod_{k=1}^N (s-s_k)}$

参数确定

已知通带截止频率 $\Omega_c$及通带波纹 $\delta_1$；
阻带截止频率 $\Omega_s$及阻带波纹 $\delta_2$
$N\ge \frac{ch^{-1} [\frac 1\varepsilon \sqrt{10^{0.1\delta_2}-1}]}{ch^{-1} (\frac{\Omega_s}{\Omega_c})} \\ \varepsilon^2 = 10^{0.1\delta_1}-1$

chebyshev Ⅱ

也叫反向chebyshev滤波器.在通带内单调,阻带具有波纹特性

ellipse

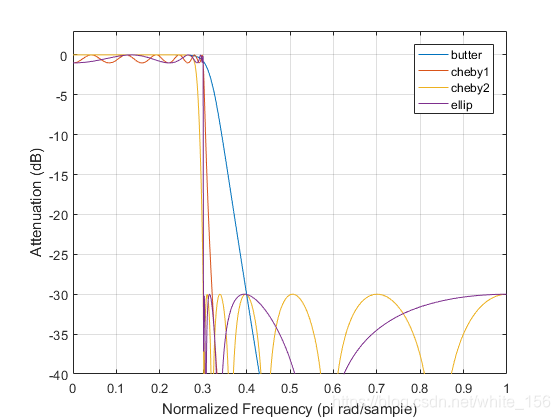
同一参数下，四类滤波器幅频响应比较

clear all
clc

fs=1e4;
Ts=1/fs;
fpass=3e3;
fstop=4e3;
Ap=1;
As=30;
Wp=fpass/fs;
Ws=fstop/fs;

[N,Wn]=buttord(Wp,Ws,Ap,As);
[butter_z,butter_p,butter_k]=butter(N,Wn);
sos = zp2sos(butter_z,butter_p,butter_k);
[butter_h,butter_w]=freqz(sos,1024);

[cheby1_z,cheby1_p,cheby1_k]=cheby1(N,Ap,Wp);
sos = zp2sos(cheby1_z,cheby1_p,cheby1_k);
[cheby1_h,cheby1_w]=freqz(sos,1024);

[cheby2_z,cheby2_p,cheby2_k]=cheby2(N,As,Wp);
sos=zp2sos(cheby2_z,cheby2_p,cheby2_k);
[cheby2_h,cheby2_w]=freqz(sos,1024);

[ellip_z,ellip_p,ellip_k] = ellip(N,Ap,As,Wp);
sos = zp2sos(ellip_z,ellip_p,ellip_k);
[ellip_h,ellip_w] = freqz(sos,1024);

figure
plot(butter_w/pi,20*log10(abs(butter_h)));
hold on
plot(cheby1_w/pi,20*log10(abs(cheby1_h)));
plot(cheby2_w/pi,20*log10(abs(cheby2_h)));
plot(ellip_w/pi,20*log10(abs(ellip_h)));
grid on
xlabel('Normalized Frequency (pi rad/sample)')
ylabel('Attenuation (dB)')
legend('butter','cheby1','cheby2','ellip')
axis([0 1 -40 3])