Foundation of machine learning

第7章 Boosting

集成方法是机器学习中的一种通用技术，可以去结合多个预测器来创建一个更准确的预测器。本章研究了一个被称为增强的重要集成方法家族，这个方法具体来说就是AdaBoost算法。该算法在某些场景中已经被实践证明是非常有效的，并且是基于丰富的理论分析。我们首先来介绍AdaBoost，展示下它如何通过快速减少轮数增强的经验误差，并指出它与一些著名算法的关系。接下来，我们来呈现出一种基于AdaBoost假设集的vc维数，并对AdaBoost的推广性质进行了理论分析，然后基于边际的概念，对其泛化性质进行了理论分析。在这种情况下发展的边际理论可以应用于其他类似的集成算法。而AdaBoost的博弈论可以进一步有助于分析其性质，揭示了弱学习假设与可分条件的等价性。

7.1 Introduction

这通常是困难的，对于一个不平凡的学习任务，去直接设计出一种满足第 $\mathcal 2$章强PAC学习要求的精确算法。但是，还是有很大的希望去找到仅能保证表现比随机稍好一些的简单预测器。下面给出了这种弱学习者的正式定义。正如在PAC学习的章节中一样，我们设 $\mathcal n$为一个数字，表示任何元素 $\mathcal x$∈ $\mathcal X$的计算代价最多为 $\mathcal O$( $\mathcal n$)，并用大小( $\mathcal c$)表示 $\mathcal c$ $\in C$计算表示的最大代价。

定义7.1（Weak learning）

如果存在一个概念类 $\in C$据说是弱PAC可学习的一个算法 $\mathcal A$， $\mathcal γ$>0，和一个多项式函数多聚（·，·，·），这样对于任何 $\mathcal δ$> $\mathcal 0$，对于 $\mathcal X$上的所有分布 $\in D$和任何目标概念 $\mathcal c$∈ $\mathcal C$，

AdaBoost( $\in S$= (( $\mathcal x_1, \mathcal y_1), . . . ,(\mathcal x_m,$ $y_m$)

---

for i $\leftarrow$to m do

$D_1(i)$ $\leftarrow$ $\frac{1}{m}$

for t $\leftarrow$ 1 to T do

$h_t$ $\leftarrow$ 基础分类器 $\mathcal H$ 误差小 $\epsilon_t$ = $p_i$~ $\mathcal D_t$[ $h_t$( $x_i$) $\neq$ $y_i$]

$a_t$ $\leftarrow$ $\frac{1}{2}$ log $\frac{1-\epsilon_t}{\epsilon_t}$

$Z_t$ $\leftarrow$ [ $\epsilon_t$(1- $\epsilon_t$)] $^{\frac{1}{2}}$ $\rhd$ 归一化[标准化]因数

for i $\leftarrow$ $\mathcal 1$ to m do

$\mathcal D_t$( $i$) $\leftarrow$ $\frac{D_t（i）exp（-a_ty_ih_t （x_t））}{Z_t}$

f $\leftarrow$ $\sum$ $^T _{t=1}$ $a_t$ $h_t$

return f

图7.1基本分类器集 $\mathcal H$⊆{−1，+1} $\mathcal x$的AdaBoost算法。以下算法适用于任何样本大小的 $\mathcal m$≥ $\mathcal poly$( $\mathcal 1$/ $\mathcal δ$， $\mathcal n$， $\mathcal size$( $\mathcal c$))：

其中 $h_S$是算法 $\mathcal A$在样本 $\mathcal S$上训练时返回的假设。当这样的算法 $\mathcal A$存在时，它被称为C的弱学习算法或弱学习者的算法。弱学习算法返回的假设称为基础分类器。 增强技术背后的关键思想是使用一个弱学习算法来建立一个强的学习者，也就是说，一个精确的PAC学习算法。要做到这一点，提升技术采用了一种集成方法：它们结合了弱学习者返回的不同基础分类器，以创建一个更准确的预测器。但是应该使用哪些基础分类器以及如何组合呢？下一节来通过详细描述一种最普遍和最成功的增强算法，AdaBoost来解决这些问题。

我们用 $\mathcal H$ 表示从中选择基本分类器的假设集，我们有时会称之为基分类器集。图7.1给出 图7.2

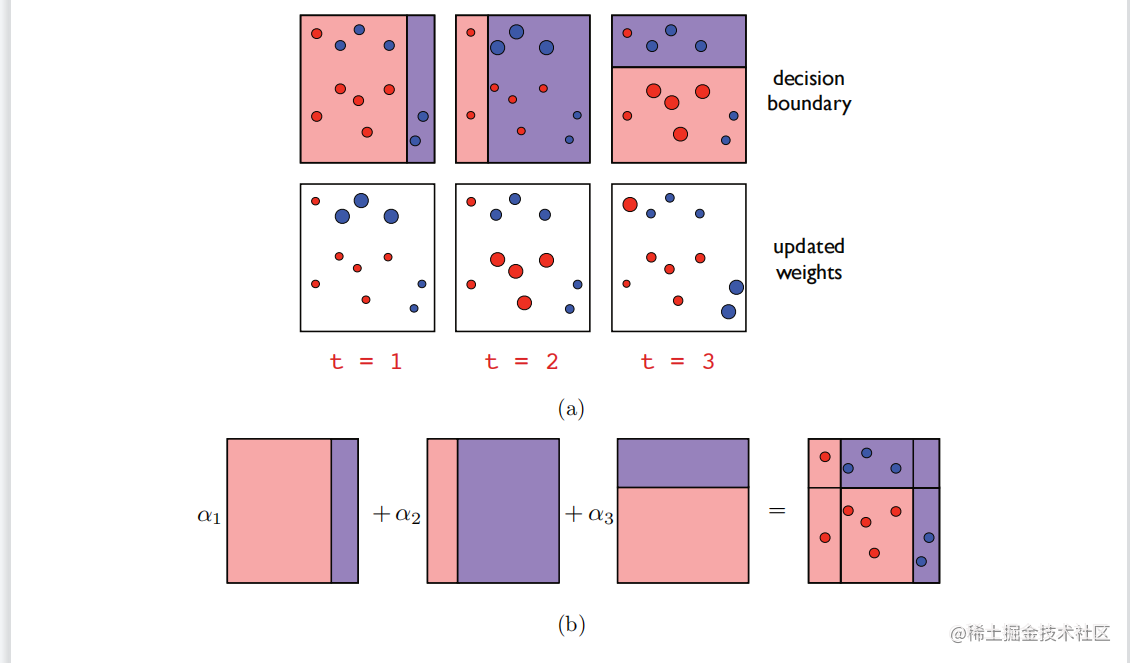以轴对齐的超平面作为基础分类器的AdaBoost示例。( $\mathcal a$)最上面的一行显示了每一轮推进时的决策边界。下面一行显示了每一轮如何更新权重，给出错误（正确）权重增加（减少）。( $\mathcal b$)最终分类器的可视化，构造为基分类器的非负线性组合。 在基分类器是从 $\mathcal X$映射到{ $\mathcal −1$， $\mathcal +1$}的函数时，AdaBoost的伪代码，因此 $\mathcal H$⊆{ $\mathcal −1$， $\mathcal +1$} $\mathcal X$。 该算法以一个标记的样本S=(( $x_1$， $y_1$)，…，( $x_m$， $y_m$))作为输入，其中，( $x_i$， $y_i$)∈X×{−1，+1}为所有的i∈{m}，并在索引{ $\mathcal 1$，…， $\mathcal m$}上保持一个分布。最初（第 $\mathcal 1$至 $\mathcal 2$行），分布是均匀的（ $\mathcal D1$）。在每一轮增强 $\mathcal h$时，即循环 $\mathcal 3$- $\mathcal 8$的每次迭代 $\mathcal t$∈{ $\mathcal i$}，选择一个新的基分类器 $\mathcal t$∈ $\mathcal H$，使由分布 $D_t$加权的训练样本的误差最小化：

$$h_{_t}\in\underset{h\in\mathcal H}{\argmin}\underset{i\sim\mathcal D_{_i}}{\mathbb{P}}[h(x_{_i})\neq y_{_i}]=\underset{h\in\mathcal H}{\argmin}\sum^{m}_{i=1}\mathcal D_{_t}(i)_{_{h(x_i)\neq y_i}}$$

$z_t$只是一个归一化因子,以确保权重 $\mathcal D_t$( $\mathcal i$)之和为 $\mathcal 1$。 定义系数 $\mathcal αt$的确切原因将在稍后变得清楚。

目前，观察到，如果 $\epsilon_t$基分类器的t的误差小于 $\frac{1}{2}$,这时 $\frac{1-\epsilon_t}{\epsilon_t}$ $\mathcal>$ 1 and $\mathcal a_\mathcal t$是积极的( $a_t$ $\mathcal >$ $\mathcal 0$).因此，新的分布 $\mathcal D_{t+1}$是从 $\mathcal D_t$通过大大增加它的重量 $\mathcal i$如果点 $\mathcal x_i$是错误的分类( $\mathcal y_i$ $\mathcal h_t$( $\mathcal x_i$)< $\mathcal 0$)，相反，如果 $\mathcal x_i$是正确分类的。这样做的效果是更多地关注下一轮助推中错误分类的点，而不是那些正确分类的点 $\mathcal h_t$

经过 $\mathcal T$轮增强后，AdaBoost返回的分类器是基于函数的符号进行的 $\mathcal f$，这是一个基分类器的非负线性组合 $\mathcal h_t$。重量 $\mathcal a_t$ 被分配给 $\mathcal h_t$在这个和中是精度之比的对数函数 $\mathcal 1$- $\epsilon_t$和错误 $\epsilon_t$ $\mathcal of$ $\mathcal h_t$.因此，更准确的基分类器在这个总和中被分配了一个更大的权重。图7.2说明了AdaBoost算法。这些点的大小表示在每一轮推进时分配给它们的分布权重。任何 $\mathcal t$ $\mathcal ∈$[ $\mathcal T$]，我们将用ft表示基分类器的线性组合 $\mathcal t$轮升力： $\mathcal f_t$= $\sum$ $^t _{s=1}$ $\mathcal a_s$ $\mathcal h_s$。特别是，我们有 $\mathcal f_T$= $\mathcal f$分布 $\mathcal D_{t+1}$可以用 $\mathcal f_t$归一化因素 $\mathcal Z_s$, $\mathcal s$∈[ $\mathcal t$]，如下：

$\forall$ $\mathcal i$∈[ $\mathcal m$], $\mathcal D_{t+1}$（ $\mathcal i$）= $\frac{e^{-y_if_t(x_i)}}{m \prod ^t_{s=1}Z_s}$ (7.2)

我们将在以下章节的证明中多次使用这个恒等式。它可以通过重复扩展点上分布的定义来直接显示出来 $\mathcal x_i$：

$\mathcal D_{t+1}$( $\mathcal i$)= $\frac{e^{-a_ty_if_t(xi)}}{Z_t}$= $\frac{\mathcal D_{t-1}（\mathcal i）e^{-a_{t-1}y_{i}h_{t-1}(xi)}e^{-a_ty_if_t(xi)}}{Z_{t-1Z_t}}$

= $\frac{e^{yi\sum^{t}_{s=1}a_sh_s(xi)}}{m \prod ^t_{s=1}Z_s}$

AdaBoost算法可以通过以下几种方式进行推广：

$h_t$可以不是加权误差最小的假设，而是由训练过的弱学习算法返回的基本分类器 $\mathcal D_t$;

基分类器的范围可以是[ $\mathcal −1$， $\mathcal +1$]，或者更一般地是一个有界的子集 $\R$

系数 $\mathcal α_t$可以不同，甚至可能不允许封闭形式。一般来说，选择它们是为了最小化经验误差的上界，如下一节所述。当然，在这种一般情况下，假设 $\mathcal h_t$不是二进制分类器，但它们的符号可以定义标签，它们的大小可以被解释为置信度的度量。

在本章的其余部分中， $\mathcal H$中的基分类器的范围将被假设包含在[ $\mathcal −1$， $\mathcal +1$]中。我们进一步分析AdaBoost的特性，并讨论其在实践中的典型应用。

7.2.1结合经验误差

我们首先证明了AdaBoost的经验误差随着助推轮数的函数呈指数快速减小.

定理7.2

AdaBoost返回的分类器的经验误差验证了： $\mathop{R}_s(\mathcal f$) $\leq$ exp $\lbrack$ $-2\sum\limits_{t=1}^{T} (\frac{1}{2}-\epsilon_t)^2\rbrack$
(7.3) 此外，如果为所有人 $\mathcal t$∈[T]， $\mathcal γ\le$( $\frac{1}{2}$- $\epsilon_t$),这时 $\mathop{R}_s$( $\mathcal f$) $\le$exp(-2 $\mathcal γ^2 T$).

证明：使用一般的不等式 $\mathcal 1_{u\leq0}$ $\le exp（-u）$对所有人都有效 $\mathcal u\in \mathbb R$和身份7.2，我们可以写道：

$\mathop{R}_s(\mathcal f$)= $\frac{1}{m}$ $\sum\limits^{m}\limits_{i=1}$