题解 of University of Central Florida 2020 (Fall) “Practice” Local Programming Contest
[by_041]
A. Vowel Count
Description
Dr. Orooji noticed that his name has more vowels than consonants. Since he likes meeting people like himself, he has asked you to write a program to help him identify such names.
Given a name, determine whether or not it has more vowels than consonants. Assume the vowels are “aeiou”.
Input
There is one input line, it contains a name. The name starts in column 1 and consists of 1-20 lowercase letters (assume the name will not contain any other characters).
Output
Print a 1 (one) or 0 (zero) indicating whether or not the name has more vowels than consonants.
Sample Input 1
ali
Sample Output 1
1
Sample Input 2
arup
Sample Output 2
0
Sample Input 3
travis
Sample Output 3
0
Sample Input 4
orooji
Sample Output 4
1
题解
- 字符串扫描
#include<bits/stdc++.h>
using namespace std;
int main()
{
string str;
int anss; //表示:元音数量-辅音数量
cin>>str;
for(int i=0,ii=str.size();i<ii;i++)
{
switch(str[i])
{
case 'a':case 'e':case 'i':case 'o':case 'u': //是元音
anss++;
break;
default: //不是元音(是辅音)
anss--;
break;
}
}
puts(anss>0?"1":"0"); //判断元音是否多于辅音
return 0;
}
B. Soccer Standings
Description
In a soccer match, a team either earns a win, tie or loss. A win is worth 3 points, a tie is worth 1 point, and a loss is worth 0 points. Unfortunately, due to poor record-keeping, some leagues have only saved the number of total matches played and the number of points each team has earned. One of these leagues has asked you to write a program to recreate the possible combinations of wins, ties and losses for a team in the league.
Given the number of games played by a soccer team in a season and the number of points earned by the team, list each possible combination of wins, ties and losses that the team could have gotten to achieve the given total points.
Input
There is one input line, it contains two space separated integers : g (0 < g ≤ 100)g(0<g≤100), and p (0 ≤ p ≤ 300)p(0≤p≤300), representing the number of games played and the total points earned by the team, respectively. It is guaranteed that there is at least one possible combination of wins, ties and losses that is consistent with the given information for the team.
Output
Print the possible records, each on a separate line with the format:
w-t-l
where w is the number of wins, t is the number of ties and l is the number of losses. Print these by descending order of wins.
Sample Input 1
6 10
Sample Output 1
3-1-2
2-4-0
Sample Input 2
1 3
Sample Output 2
1-0-0
Sample Input 3
4 4
Sample Output 3
1-1-2
0-4-0
题解
- 枚举
#include<bits/stdc++.h>
using namespace std;
int win;
void goo(int n,int m,int f=0) //还有有n场比赛没定,还需要m分,在录入第f个数据(win、tie、lose)
{
if(f) //如果是tie(win已经录入)
{
if(n>=m) //全是tie可以达到m分
{
printf("%d-%d-%d\n",win,m,n-m); //可以确定有一种可能的情况
}
return; //退回上层
}
for(int i=min((m/3),n);~i;i--) //在录入win,可能的值有0~min((m/3),n)
{
win=i; //录入一个win
goo(n-i,m-i*3,1); //在这个win下,录入下一个值(录入tie)
}
return;
}
int main()
{
int n,m;
cin>>n>>m;
goo(n,m); //总共n场比赛,得到m分
return 0;
}
C. Jumping Frog
Description
Freddy the frog is trying to go get a bite to eat. The problem is Freddy lives far away from all the restaurants he likes. Freddy is a capable frog, able to jump over a large number of cells. Unfortunately, on a given day, Freddy may be too hungry to jump very far. On a given day, he can only jump over at most d cells (note that he can also jump over fewer cells).
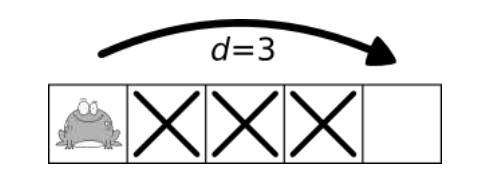
Another complication for Freddy is the path he jumps across is always under construction. Some of the cells are blocked off! Freddy doesn’t want to land in a cell under construction but is allowed to jump over them.
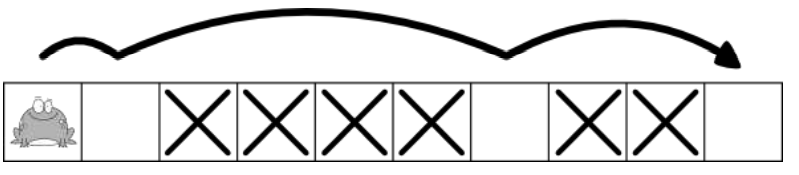
Freddy starts off in the first cell and must travel to the last cell where his destination restaurant resides. He would like to know if he can reach the last cell and how quickly he can reach it. Freddy always jumps towards his destination.
Input
The first input line contains two integers, c (2 ≤ c ≤ 50) and d (0 ≤ d ≤ 50), representing (respectively) the number of cells in the path from Freddy’s home to the restaurant (including his home and the restaurant) and the maximum number of cells Freddy can jump over in a single jump on that day. The second input line is a string consisting of c characters containing only ‘.’ 2 and ‘X’ characters where ‘.’ represents that the cell is okay for Freddy to occupy and ‘X’ represents that the cell is blocked by construction. The first and last characters of the string represent Freddy’s home and the restaurant, respectively; these two locations will never be blocked.
Output
Print the minimum number of jumps it takes Freddy to reach the restaurant. If it is not possible to reach the restaurant, print the number 0 instead.
Sample Input 1
8 3
.XX.X.X.
Sample Output 1
2
Sample Input 2
3 50
...
Sample Output 2
1
Sample Input 3
8 1
...XX...
Sample Output 3
0
Sample Input 4
10 4
..XXXX.XX.
Sample Output 4
3
题解
- 线性DP(O(n))
#include<bits/stdc++.h>
using namespace std;
int dp[55];
int main()
{
int n,m;//c,d
string str;
cin>>n>>m>>str; //输入:总长n,每次最多跳m步长,含障碍的地图str
int right=0; //当前可以达到的最右端的点位
for(int i=1,ii=min(m+1,n-1);i<=ii;i++) //标记第一步可以达到的位置(之后所有已经可以达到的位置都是正整数)
if(str[i]=='.')
dp[right=i]=1;
for(int i=1;i<n;i++) //从已可以到达的位置遍历
{
if(dp[i]) //如果可以已经到达
{
for(int j=right+1,jj=min(n-1,i+m+1);j<=jj;j++) //看看能否更新还未到达的点(能到达的最右边的点之后的点)
if(str[j]=='.')
dp[right=j]=dp[i]+1; //可以到达未到达的点,更新该点,标记为最右到达的点
}
}
printf("%d\n",dp[n-1]); //输出最右点的步数,0表示不能到达
// for(int i=0;i<n;i++) //辅助观察各点的步数更新结果用
// cout<<i<<" : "<<dp[i]<<" - "<<str[i]<<endl;
return 0;
}
D. Fujiyama Thursday
Description
During the past year, the UCF programming team members started a weekly dinner at Fujiyama Sushi. Usually, the programming team members wait for everyone to arrive to start eating, but as a wise programming team coach from the north of campus always says: “regionals is coming.” Heeding this ominous warning, the programming team members need to spend more time to prepare. To spend more time practicing, the programming team members will start eating as they arrive. However, they will still wait until everyone is done eating to leave Fujiyama. Each car the team members are taking holds exactly four people. As each car may take a different amount of time to arrive at Fujiyama and each team member may have different eating speeds, it is important to assign team members to cars in a careful manner. Any team member can be assigned to any car as all team members can drive any of the cars.
Given the time it takes for cars to arrive and eating speeds of the team members, determine the minimum amount of time needed for all the team members to finish eating if the team members are assigned to cars optimally.
Input
The first input line for the trip contains a single integer, c (1 ≤ c ≤ 50), representing the number of cars going to Fujiyama. The second input line contains c integers, di (1 ≤ di ≤ 45), representing the time (in minutes) it takes for the i-th car to arrive to Fujiyama. The third input line contains 4*c integers, t-j (1 ≤ t-j ≤ 75), representing the time (in minutes) it takes for the j-th-team member to finish eating.
Output
Print a single integer representing the minimum amount of time (in minutes) for all the team members to finish eating.
Sample Input 1
1
40
1 2 3 4
Sample Output 1
44
Sample Input 2
2
10 20
5 6 3 4 8 9 1 2
Sample Output 2
24
Sample Input 3
3
15 20 20
10 10 10 10 20 20 20 20 30 30 30 30
Sample Output 3
45
题解
- 贪心:吃得慢的人先走
#include<bits/stdc++.h>
using namespace std;
int input() //输入优化
{
char ch;
while((ch=getchar())<'0'||ch>'9');
int ret=ch-'0';
while((ch=getchar())>='0'&&ch<='9')
ret=(ret<<1)+(ret<<3)+ch-'0';
return ret;
}
int main()
{
int n;//原题的c
vector<int>cars_arrival,people_eating;//原题的d[],t[]
cin>>n;
for(int i=0;i<n;i++)
cars_arrival.push_back(input());
for(int i=0,ii=n*4;i<ii;i++)
people_eating.push_back(input());
sort(cars_arrival.begin(),cars_arrival.end());
sort(people_eating.begin(),people_eating.end());
reverse(people_eating.begin(),people_eating.end());
int anss=0;
for(int i=0;i<n;i++)
anss=max(anss,cars_arrival[i]+people_eating[i*4]);
cout<<anss<<endl;
return 0;
}
E. Chain Email
Description
A chain email is an email that people receive and then forward to all of their friends. This sort of email is very common amongst elderly people, who have notably bad memories. Elderly people’s memories are so bad that if they ever receive a chain email they will forward it to all of their contacts. This can become very problematic when elderly people continually send the same email to each other. For instance, if two people have each other in their contacts and if either of them receive a chain email they will continually send the email to each other back and forth forever. Email companies are worried that this will result in a massive amount of storage loss on their servers and have asked you to determine if a specific person were to start a chain email, who would receive that email forever.
Given each elderly person’s contacts and which elderly person will be starting a chain email, determine who will be indefinitely receiving emails.
Input
The first line of input will have two single-space-separated integers, p (1 ≤ p ≤ 50), indicating the number of people who use the email service and, s (1 ≤ s ≤ p), indicating the source of the chain email, where each person is labeled from 1 to p. Following this will be a single line with the names of all of the people, from person 1 to person p, who use the email service, each separated by exactly one space. All names will contain alphabetic characters only and be between 1 and 19 characters (inclusive) in length. Following this will be p lines. The i-th line will describe the contact list of the i-th person. This description will consist of an integer, m (0 ≤ m < p), indicating the number of contacts this person has, followed by the 1-based index of each of the contacts, each separated by exactly one space. It’s guaranteed that no one will contain themselves as a contact.
Output
Print the names of all of the people who will infinitely receive chain emails, assuming that everyone continually forwards the email to all of their contacts. Each name should be followed by a space. List these contacts in the order that they appear in the input. If no one will infinitely receive chain emails, then print “Safe chain email!” instead
Sample Input 1
3 1
James Sarah John
2 2 3
2 1 3
2 1 2
Sample Output 1
James Sarah John
Sample Input 2
3 1
James Sarah John
2 2 3
0
0
Sample Output 2
Safe chain email!
Sample Input 3
6 3
Ali Matt Glenn Sumon Arup Chris
2 3 5
0
1 4
1 1
1 2
2 5 4
Sample Output 3
Ali Matt Glenn Sumon Arup
题解
- 小图论题,从一个点进入,DFS搜索,找路径中是否存在强连通分量,以及其分支
#include<bits/stdc++.h>
using namespace std;
int input() //输入优化
{
char ch;
while((ch=getchar())<'0'||ch>'9');
int ret=ch-'0';
while((ch=getchar())>='0'&&ch<='9')
ret=(ret<<1)+(ret<<3)+ch-'0';
return ret;
}
vector<string>name; //各点的用户名字
vector<vector<int>>to; //可以到达的点编号
vector<int>chain; //当前搜索的链
vector<bool>inchain; //点是否在链上
vector<bool>forever,dforever; //是否会永远接受到信息、是否需要更新
void goo(int f)
{
// printf("goo ( %d )\n",f);
if(dforever[f]) //更新完成
return;
if(forever[f]) //会永远接收信息,需要更新
{
dforever[f]=true; //标记为不需要再更新
for(int i=0;i<(int)to[f].size();i++) //把他能扩散的点更新为会永远接收到信息
{
forever[to[f][i]]=true;
goo(to[f][i]);
}
return;
}
chain.push_back(f); //进入当前链
inchain[f]=true; //进入当前链
for(int i=0;i<(int)to[f].size();i++) //遍历可到达的点
{
if(inchain[to[f][i]]) //如果和先前链上的点成环
{
for(int j=chain.size()-1;chain[j]!=to[f][i];j--) //这两点和中间的点都构成环,即会永远接收信息
{
//需要标记and更新
forever[chain[j]]=true;
goo(chain[j]);
}
forever[to[f][i]]=true;
goo(to[f][i]);
break;
}
goo(to[f][i]); //如果不会成环,则继续DFS搜索图
}
chain.pop_back(); //退出当前链
inchain[f]=false; //退出当前链
return;
}
int main()
{
int n,s;
cin>>n>>s;
s--; //下标从0开始
name.resize(n);
inchain.resize(n,false);
forever.resize(n,false);
dforever.resize(n,false);
for(int i=0;i<n;i++)
cin>>name[i];
to.resize(n);
for(int i=0,j,jj;i<n;i++)
{
to[i].resize(jj=input());
for(j=0;j<jj;j++)
to[i][j]=input()-1; //下标从0开始
} //上面是初始化以及输入处理
goo(s); //从进入s点,发起信息,开始DFS
bool empty=true; //先标记无可怜的老人
for(int i=0;i<n;i++) //查找可怜的老人
{
if(forever[i]) //找到了
{
cout<<name[i]<<' '; //就输出
empty=false; //然后标记找到了
}
}
if(empty) //没找到
puts("Safe chain email!"); //输出安全结果
return 0;
}
F. Faster Microwaving
Description
Chris likes getting his food quickly so he cooks a lot using the microwave. However, he is frustrated by how microwave makers seem not to communicate well with makers of microwavable foods. For example, many microwaves have a “popcorn” button, but most microwave popcorn instructions say “Do not use the ‘popcorn’ button.” To avoid any chance of ruining his food, Chris uses only timed cooking, entering the time to cook each item in minutes and seconds (in MM:SS format) on the numbered buttons of the microwave. Since there is one digit per button, he has to press one digit at a time and move his finger between different digits, which is tedious and annoying because he’s hungry. One nice thing is that there is no button for the “:” as the microwave always interprets the last 2 digits as seconds, and inserts the “:” appropriately—however, it does not enforce a restriction that the last two digits are 59 seconds or less; if Chris presses 1, then 9, then 0 for a time of “1:90” it will cook for 1 minute and 90 seconds, which is the same as 2 minutes and 30 seconds. Chris would like to be able to enter the cooking times more quickly. He notices that it takes 1 “moment” (a unit of time just under half a second) to press each digit’s button firmly, and it also takes 1 moment (the same unit of time) to move his finger away from one digit’s button to find the button for a different digit. Therefore, to enter a time “4:00” takes 4 moments in total—one to press “4”, one to move from “4” to “0”, one to press “0”, and one to press “0” again immediately, without having to find the button. It also takes 4 moments to enter “4:45” (press 4, then 4 again, then move from 4 to 5, then press 5), but it takes 5 moments to enter “4:30” (4, then move, then 3, then move, then 0). After some experimentation, Chris devises the following plan to enter faster cooking times that are reasonably close to the recommended times in the cooking instructions for each item: 1. Based on the microwavable item type, consider using a range of proposed cooking times that are each within a small percent above or below the recommended cooking time. For example, using 10% with a recommended cooking time of 2 minutes and 30 seconds (2:30), the proposed cooking times would be the range of times from 2:15 to 2:45 inclusive. 2. Find the sequence of digits (buttons) that takes the lowest total moments to enter out of any of the proposed cooking times in the range. 3. If there are multiple sequences of digits that have the same lowest total moments, choose the sequence that yields an actual cooking time that is closest to the recommended cooking time. Chris has verified that the above plan always results in a unique answer so you may assume so.
Given the recommended cooking time for a microwavable item, and a percent to use for the range of proposed cooking times, output the sequence of digits that Chris should press in order to start the microwave as fast as possible, according to his plan.
Input
The first input line contains only the recommended cooking time for the microwavable item, which consists of exactly 5 characters in the format MM:SS with 2-digit minutes MM(00 ≤ MM ≤ 20) and 2-digit seconds SS (SS ∈ {00, 15, 30, 45}). The recommended cooking time will be at least 00:15 (15 seconds). The second input line contains only an integer p (2 ≤ p ≤ 10), which is the percent of the recommended cooking time that defines the range of lower and higher proposed cooking times.
Output
Print the exact digits that should be pressed, in the order they should be pressed.
Note that the seconds are always integers and the time must be “within” the percent range. For example, for a recommended cooking time of 00:45 and 10%, the range of proposed cooking times is 41 seconds to 49 seconds (45 ± 4, because 40 and 50 are not within 10% of the recommended time).
Sample Input 1
01:30
4
Sample Output 1
88
Sample Input 2
00:30
10
Sample Output 2
33
Sample Input 3
06:00
8
Sample Output 3
555
题解
- 看数据范围,不用考虑巧解,枚举就行
#include<bits/stdc++.h>
using namespace std;
int op(int v) //计算按键方式操作数
{
int now,las=v%10,ret=0;
while(v)
{
now=v%10;
if(now==las)
ret++;
else
{
las=now;
ret+=2;
}
v/=10;
}
return ret;
}
int trans_time(int v) //把按键方式转化成时间(s)
{
v=v%100+v/100*60;
return v;
}
int main()
{
int m,s,p; //对应输入
scanf("%2d:%2d\n%d",&m,&s,&p);
int all_s=m*60+s; //计算需要时间(s)
int min_s=max(0,all_s-all_s*p/100); //计算最小设置时间
int max_s=all_s+all_s*p/100; //计算最大设置时间
// int min_m=max(0,(min_s-99)/60); //最小可能分钟
int max_m=max_s/60+1; //最大可能分钟
int max_press=max_m*100+max_s%100; //最大按键操作结果
int anss=-1; //按键答案
int min_op=101; //当前最小操作数
int anss_s; //当前答案对应时间(s)
int tmp_s; //当前对应时间(s)
int tmp_op; //当前操作数
for(int i=0;i<=max_press;i++) //从0开始遍历按键操作结果
{
tmp_s=trans_time(i); //计算转化时间
if(tmp_s>=min_s&&tmp_s<=max_s) //可行
{
if((tmp_op=op(i))<min_op) //查看操作数是否更简
{
anss=i; //更新答案
anss_s=tmp_s;
min_op=tmp_op;
}
else if(tmp_op==min_op) //查看操作数是否一样简
{
if(abs(tmp_s-all_s)<abs(anss_s-all_s)) //查看偏移时间是否更少
{
anss=i; //更新答案
anss_s=tmp_s;
min_op=tmp_op;
}
}
}
}
cout<<anss<<endl; //输出答案
return 0;
}