【学习笔记VoxelMorph系列文章2】：《Unsupervised Learning for Fast Probabilistic Diffeomorphic Registration》

传统的可变形配准需要大量的计算时间，基于学习的配准方法可以减少训练时间但是需要标签值（比较少）或者没有保证微分同胚特性。本文提出一个概率生成模型并推导一个基于无监督学习的推理算法，不仅保证了微分同胚特性，还提供了不确定估计。

1.简介

可变形配准计算出两幅图像间的密集对应关系，是许多医疗图像分析任务的基础。传统的方法解决空间形变的优化问题，例如：弹性模型、B样条、密集矢量场和离散方法（discrete methods）。将变形限制为微分同胚会保留某些理想的特性，已经有比较成熟的方法实现微分同胚（LDDMM，DARTEL，SyN等），但是这些方法需要大量时间与资源来运行。有些方法训练神经网络将输入图像对映射输出一个变形场，这通常需要标准图像（从更传统的配准方法获取），由此引入偏差，所以需要更合理的预处理方法。此前的一些文章探索空间形变网络的无监督变换策略仅仅在仿射变换和小位移场上，并且只在3D补丁和2D切片上进行验证。
本文提出了一个配准公式推导概率生成模型的变分形式。使用的是带有直接代价函数的卷积神经网络，并且使用微分同胚层与变换层实现了端到端的微分同胚配准。可以实现较为理想的配准，同时保持微分特性，减少了运行时间并且估计了配准的不确定性。

1.1微分同胚配准

微分同胚变换时可微和可逆的，因此保持了拓扑特性。形变场定义为常微分方程：$$\frac{\partial {\varphi }^{(t)}}{\partial t}=v({\varphi }^{(t)})$$，其中${\varphi }^{(0)}=Id$ 是恒等变换（ODE），t 是时间，对静止速度场 $v$在 t = [0, 1] 上积分获得最终配准场${\varphi }^{(t)}$ 。使用缩放和平方计算积分，平稳的ODE表示微分同胚的单参数子集，在群论中，$v$是李代数的一员，求幂得到 ${\varphi }^{(1)}$， ${\varphi }^{(1)}$是李群：${\varphi }^{(1)}=e^v$，（李代数是李群的正切空间） 由子单参数子空间的性质可知，对于标量$t$和$t^{\prime }$，$e^{(t+t^{\prime })v}=e^{tv}\circ e^{t^{\prime }v}$，其中$\circ$表示与李群相关的组成图（composition map ）。${\varphi }^{(1/2^T)}=p+v(p)$，其中$p$是空间位置图，循环计算${\varphi }^{(1/2^{t-1})}={\varphi }^{(1/2^t)}\circ {\varphi }^{(1/2^t)}$可以求得${\varphi }^1={\varphi }^{(1/2)}\circ {\varphi }^{(1/2)}$，选择合适的T可以使$v\approx 0$。

2.方法

提出了一种变分推理方法，使用卷积神经网络、微分同胚积分和空间变换层实现。在实现微分同胚的同时提供了不确定性估计。

2.1生成模型

假设$x$，$y$分别表示两幅MRI图像，$z$表示变换函数的隐变量，关于$z$的先验概率是：$$p(z)=\mathcal{N}(z;0,{\Sigma }_z)$$其中，$\mathcal{N}(\cdot ;\mu ,\Sigma )$服从多元正态分布且$\sim (\mu ，\Sigma )$，$z$有很宽泛的表示范围，既可以表示密集位移场的低维嵌入，也可以表示位移场本身。在此，$z$代表静态速度场，它通过ODE指定一个微分同胚映射，取$L=D-A$表示在体素网格上定义的邻域图的拉普拉斯算子，其中$D$表示图的度矩阵（度矩阵是对角阵，对角上的元素为各个顶点的度。）
$A$表示体素相邻矩阵。使用${\Sigma }_z^{-1}={\Lambda }_z=\lambda L$,对$z$进行空间平滑，其中${\Lambda }_z$是精密矩阵$\lambda$控制速度场$z$的尺度。
让$x$是扭曲图像 $y$的噪声观测:$$p(x|z;y)=\mathcal{N}(x;y\circ {\varphi }_z,{\sigma }^2Ⅱ)$$
其中，${\sigma }^2$表示图像加性噪声的方差。
目标是估计后验配准概率$p(z|x；y)$，通过MAP估计（最大后验概率）获得新图像对$(x,y)$的最可能的配准场${\varphi }_z$，以及配准的不确定性估计。

2.2学习

使用变分方法，引入近似后验概率$q_{\psi }(z|x；y)$，使用$\psi$进行参数化，通过最小化KL散度（变分下界的相反数，相对熵）
$$\begin{gathered} mi{n}_{\psi }KL[q_{\psi }(z|x;y||p(z|x;y))] \\ =mi{n}_{\psi }{\mathbf{E}}_q[\log q_{\psi }(z|x;y)-\log p(z|x;y)] \\ =mi{n}_{\psi }{\mathbf{E}}_q[\log q_{\psi }(z|x;y)-\log p(z,x,y)]+\log p(x;y) \\ =mi{n}_{\psi }KL[q_{\psi }(z|x;y)||p(z)-{\mathbf{E}}_q[\log p(x|z;y)] \end{gathered}$$

$($可能是水平原因我没看懂这个公式的第三步，下面我描述一下我的理解，后验概率公式：$p(x)p(\omega |x)=p(\omega )p(x|\omega )$，其中$p(x)$是已知的全概率，$p(\omega )$是先验概率，$p(\omega |x)$为后验概率，$p(x|\omega )$为类概率密度（顾名思义，就是某一类的概率），带入本公式得：$p(z|x;y)=\frac{p(z)p(x|z;y)}{p(x)}，y$为浮动图像，$x$为固定图像，所以$p(x)$已知为常数省略了。所以我修改上式如下：
m i n ψ K L [ q ψ ( z ∣ x ; y ∣ ∣ p ( z ∣ x ; y ) ) ] = m i n ψ E q [ log ⁡ q ψ ( z ∣ x ; y ) − log ⁡ p ( z ∣ x ; y ) ] = m i n ψ E q { log ⁡ q ψ ( z ∣ x ; y ) − log ⁡ [ p ( z ) p ( x ∣ z ; y ) ] } = m i n ψ E q [ log ⁡ q ψ ( z ∣ x ; y ) − log ⁡ p ( z ) − log ⁡ p ( x ∣ z ; y ) ] = m i n ψ E q [ log ⁡ q ψ ( z ∣ x ; y ) − log ⁡ p ( z ) ] − m i n ψ E q [ log ⁡ p ( x ∣ z ; y ) ] = m i n ψ K L [ q ψ ( z ∣ x ; y ) ∣ ∣ p ( z ) − E q [ log ⁡ p ( x ∣ z ; y ) ] min_{\psi}KL[q_{\psi}(\mathcal{z|x;y||p(z|x;y)})]\\ =min_{\psi}\mathbf{E}_{q}[\log\mathcal{q_{\psi}(z|x;y)}-\log\mathcal{p(z|x;y)}]\\ =min_{\psi}\mathbf{E}_{q}\{\log\mathcal{q_{\psi}(z|x;y)}-\log\mathcal{[p(z)p(x|z;y)]}\} \\ =min_{\psi}\mathbf{E}_{q}[\log\mathcal{q_{\psi}(z|x;y)}-\log\mathcal{p(z)}-\log\mathcal{p(x|z;y)}] \\ =min_{\psi}\mathbf{E}_{q}[\log\mathcal{q_{\psi}(z|x;y)}-\log\mathcal{p(z)}]-min_{\psi}\mathbf{E}_{q}[\log\mathcal{p(x|z;y)}]\\ =min_{\psi}KL[\mathcal{q_{\psi}(z|x;y)||p(z)}-\mathbf{E}_{q}[\log\mathcal{p(x|z;y)}] minψ​KL[qψ​(z∣x;y∣∣p(z∣x;y))]=minψ​Eq​[logqψ​(z∣x;y)−logp(z∣x;y)]=minψ​Eq​{ logqψ​(z∣x;y)−log[p(z)p(x∣z;y)]}=minψ​Eq​[logqψ​(z∣x;y)−logp(z)−logp(x∣z;y)]=minψ​Eq​[logqψ​(z∣x;y)−logp(z)]−minψ​Eq​[logp(x∣z;y)]=minψ​KL[qψ​(z∣x;y)∣∣p(z)−Eq​[logp(x∣z;y)]

由$\mathbf{K}\mathbf{L}$散度公式我认为${\mathbf{E}}_q$应该写成$\sum q(z|x;y)$，但是上述公式也并未修改 $)$

将后验建模为多元正态，$q_{\psi }(z|x;y)=\mathcal{N}(z;{\mu }_{z|x,y},{\Sigma }_{z|x,y})$，其中${\Sigma }_{z|x,y}$是对角矩阵。
使用参数为$\psi$的卷积神经网络$de{f}_{\psi (x,y)}$来估计${\mu }_{z|x;y}$和${\Sigma }_{z|x;y}$，使用随机梯度法优化变分下界，来学习参数$\psi$。
对于输入图像对$(x,y)$和样例$z_k\sim q_{\psi }(z|x;y)$，可以用以下损失函数计算$y\circ {\varphi }_{zk}$：
$$\begin{gathered} \mathcal{L}(\psi ,x,y)=-{\mathbf{E}}_q[\log p(x|z;y)]+KL[q_{\psi }(z|x;y)||p(z)] \\ =\frac{1}{2{\delta }^{2}K}\sum _k||x-y\circ {\varphi }_{zk}|{|}^2+\frac{1}{2}[tr(\lambda D{\Sigma }_{z|x;y}-\log |{\Sigma }_{z|x;y}|)+{\mu }_{z|x;y}^T{\Lambda }_z{\mu }_{z|x;y}]+const \end{gathered}$$
其中，分母上的K表示使用样本的数目，本实验只有一个样本（固定图像？）K=1，第一个平方项表示希望扭曲图像与$x$相似；第二项表示希望后验概率尽可能的接近先验概率$p(z)$，变分协方差$\log {\Sigma }_{z|x;y}$为对角阵；第三项为空间平滑均值${\mu }_{z|x;y}^T{\Lambda }_z{\mu }_{z|x;y}=\frac{\lambda }{2}\sum {\sum }_{j\in N(I)}(\mu [i]-\mu [j]{)}^2,N(I)$表示体素$i$的邻域体素；最后一项是常量，将${\delta }^2$与$\lambda$设置为固定超参数(待训练)。

2.3神经网络框架

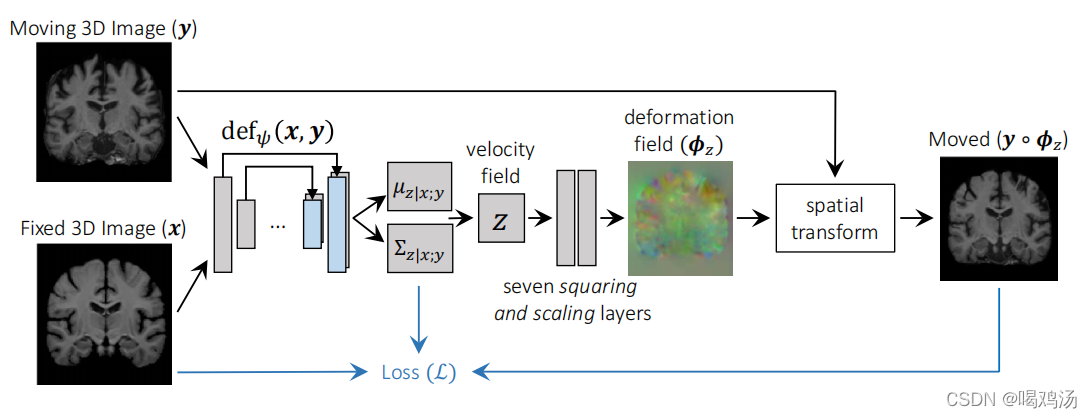
设计了3D-Uet类型的网络框架（如上图），输入$(x,y)$输出${\mu }_{z|x;y}$(期望)和${\Sigma }_{z|x;y}$（方差）。由四层U-Net构成，(具体结构可见)每层卷积层（3×3的卷积核）后加入LeakyReLu激活函数。
为了实现无监督的$\mathcal{L}(\psi ,x,y)$，必须保证形成$y\circ {\varphi }_z$，使用了一个通过重参数化技巧来采样一个新的$z_k\sim \mathcal{N}({\mu }_{z|x;y},{\Sigma }_{z|x;y})$。
本文提出了一个新的缩放和平方(缩小和扩张UNet的特点)的网络层计算空间变化${\varphi }_{zk}=e^{z_k}$。给定两个三维矢量场$(a,b)$，对每个体素p，使用线性插值法计算$(a\circ b)(p)=a(b(p))$，$a$中非整数体素的坐标$b(p)$。（这里有没有懂的，在评论区交流一下）
首先$v^{(1/2^T)}=z_k$，递归的使用网络层计算${\varphi }^{(1/2^{t-1})}={\varphi }^{(1/2^t)}\circ {\varphi }^{(1/2^t)}$(原文这里是+，但对比上文我觉得是-)，最后得出$v^{(1)}\triangleq {\varphi }_{z_k}=e^{z_k}$，使用T=7，输入图像尺寸为128（$2^7$），最后通过空间变换层使用计算得到的微分同胚形变场${\varphi }_{z_k}$扭曲浮动图像。最后会得到三个输出${\mu }_{z|x;y},{\Sigma }_{z|x;y},y\circ {\varphi }_{z_k}$。

本框架的每一步都是可微的，使用随机梯度下降的方法计算网络参数。

2.4配准和不确定性

目的是使用学习到的参数，使$(x,y)$两个输入接近。
首先通过在两个输入图像上评估神经网络 $de{f}_{\psi }(x,y)$，使用下式获得${\hat{z}}_k$,$${\hat{z}}_k=argma{x}_{z_k}p(z_k|x;y)={\mu }_{z|x:y}$$
然后使用缩放和平方网络计算${\varphi }_{{\hat{z}}_k}$。同时获得${\Sigma }_{z|x;y}$估计每个体素j上的速度场z的不确定性：$$H(z[j])\approx \mathbf{E}[-\log q_{\psi }(z|x;y)]=\frac{1}{2}\log 2\pi {\Sigma }_{z|x;y}[j,j]$$
同时还估计形变场${\varphi }_z$的不确定性，采样一些代表$z_{k^{\prime }}\sim q_{\psi }(z|x;y)$，经微分同胚层传播计算${\varphi }_{z_{k^{\prime }}}$，计算样本间的对角协方差${\hat{\Sigma }}_{{\varphi }_z}[j,j]$，所以不确定性为：
$$H(\varphi [j])\approx \frac{1}{2}\log 2\pi {\hat{\Sigma }}_{{\varphi }_z}[j,j]$$

实验

本实验在基于3D地图（atlas，所有数据的平均值）上进行配准，使用一个由额外数据集计算的地图。

数据预处理

使用了大尺度、多范围的T1加权脑部MRI图像（来自八个公开数据集，攻击7829张图像，ADNI，OASIS，ABIDE，ADHD200，MCIC，PPMI，HABS和Harvard GSP），所有图像重采样为具有1mm各项同性的体素，进行仿射空间归一化并且使用FreeSurfer去除颅骨，提取脑部图像。裁剪图像为（$160\times 192\times 224$），使用29个解剖结构，按7329：250：250划分数据集。

评价指标

对每个解剖结构进行DICE系数评估，同时还评价微分同胚的性能。雅可比行列式$J_{\varphi }(p)=▽\varphi (p)\in {\mathcal{R}}^{3\times 3}$（点我直达）可以评估行变场在体素p周围的局部属性。$J_{\varphi }(p)>0$的体素是微分同胚的（既可逆又保持方向），统计$J_{\varphi }(p)\le 0$的体素。

结果分析

对比ANTs（一个软件包）与对称归一化（Symmetric Normalization，SyN），结果如下：

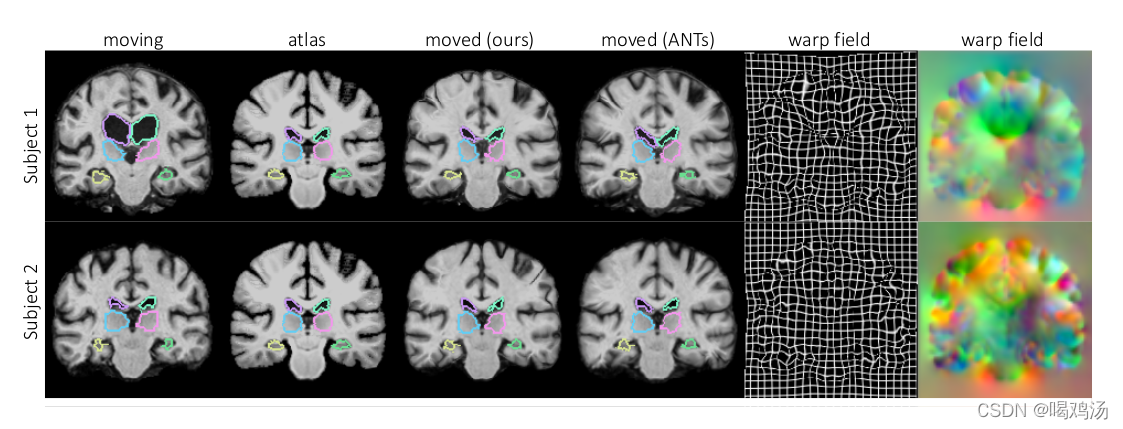
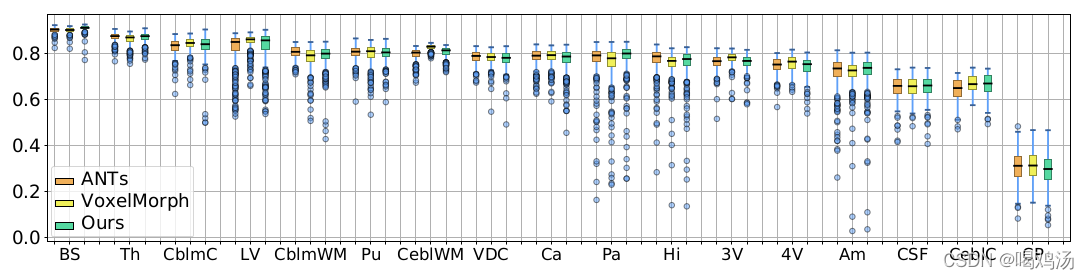
实例图如上，配准结果与ANTs几乎一样，且行变场并没有紊乱（有时会为了配准而配准，即出现大幅跳跃，不连续现象）视觉上看不出有跳跃的地方。表格中的数据更加直观表明效果好，计算时间短，具有可确定性，良好的微分同胚特性（负雅可比体素的数目非常少）。

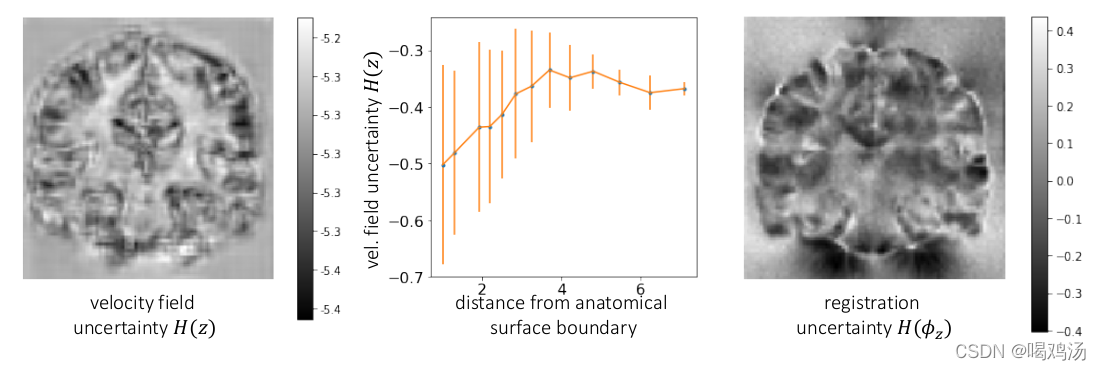
上图是图像的不确定性估计，左图为行变场的不确定性，边界的不确定性较小，右图为扭曲后的图像，均匀扫描的地方（eg:白质）不确定性较高。中间折线图没看懂。

参数设置

经实验，发现设置${\sigma }^2\sim (0.035{)}^2,\lambda =70000$时效果理想。

结论

提出一种使用微分图像配准的概率模型，推导出使用CNN和直观损失函数的学习算法，还引入了缩放和平方层。实现了快速有效的运算，还保证了微分同胚，提供不确定性估计。