[Optimierung] Optimierung des städtischen Verkehrssignals basierend auf dem verbesserten genetischen Algorithmus GA von matalb [Matlab-Quellcode einschließen 214]

1. Einleitung

1 Die grundlegende Theorie des genetischen Algorithmus Die
Genetik glaubt, dass Vererbung ein in jeder Zelle eingekapselter und in Form von Genen im Chromosom enthaltener genetischer Anweisungscode ist. Jedes Gen hat eine spezielle Position und kontrolliert eine spezielle Eigenschaft. Das von jedem Gen produzierte Individuum hat einen gewissen Grad an Anpassungsfähigkeit an die Umwelt. Genhybridisierung und -mutation können Nachkommen hervorbringen, die an die Umwelt angepasst werden können. Durch natürliche Selektion des Überlebens der Stärksten bleibt die Genstruktur mit hohem Fitnesswert erhalten.
Der genetische Algorithmus stützt sich auf die genetische Theorie des "Überlebens der Stärksten" und drückt die Lösung des Optimierungsproblems als "Überleben der Stärksten" von "Chromosomen" aus. Durch die Entwicklung von Generationen der Vervielfältigung, Überkreuzung und Mutation von Die "Chromosomen" -Gruppe erhalten wir endlich. Es ist das Individuum, das am besten an die Umgebung angepasst werden kann, um die optimale oder zufriedenstellende Lösung für das Problem zu erhalten. Dies ist ein sehr paralleler, zufälliger und adaptiver allgemeiner Optimierungsalgorithmus.
Eine Reihe von Vorteilen des genetischen Algorithmus hat ihn in den letzten Jahren immer wichtiger gemacht, und er wurde in vielen Bereichen zur Lösung von Optimierungsproblemen eingesetzt, einschließlich seiner erfolgreichen Anwendung im Transportbereich.
2 Eigenschaften des
genetischen Algorithmus Der genetische Algorithmus ist ein selbstadaptiver probabilistischer Suchalgorithmus zur globalen Optimierung, der durch Simulation des genetischen und evolutionären Prozesses in der biologischen natürlichen Umgebung gebildet wird. Es ist eine Art robuster Suchalgorithmus, der bei der Optimierungsberechnung komplexer Systeme verwendet werden kann. Im Vergleich zu anderen Optimierungsalgorithmen weist er viele Eigenschaften auf.
Es gibt drei traditionelle Hauptoptimierungsalgorithmen: Aufzählungs-, Heuristik- und Suchalgorithmen:
1. Aufzählungsmethode Die
Aufzählungsmethode listet alle möglichen Lösungen im Satz der realisierbaren Lösungen auf, um die exakt optimale Lösung zu finden. Für kontinuierliche Funktionen erfordert dieses Verfahren zuerst eine Diskretisierung, so dass aufgrund der diskreten Verarbeitung möglicherweise nie die optimale Lösung erreicht wird. Wenn der Aufzählungsraum relativ groß ist, ist die Lösungseffizienz dieses Algorithmus außerdem sehr gering und äußerst zeitaufwendig.
2. Heuristischer Algorithmus Der
heuristische Algorithmus sucht nach einer heuristischen Regel, die eine praktikable Lösung ergeben kann, um eine optimale Lösung oder eine ungefähre optimale Lösung zu finden. Die Effizienz des heuristischen Algorithmus ist relativ hoch, aber für jedes Problem, das gelöst werden muss, muss seine eindeutige heuristische Regel gefunden werden. Diese heuristische Regel ist im Allgemeinen nicht universell und für andere Probleme nicht geeignet.
3. Suchalgorithmus
Der Suchalgorithmus führt eine Suchoperation in einer Teilmenge des realisierbaren Lösungssatzes durch, um die optimale Lösung oder die ungefähre optimale Lösung des Problems zu finden. Obwohl der Suchalgorithmus nicht garantieren kann, dass die optimale Lösung für das Problem erhalten wird, kann bei ordnungsgemäßer Verwendung einiger heuristischer Kenntnisse ein gutes Gleichgewicht zwischen der Qualität und der Effizienz der ungefähren Lösung erreicht werden.
3 Der Workflow des grundlegenden genetischen Algorithmus
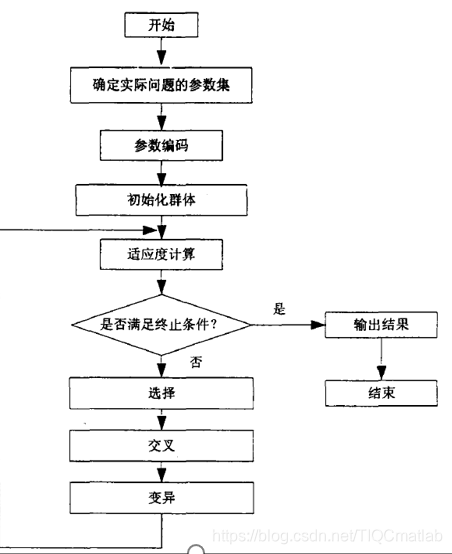
Fügen Sie hier eine Bildbeschreibung ein
4 Fitnessfunktion

5 Auswahloperator
Auswahl, auch als Replikation bezeichnet, ist der Prozess der Auswahl von Personen mit starker Vitalität in einer Gruppe, um eine neue Gruppe zu generieren. Der genetische Algorithmus verwendet Selektionsoperatoren, um das Überleben der Stärksten bei Individuen in der Gruppe durchzuführen, und wählt entsprechend der Fitness jedes Individuums aus. Individuen mit höherer Fitness werden eher in die Population der nächsten Generation vererbt, und umgekehrt. Auf diese Weise kann der Fitnesswert der Personen in der Gruppe kontinuierlich an die optimale Lösung herangeführt werden. Die Bestimmung des Auswahloperators wirkt sich direkt auf die Berechnungsergebnisse des genetischen Algorithmus aus.
Hier sind einige typische und häufig verwendete Auswahloperatoren:
1. Roulette-Auswahl
2. Zufällige Auswahl des Wettbewerbs
3. Zufällige Traversalauswahl
4. Sortierauswahl
5. Liga-Auswahl
6 Crossover-Operatoren
Im Folgenden werden mehrere Crossover-Operatoren vorgestellt, die für binär codierte Personen oder dezimal codierte Personen geeignet sind.
l.
Einzelpunkt- Überkreuzung Einzelpunkt-Überkreuzung (Einpunkt-Überkreuzung), auch als einfache Überkreuzung bezeichnet, ist die häufigste grundlegende Kreuzungsoperator. Es beginnt mit einem zufälligen Auswahlpunkt in einer binären Zeichenfolge. Für jedes Paar von Individuen, die miteinander gepaart sind, tauschen sie an ihren Kreuzungspunkten Teilchromosomen der beiden Individuen gemäß der festgelegten Kreuzungswahrscheinlichkeit aus, wodurch zwei neue Individuen erzeugt werden.
2.
Zweipunkt- Überkreuzung und Mehrpunkt-Überkreuzung Unter Zweipunkt-Überkreuzung versteht man die Einstellung von zwei Überkreuzungspunkten in der einzelnen Codezeichenfolge und den anschließenden teilweisen Genaustausch. Der spezifische Prozess der Zweipunktkreuzung ist:
(1) Zwei Kreuzungspunkte werden sofort in den zwei einzelnen Codezeichenfolgen gesetzt, die miteinander gepaart sind.
(2) Tauschen Sie einen Teil der Chromosomen zweier Individuen zwischen den beiden festgelegten Schnittpunkten aus.
3. Uniform Crossover
Uniform Crossover bedeutet, dass die Gene an jedem Ort von zwei gepaarten Individuen mit der gleichen Crossover-Wahrscheinlichkeit ausgetauscht werden, um zwei neue Individuen zu bilden. Die spezifische Operation kann verwendet werden, um zu bestimmen, wie jedes Gen des neuen Individuums von welchem Eltern-Individuum bereitgestellt wird, indem eine Maske gesetzt wird.
4. Arithmetische Frequenzweiche Die
arithmetische Frequenzweiche bezieht sich auf die lineare Kombination zweier Individuen, um zwei neue Individuen zu erzeugen. Um lineare Kombinationsoperationen ausführen zu können, ist das Operationsobjekt der arithmetischen Schnittmenge im Allgemeinen die Person, die durch den Gleitkommazahlencode dargestellt wird.
7 Mutationsoperator Die
sogenannte Mutationsoperation im genetischen Algorithmus bezieht sich auf das Ersetzen des Genwerts eines Locus in der einzelnen Chromosomen-Codierungskette durch andere Allele des Locus, um ein neues Individuum zu bilden. Die Mutation ist eine der Hauptmethoden des genetischen Algorithmus zur Erzeugung neuer Individuen. Die Mutationsoperation kann die Vielfalt der Population während der Operation des Algorithmus aufrechterhalten, eine vorzeitige Reife wirksam vermeiden und die lokale Suchfähigkeit des genetischen Algorithmus verbessern.
Der Mutationsoperator im genetischen Algorithmus sollte auch gemäß verschiedenen Anforderungen ausgewählt und entworfen werden. Im Folgenden sind einige häufig verwendete Mutationsoperatoren aufgeführt.
8 Verbesserung des genetischen Algorithmus
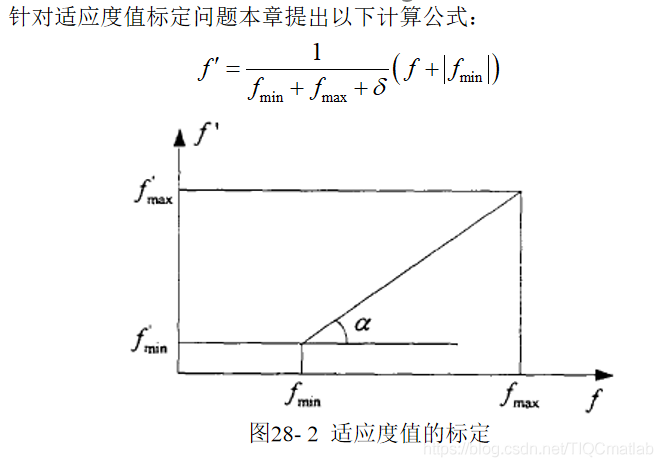
Fügen Sie hier eine Bildbeschreibung ein

Zweitens der Quellcode

%% GA
%% 清空环境变量
clc,clear,close all
warning off
% feature jit off
%% 遗传算法参数初始化
maxgen = 50;                      % 进化代数，即迭代次数
sizepop = 100;                     % 种群规模
pcross = [0.7];                    % 交叉概率选择，0和1之间
pmutation = [0.1];                 % 变异概率选择，0和1之间
%染色体设置
lenchrom=ones(1,3);    % t1、t2、t3
bound=[38,59;26,37;33,44;];   % 数据范围
%---------------------------种群初始化------------------------------------
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness = [];                      %每一代种群的平均适应度
bestfitness = [];                     %每一代种群的最佳适应度
bestchrom = [];                       %适应度最好的染色体

%% 初始化种群
for i=1:sizepop
    % 随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound); % 编码（binary和grey的编码结果为一个实数，float的编码结果为一个实数向量）
    x=individuals.chrom(i,:);
    % 计算适应度
    individuals.fitness(i)=fun(x);   % 染色体的适应度 
end

%% 找最好的染色体
[bestfitness bestindex] = min(individuals.fitness);
bestchrom = individuals.chrom(bestindex,:);    % 最好的染色体
% 记录每一代进化中最好的适应度和平均适应度
trace = [bestfitness]; 

%% 迭代求解最佳初始阀值和权值
% 进化开始
for i=1:maxgen
    disp(['迭代次数：  ',num2str(i)])
    % 选择
    individuals=Select(individuals,sizepop); 
    % 交叉
    individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);

    % 计算适应度
    for j=1:sizepop
        x=individuals.chrom(j,:);        % 解码
        individuals.fitness(j)=fun(x);   % 染色体的适应度 
    end
%% 改进的GA
%% 清空环境变量
% clc,
clear % ,close all % 清除变量空间
warning off      % 消除警告
% feature jit off  % 加速代码执行
%% 遗传算法参数初始化
maxgen = 50;                      % 进化代数，即迭代次数
sizepop = 100;                     % 种群规模
pcross = [0.7];                    % 交叉概率选择，0和1之间
pmutation = [0.01];                 % 变异概率选择，0和1之间
delta = 0.1;
% 城市交通信号系统参数
C = 140;
L = 10;
load('data.mat')  % 包含交通流量q以及饱和流量xij
q = q./3600;      % 转化为秒s
xij = xij./3600;  % 转化为秒s
%染色体设置
lenchrom=ones(1,3);    % t1、t2、t3
bound=[38,59;26,37;33,44;];   % 数据范围
%---------------------------种群初始化------------------------------------
individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness = [];                      %每一代种群的平均适应度
bestfitness = [];                     %每一代种群的最佳适应度
bestchrom = [];                       %适应度最好的染色体

%% 初始化种群
for i=1:sizepop
    % 随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound); % 编码（binary和grey的编码结果为一个实数，float的编码结果为一个实数向量）
    x=individuals.chrom(i,:);
    % 计算适应度
    individuals.fitness(i)=fun1(x);   % 染色体的适应度 
end

%% 找最好的染色体
[bestfitness bestindex] = min(individuals.fitness);
bestchrom = individuals.chrom(bestindex,:);    % 最好的染色体
% 记录每一代进化中最好的适应度和平均适应度
trace = [bestfitness]; 

%% 迭代求解最佳初始阀值和权值
% 进化开始
for i=1:maxgen
    disp(['迭代次数：  ',num2str(i)])
    % 选择
    individuals=Select1(individuals,sizepop); 
    % 交叉
    individuals.chrom=Cross1(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation1(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);

    % 计算适应度
    for j=1:sizepop
        x=individuals.chrom(j,:);        % 解码
        individuals.fitness(j)=fun1(x);   % 染色体的适应度 
    end
    fmax = max(individuals.fitness);     % 适应度最大值
    fmin = min(individuals.fitness);     % 适应度最小值
    favg = mean(individuals.fitness);  % 适应度平均值
    individuals.fitness = (individuals.fitness + abs(fmin))./(fmax+fmin+delta); %适应度标定
    
  
    [newbestfitness,newbestindex]=min(individuals.fitness);
    [worestfitness,worestindex]=max(individuals.fitness);
   
    if bestfitness>newbestfitness
        bestfitness=newbestfitness;
        bestchrom=individuals.chrom(newbestindex,:);
    end

Drei laufende Ergebnisse

Fügen Sie hier eine Bildbeschreibung ein

Viertens Bemerkungen