Autor: Yu Fan
Hintergrund
Wenn wir auf die Entwicklungsgeschichte der neuronalen Netzwerkarchitektur zurückblicken, können wir feststellen, dass Symmetrie immer eine verborgene und zentrale Rolle gespielt hat und geometrisches Deep Learning die Bedeutung der Symmetrie hervorhebt. Einerseits haben wir in den Bereichen traditionelles Computer Vision und Verarbeitung natürlicher Sprache gesehen, dass die auf Transformer basierende Netzwerkarchitektur in den letzten Jahren erstaunliche Ergebnisse erzielt hat. Andererseits spielt die Symmetrie als erstes Prinzip in der Naturwissenschaft eine wichtige Rolle. Daher haben wir Grund zu der Annahme, dass geometrisches Deep Learning aus symmetrischer Sicht eine wichtige Rolle bei der Kombination von künstlicher Intelligenz und Wissenschaft spielen wird.
Abbildung 1: Die Kombination von geometrischem Deep Learning in den Bereichen künstliche Intelligenz und Wissenschaft
Tatsächlich hat Deep Geometry Learning beeindruckende Ergebnisse im Bereich der KI für die Wissenschaft erzielt und wird eine immer wichtigere Rolle spielen. Alphafold2 basiert auf graphischen neuronalen Netzen und Transformer und zeigt eine sehr hohe Genauigkeit bei der Vorhersage von Proteinstrukturen. Bei der Vorhersage und Erzeugung kleiner Molekülstrukturen kann das Hinzufügen zusätzlicher Starrkörpertransformationssymmetrie (E(3)-Symmetriegruppe) im euklidischen Raum zum graphischen neuronalen Netzwerk die Berechnungsgenauigkeit erheblich verbessern und die Trainingskomplexität verringern. Da die Erdoberfläche eine zweidimensionale Kugel ist, beinhaltet die globale Wettervorhersage Probleme wie die Faltung auf der Mannigfaltigkeit und die Koordinatenspezifikationstransformation. Geometrisches Deep Learning bietet einen systematischen theoretischen Rahmen für den Entwurf neuronaler Netze. In der Kosmologie sind Raum und Zeit aufgrund der Schwerkraft gekrümmt, und geometrisches Deep Learning liefert eine theoretische Grundlage für die Kombination dieser gekrümmten Riemannschen Mannigfaltigkeitsstruktur und KI.
Andererseits ist der Grad der Integration mit KI in Grundlagenwissenschaften wie der Physik der kondensierten Materie und der Quantenphysik noch nicht tiefgreifend. Dies liegt daran, dass in diesen Bereichen das systematische theoretische Wissen des Menschen relativ gut entwickelt ist, es jedoch sehr schwierig ist, qualitativ hochwertige Daten zu erhalten. Daher ist es besonders wichtig , wie bekanntes Wissen in neuronale Netze „eingebracht“ und die Datennutzung verbessert werden kann .
Gruppenäquivariante neuronale Netze haben überraschende Vorteile bei der Verbesserung der Datennutzung gezeigt. Bei der Klassifizierungsaufgabe des dreidimensionalen Tetris gibt es beispielsweise insgesamt 8 Konfigurationen. Der traditionelle Ansatz erfordert eine große räumliche Rotation jeder Datenkonfiguration zur Datenverbesserung, was zweifellos die Datenmenge und die Komplexität des Trainings erheblich erhöht und seine Vorhersagegenauigkeit nicht garantieren kann. Im E(3)-äquivarianten neuronalen Netzwerk benötigt jede Konfiguration nur ein Datenelement oder sogar weniger, wenn die beiden Konfigurationen durch eine E(3)-Transformation verbunden werden können. Während die erforderliche Datenmenge erheblich reduziert wird , ist die Vorhersagegenauigkeit auf theoretischer Ebene gewährleistet. Gleichzeitig weist dieses neuronale Netzwerk eine bessere Interpretierbarkeit und Ausdrucksfähigkeit auf .
Unter allen bekannten Erkenntnissen ist die Symmetrie ein tiefgreifendes und grundlegendes Wissen und auch der Schlüssel zur Erklärung der Naturgesetze. Beispielsweise weist die Raumzeit hochenergetischer Teilchen eine Lorentzgruppensymmetrie (SO (1, 3)-Gruppe) auf, und äquivariante neuronale Netzwerke der Lorentzgruppe können in Zukunft eine wichtige Rolle in der Hochenergiephysik spielen. Die moderne Physik wird mithilfe der Feldtheorie beschrieben, und die mathematische Sprache dahinter ist auch Differentialgeometrie und Faserbündel. Es ist absehbar, dass tiefes Geometrielernen eine führende Rolle bei der Kombination von moderner Physik und künstlicher Intelligenz spielen wird.
Für das große AI for Science-Modell, das auf geometrischem Deep Learning basiert, können wir eine einfache und mutige Idee entwickeln: Lernen Sie zunächst die Symmetrie des Eingabesystems durch eine Art neuronales Netzwerk, beispielsweise durch Erlernen der Lie-Algebra-Methode der Symmetriegruppe [ 3]; dann durch Ein bestimmter Mechanismus steuert die Stärke verschiedener Symmetrien, sodass das Netzwerk auswählen kann, welche Symmetriegruppe des äquivarianten Netzwerks verwendet werden soll, sodass das Netzwerk die ungefähre Symmetrie des Eingabesystems erfüllen kann. Natürlich ist die Wahrscheinlichkeit groß, dass zukünftige Großmodelle nicht so einfach sein werden, und sie sind auch voller Probleme, die noch gelöst werden müssen. Wir freuen uns darauf, in Zukunft weitere Fortschritte in dieser Richtung zu sehen.
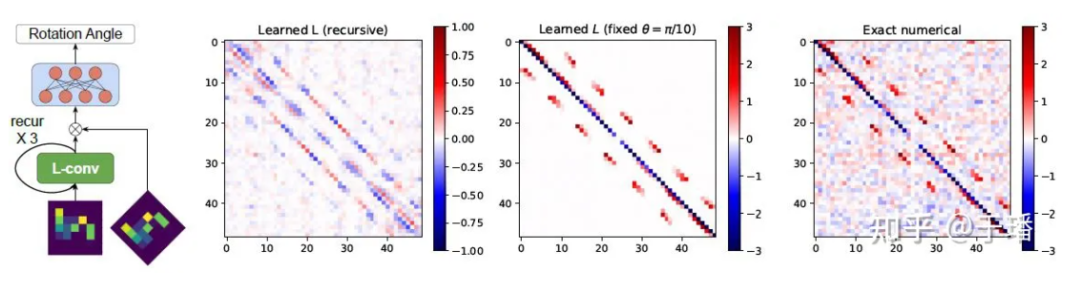
Abbildung 2: Lie-Algebra der SO(2)-Gruppe von L-conv-Lerndaten
Verweise
[1] Bronstein, Michael M., et al. „Geometrisches Deep Learning: Gitter, Gruppen, Diagramme, Geodäten und Messgeräte.“ arXiv-Vorabdruck arXiv:2104.13478 (2021).
[2] Weiler, Maurice et al. „Koordinieren Sie unabhängige Faltungsnetzwerke – Isometrie und eichäquivariante Faltungen auf Riemannschen Mannigfaltigkeiten.“ arXiv-Vorabdruck arXiv:2106.06020 (2021).
[3] Dehmamy N, Walters R, Liu Y, et al. Automatische Symmetrieerkennung mit dem Lie-Algebra-Faltungsnetzwerk[J]. Fortschritte in neuronalen Informationsverarbeitungssystemen, 2021, 34: 2503-2515.
Ein in den 1990er Jahren geborener Programmierer hat eine Videoportierungssoftware entwickelt und in weniger als einem Jahr über 7 Millionen verdient. Das Ende war sehr bestrafend! Google bestätigte Entlassungen, die den „35-jährigen Fluch“ chinesischer Programmierer in den Flutter-, Dart- und Teams- Python mit sich brachten stark und wird von GPT-4.5 vermutet; Tongyi Qianwen Open Source 8 Modelle Arc Browser für Windows 1.0 in 3 Monaten offiziell GA Windows 10 Marktanteil erreicht 70 %, Windows 11 GitHub veröffentlicht weiterhin KI-natives Entwicklungstool GitHub Copilot Workspace JAVA ist die einzige starke Abfrage, die OLTP+OLAP verarbeiten kann. Dies ist das beste ORM. Wir treffen uns zu spät.
