Teilhaber: Jin Sui｜Schule**: University of Electronic Science and Technology of China**
kurze Einleitung
Quantencomputing verspricht für viele spezifische Aufgaben eine höhere Rechenleistung als klassisches Computing. Allerdings sind laute Quantencomputer noch nicht vollständig fehlertolerant, was auch zu Zweifeln an der Praktikabilität des aktuellen Quantencomputings geführt hat. Jüngste Arbeiten von IBM haben Experimente mit einem lauten 127-Qubit-Prozessor ermöglicht und Fähigkeiten demonstriert, die über das klassische Rechnen hinausgehen. Diese experimentellen Ergebnisse profitieren von Fortschritten in der Kohärenz und Kalibrierung in großen supraleitenden Prozessoren sowie von der Fähigkeit, Rauschen auf solch großen Geräten zu charakterisieren und zu kontrollieren. In stark verschränkten Zuständen liefern Quantencomputer korrekte Ergebnisse, während gängige klassische Näherungsverfahren wie MPS und Iso-TNS versagen. Diese Experimente haben die Fähigkeit moderner Quantencomputer gezeigt, praktische Probleme zu lösen.
Verwandte Artikel
**Mehr: Beweise für den Nutzen von Quantencomputern vor Fehlertoleranz
作者**Youngseok Kim, Andrew Eddins, Sajant Anand, Ken Xuan Wei, Ewout van den Berg, Sami Rosenblatt, Hasan Nayfeh, Yantao Wu, Michael Zaletel, Kristan Temme & Abhinav Kandala
**Zeitschrift:**Nature Band 618, Seiten 500–505 (2023)
**Veröffentlichungsdatum:** 14. Juni 2023
01
Einführung
Es wird allgemein angenommen, dass fortgeschrittene Quantenalgorithmen wie Faktorisierung oder Phasenschätzung eine Quantenfehlerkorrektur erfordern, um ihre Vorteile zu demonstrieren. Allerdings wird heftig darüber diskutiert, ob derzeit verfügbare Prozessoren andere flache Quantenschaltungen zuverlässig genug ausführen können, um Vorteile bei praktischen Problemen zu bieten.
Der Nachweis des Quantenvorteils kann durch den Nachweis erreicht werden, dass vorhandene Quantengeräte in der Lage sind, präzise Berechnungen durchzuführen, die über klassische Simulationen hinausgehen. Diese Arbeit konzentriert sich darauf, die Vorteile des Quantencomputings zu demonstrieren, anstatt Quantenschaltungen für Probleme zu implementieren, für die Beschleunigung nachgewiesen wurde.
02
** IBM Quantum-Prozessor
**
Diese Arbeit verwendet einen supraleitenden 127-Qubit-Quantenprozessor, um das zweidimensionale Transversalfeld-Ising-Modell zu simulieren. Seine Schaltungstiefe umfasst 60 Schichten von Zwei-Bit-Quantengattern, und die Gesamtzahl der CNOT-Gatter beträgt 2.880. Der in diesem Artikel verwendete Quantenprozessor ist ibm_kyiv.
(Quelle: Originalpapier)
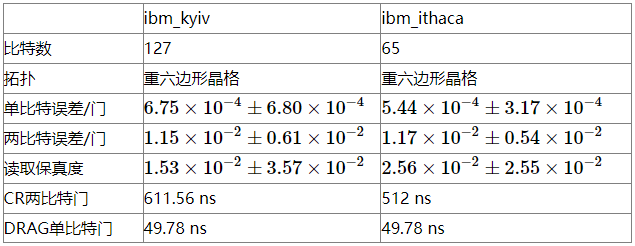
1) Die Medianwerte von T1 und T2 betragen 287,87 μs bzw. 127,49 μs.
2) Der durchschnittliche Fehler eines einzelnen Bits liegt in der Größenordnung von 10–4 und der durchschnittliche Fehler von zwei Bits liegt in der Größenordnung von 10–. 2;
3) Die Lesegenauigkeit liegt jeweils in der Größenordnung von 10 -2.
03
Aufgaben, die Quantencomputer übernehmen
In diesem Artikel wird hauptsächlich der Quantenprozessor ibm_kyiv verwendet, um die Entwicklung des zweidimensionalen Transversalfeld-Ising-Modells zu simulieren. Die Form seines Hamilton-Operators ist:
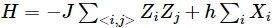
Dabei ist J die Kopplungsstärke zwischen den nächsten Nachbarn und h die globale Querfeldstärke. Die Nächste-Nachbarn-Beziehung dieses Modells basiert auf der Struktur des Quantenprozessors selbst, wie in Abbildung 1b unten dargestellt.
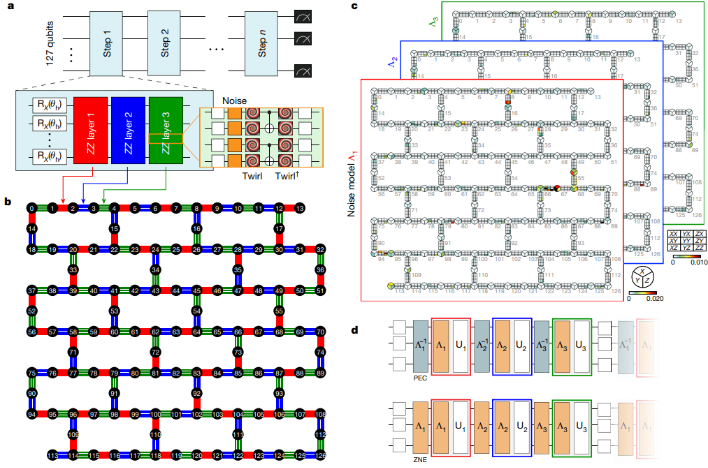
Abbildung 1 (Quelle: Originalpapier)
Diese einheitliche Entwicklung kann durch Trotter-Zerlegung erster Ordnung angenähert werden.
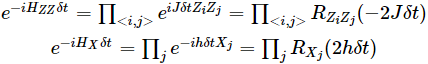
Zur Vereinfachung der Implementierung wird es hier so ausgewählt , dass das ZZ-Rotationsgatter der folgenden Quantenschaltung entsprechen kann, die nur ein CNOT benötigt:
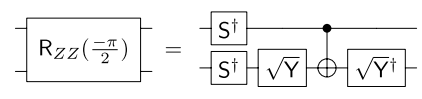
Wir können das ZZ-Rotationsgatter entsprechend der Struktur des Quantenprozessors selbst in drei parallele Schichten unterteilen, wie in den Abbildungen a und b gezeigt, was bedeutet, dass jeder Schritt des Trabers drei Schichten von CNOT-Gattern enthält. Aus der Abbildung ist ersichtlich, dass für jeden Traberschritt 144 CNOT-Gates erforderlich sind. Wenn die Quantenschaltung 20 Traberschritte ausführt, also 60 Schichten von CNOT-Gattern, erreicht sie die im Artikel erwähnte Anzahl von CNOT-Gattern, 2880.
04
** Geräuschmodell
**
Das in diesem Artikel ausgewählte Rauschmodell ist das Sparse Pauli-Linblad-Rauschmodell.
Die Rauschschicht ist in Abbildung 1 c,d dargestellt. In diesem Artikel werden Ebenen vor der ursprünglichen Rauschebene 
hinzugefügt 
, um die Größe des Rauschens zu steuern. Zu diesem Zeitpunkt beträgt der gesamte Rauschkanal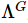 
, wobei G der Verstärkungsfaktor ist 
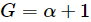. Bei der Zero-Noise-Extrapolation (ZNE) verstärken die Autoren das Rauschen auf unterschiedliche Verstärkungsstufen und nutzen die Extrapolation, um das Null-Rauschen abzuschätzen.
Hier wählt dieser Artikel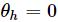 
nämlich aus 
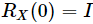. Zu diesem Zeitpunkt wirkt die gesamte Schaltung auf den 0-Zustand und ändert den Quantenzustand nicht, sodass 
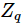der erwartete Wert, der durch Verwendung der zu messenden Beobachtungsgröße erhalten wird, 1 ist. Abbildung 2 unten zeigt die experimentellen Ergebnisse bei unterschiedlichen Rauschpegeln, unterschiedlichen Schaltungstiefen und nach ZNE.
Abbildung 2 (Quelle: Originalarbeit)
Abbildung 2a ist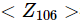 
das Ergebnis der Durchführung und Beobachtung des 4-Schritt-Trabers. Es ist ersichtlich, dass ZNE die Auswirkungen von Lärm effektiv reduzieren und relativ genaue Beobachtungswerte erhalten kann. Darüber hinaus ist der Effekt der exponentiellen Extrapolation im Allgemeinen besser als der der linearen Extrapolation. Abbildung c zeigt 
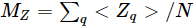die Beziehung zwischen dem Durchschnittswert jeder Qubit-Beobachtung und der Schaltkreistiefe. Der Fehler der Ergebnisse ohne Fehlerminderung wird mit zunehmender Schaltungstiefe größer, während nach Fehlerminderung immer noch genauere Ergebnisse erzielt werden können.
05
****Experimentelles Beispiel
**
**
(1) 5-Stufen-Traber, 15-lagiger CNOT
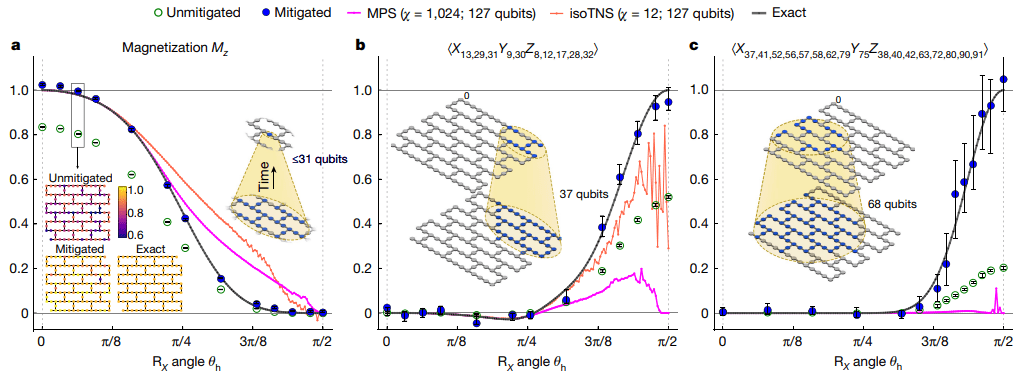
Abbildung 3 (Quelle: Originalpapier)
In diesem Beispiel verwendet dieser Artikel die Beobachtungen Gewicht 1, Gewicht 10 und Gewicht 17, um den Quantenschaltkreis des 5-Stufen-Trabers zu messen. Die experimentellen Ergebnisse sind in der Abbildung dargestellt. Bei der Durchführung klassischer Simulationen zur Erzielung genauer Lösungen wird hier die Light-Cone-and-Depth-Reduced-Methode (LCDR) verwendet. Es ist in zwei Teile unterteilt: Ein Teil besteht darin, die Anzahl der Schaltungsschichten zu reduzieren, die durch die Eigenschaften zwischen Quantengattern simuliert werden müssen. Der andere Teil besteht darin, zu berücksichtigen, dass die mit der Beobachtungsgröße A verbundenen Qubits lokal sind Anstelle aller 127 Bits muss dann nur ein Teil der Qubits berücksichtigt werden.
Wie in Abbildung 3 dargestellt, betragen die zugehörigen Qubit-Zahlen der Beobachtungen der Gewichtung 1, der Gewichtung 10 und der Gewichtung 17 jeweils 31, 37 und 68. Es ist erwähnenswert, dass die Simulation mit 68 Qubits immer noch über den Möglichkeiten von Brute-Force-Simulationen durch klassische Computer liegt. Daher werden in diesem Artikel Tensornetzwerke, 1D-Matrixproduktzustände (MPS) und 2D-isometrische Tensornetzwerkzustände (iso TNS) zur Simulation vorgestellt. Ihre Komplexität ist
Dabei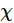 
ist die Bindungsdimension und M die Anzahl der Bits.
In diesem Beispiel muss MPS die Bindungsdimension übernehmen,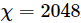 
um genaue Ergebnisse zu simulieren. Aus der Abbildung ist ersichtlich, dass die experimentellen Ergebnisse nach der Fehlerminderung näher an den tatsächlichen Ergebnissen liegen.
(2) Fügen Sie am Ende eine Single-Bit-Drehtür und einen 5-Stufen-Traber hinzu
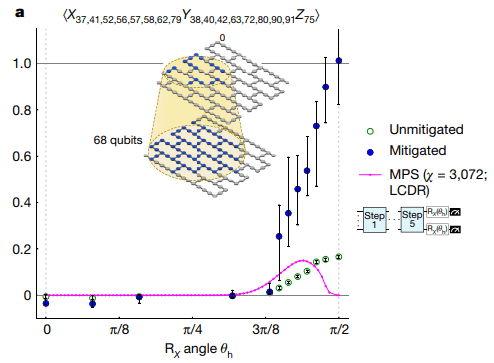
(Quelle: Originalpapier)
Dieses Beispiel unterscheidet sich vom vorherigen dadurch, dass am Ende eine Schicht aus Einzelbit-Drehkreuzen hinzugefügt wird, was zu einer geringeren Unterbrechungstiefe im Schaltkreis führt. Der Autor verwendet für die Messung Beobachtungen mit einer Gewichtung von 17, und die Anzahl der damit verbundenen Qubits beträgt 68. Dies ist erforderlich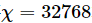 
, um diesen Evolutionsprozess genau zu simulieren.
(3) 20-stufiger Traber, 60-lagiger CNOT
(Quelle: Originalpapier)
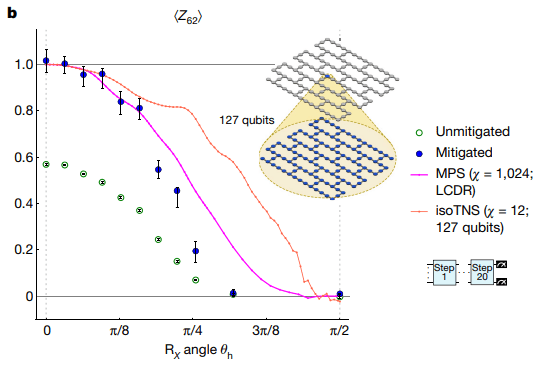
Obwohl hier nur Beobachtungen der Gewichtung 1 zur Messung verwendet werden, erreicht die Anzahl der damit verbundenen Qubits aufgrund der großen Anzahl von Schichten (20-Schritte-Trotter) 127. Daher ist es sehr schwierig, diesen Evolutionsprozess zu simulieren. Die Verwendung von MPS zur Simulation erfordert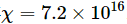 
genaue Ergebnisse. Beispielsweise gibt es ein System, das eine Extraktion der Bindungsdimensionen erfordert 
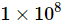. Da die zum Speichern von MPS erforderliche Speichergröße beträgt 
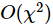, beträgt der erforderliche Speicher unabhängig von anderen Faktoren 400 PB.
Obwohl es keine exakte Lösung als Maß gibt, zeigen diese beiden Beispiele dennoch, dass Fehlerminderungstechniken für Quantenschaltungen dieser Größe und Tiefe immer noch wirksam sind.
06
Zusammenfassen
Viele Quantenalgorithmen sind durch den Einfluss von Rauschen in aktuellen Quantencomputern eingeschränkt und können ihre Vorteile nicht effektiv ausspielen. Derzeitige verrauschte Quantencomputer sind jedoch noch nicht vollständig fehlertolerant. Mit der Arbeit von IBM gelang es diesmal, das 2D-Transversalfeld-Ising-Modell auf 127 Quantenprozessoren zu simulieren und zu zeigen, dass verrauschte Quantencomputer immer noch zuverlässige Erwartungen ausgeben können. Dies bietet neue Forschungsrichtungen für nachfolgende Forscher.
Ein in den 1990er Jahren geborener Programmierer hat eine Videoportierungssoftware entwickelt und in weniger als einem Jahr über 7 Millionen verdient. Das Ende war sehr bestrafend! Google bestätigte Entlassungen, die den „35-jährigen Fluch“ chinesischer Programmierer in den Flutter-, Dart- und Teams- Python mit sich brachten stark und wird von GPT-4.5 vermutet; Tongyi Qianwen Open Source 8 Modelle Arc Browser für Windows 1.0 in 3 Monaten offiziell GA Windows 10 Marktanteil erreicht 70 %, Windows 11 GitHub veröffentlicht weiterhin KI-natives Entwicklungstool GitHub Copilot Workspace JAVA ist die einzige starke Abfrage, die OLTP+OLAP verarbeiten kann. Dies ist das beste ORM. Wir treffen uns zu spät.