Auteur : Yu Fan
arrière-plan
Les systèmes spatio-temporels complexes modélisés par des équations aux dérivées partielles sont omniprésents dans de nombreuses disciplines, telles que les mathématiques appliquées, la physique, la biologie, la chimie et l'ingénierie. Dans la plupart des cas, nous ne sommes pas en mesure d'obtenir des solutions analytiques aux EDP utilisées pour décrire ces systèmes physiques complexes, c'est pourquoi les méthodes de résolution numérique ont été étudiées de manière approfondie, notamment : les éléments finis, les différences finies, l'analyse isogéométrique (IGA) et d'autres méthodes. Bien que ces méthodes numériques traditionnelles puissent se rapprocher de la solution exacte de l’équation grâce à des fonctions de base, l’assimilation des données et la résolution du problème inverse représentent encore une énorme charge de calcul.
Ces dernières années, diverses méthodes d'apprentissage profond ont émergé en continu pour résoudre les problèmes directs et inverses des systèmes non linéaires. La recherche sur l'utilisation du DNN pour modéliser des systèmes physiques peut être grossièrement divisée en deux catégories : les réseaux continus et les réseaux discrets. Les PINN sont un représentant typique des réseaux continus : le résidu de PDE est utilisé comme contrainte douce du réseau neuronal, et une couche entièrement connectée est utilisée pour approximer la solution de l'équation, et le modèle peut être réalisé à petite échelle de données ou même des données échantillonnées non étiquetées. Néanmoins, les PINN sont souvent limités à des paramétrisations de faible dimension et sont étirés lorsqu'ils sont confrontés à des systèmes PDE présentant des gradients abrupts et des morphologies locales complexes. Récemment, un petit nombre d'études pilotes ont montré que les réseaux discrets ont une meilleure évolutivité et une vitesse de convergence plus rapide que l'apprentissage continu. Par exemple, CNN peut être utilisé comme modèle proxy dans le domaine rectangulaire pour les systèmes indépendants du temps qui utilisent des systèmes physiques et de référence. Pour résoudre de manière géométriquement adaptative des équations aux dérivées partielles en régime permanent par transformation de coordonnées, pour les systèmes dépendants du temps, la plupart des méthodes de résolution de réseaux neuronaux sont toujours basées sur les données et le maillage.
PhyCRNet[1], proposé par l'équipe du professeur Sun Hao de la Hillhouse School of Artificial Intelligence de l'Université Renmin de Chine, en collaboration avec la Northeastern University (États-Unis) et l'Université de Notre Dame, est une méthode non supervisée pour résoudre des PDE dans des domaines spatio-temporels multidimensionnels. grâce à des connaissances physiques préalables et à une architecture de réseau récursive convolutionnelle, qui combine ConvLSTM (extraction de caractéristiques spatiales de faible dimension et apprentissage de l'évolution temporelle), connexion résiduelle globale (cartographie stricte des changements dans les solutions d'équation sur l'axe du temps) et différence finie d'ordre élevé. le filtrage spatio-temporel (déterminant la construction d'une fonction de perte résiduelle et la capacité des dérivées PDE requises) en fait une solution de base face à des problèmes inverses et lorsque les données sont rares et bruitées.
1. Définition du problème
Considérant les équations aux dérivées partielles paramétriques non linéaires multidimensionnelles, la forme générale est la suivante :
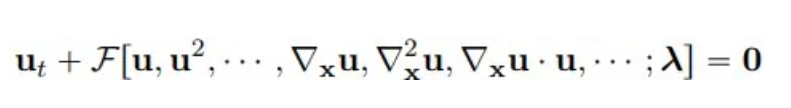
où u(x, t) représente la solution de l'équation dans le domaine temporel T et le domaine spatial Ω, et F est une fonctionnelle non linéaire de paramètre λ.
**2. ** Méthode modèle
ConvLSTM
ConvLSTM est un cadre d'apprentissage spatio-temporel séquence à séquence qui s'étend du LSTM et de sa variante d'architecture de prédiction codeur-décodeur LSTM (qui ont l'avantage de modéliser des dépendances sur de longues périodes qui évoluent au fil du temps). Essentiellement, l'unité de mémoire est mise à jour avec l'accès aux informations d'entrée et d'état, et l'accumulation et l'effacement de la mémoire sont effectués via des portes de contrôle intelligemment conçues. Sur la base de ce paramètre, le problème de disparition de gradient des réseaux neuronaux récurrents (RNN) ordinaires est atténué. ConvLSTM hérite de la structure de base du LSTM (c'est-à-dire les unités cellulaires et les portes) pour contrôler le flux d'informations et modifie le réseau neuronal entièrement connecté (FC-NN) pour tenir compte du fait que CNN a de meilleures capacités de représentation de connexion spatiale et effectue des opérations de déclenchement sur CNN. . En tant que type spécial de RNN, LSTM peut être utilisé comme méthode numérique implicite pour résoudre des équations PDE dépendant du temps. Le schéma de structure d'une seule unité ConvLSTM est le suivant :
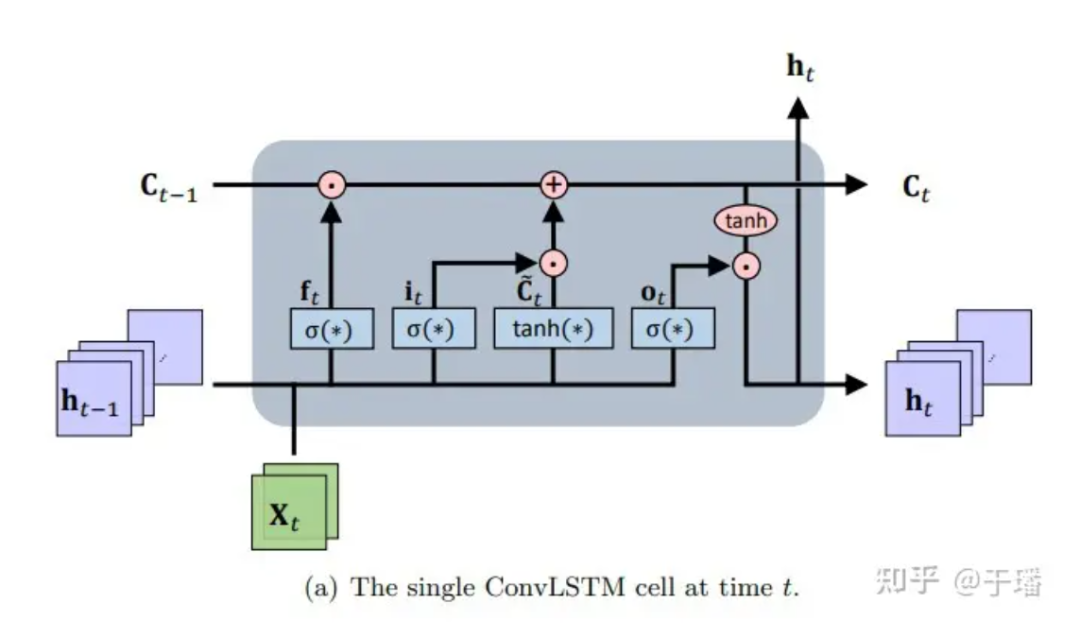Figure 1 : Cellule ConvLSTM unique au temps t
La représentation mathématique de la mise à jour d'une unité ConvLSTM est la suivante :
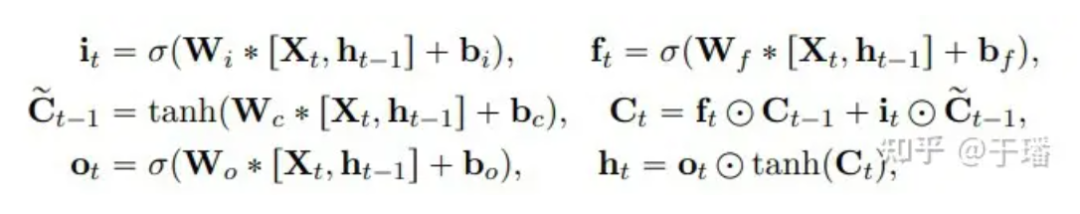
Parmi eux, * représente l'opération de convolution, ⊙ représente le produit Hadamard ; W est le paramètre de poids du filtre et b représente le vecteur biais.
Mélange de pixels
Pixel Shuffle est une opération de convolution de sous-pixels efficace qui suréchantillonne une image basse résolution (LR) en une image haute résolution (HR). Supposons que les dimensions d'un tenseur de caractéristiques LR sont (C Un tenseur HR avec des dimensions (C, H xr, W xr).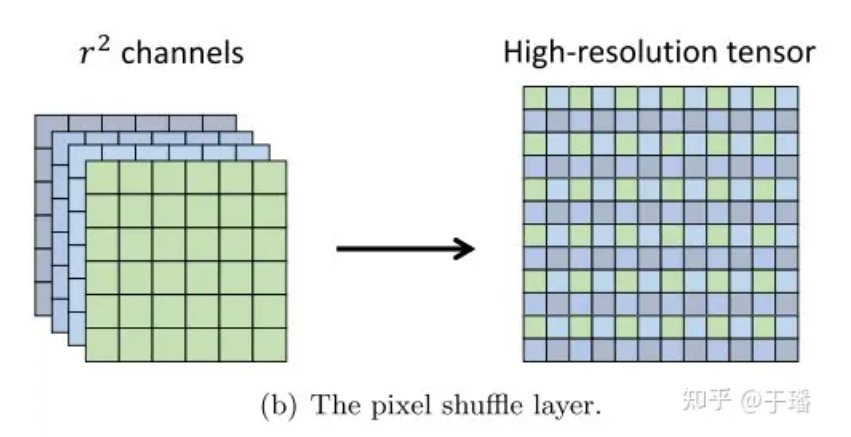 
Figure 2 : calque Pixel Shuffle
L'efficacité de Pixel Shuffle se reflète dans : (1) l'augmentation uniquement de la résolution dans la dernière couche de convolution, ce qui peut éviter d'avoir à utiliser davantage de couches de convolution pour augmenter l'image à la résolution cible telle que la déconvolution (2) ) Dans ; toutes les couches d'extraction de caractéristiques avant la couche de suréchantillonnage, des filtres plus petits peuvent être utilisés pour traiter ces tenseurs basse résolution.
PhyCRNet
PhyCRNet se compose de modules codeurs-décodeurs, de connexions résiduelles, de processus autorégressifs et d'une méthode différentielle basée sur des filtres. L'encodeur contient trois couches convolutives pour apprendre les caractéristiques latentes de basse dimension de la variable d'état Ui à un moment donné et la laisser évoluer au fil du temps via ConvLSTM. Étant donné que la transformation est effectuée sur des variables de faible dimension, la surcharge mémoire sera réduite en conséquence. De plus, en s'inspirant de la méthode d'Euler directe, nous pouvons ajouter une connexion résiduelle globale entre la variable d'entrée Ui et la variable de sortie Ui+1, et le processus d'apprentissage en une seule étape peut être exprimé comme Ui+1 = Ui + δt x N [Ui ; θ], où N[·] représente l'opérateur de réseau neuronal formé, et δt est l'intervalle de temps unitaire. Par conséquent, cette relation récursive peut être considérée comme un simple processus autorégressif.
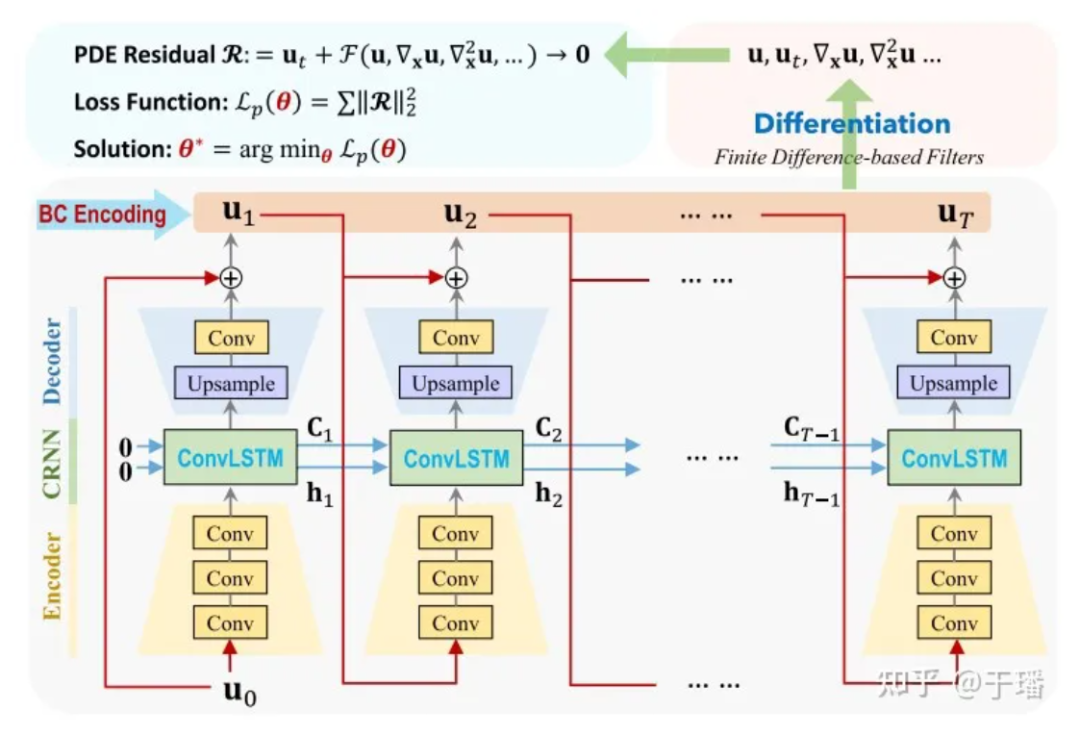Figure 3 : Diagramme de structure du réseau PhyCRNet
Ici, U0 est la condition initiale, U1 à UT sont les solutions discrètes qui doivent être prédites par le modèle et l'évolution temporelle de l'entrée à la sortie. Par rapport aux méthodes numériques traditionnelles, ConvLSTM peut utiliser un intervalle de temps plus grand. Pour le calcul de chaque terme différentiel, nous utilisons un noyau de convolution fixe [1] pour représenter leurs valeurs de différence. Dans PhyCRNet, les termes de différence du deuxième et du quatrième ordre sont utilisés pour calculer les dérivées de U par rapport au temps et à l'espace. Afin d'optimiser davantage les performances de calcul, nous pouvons sauter la partie codeur dans un cycle de taille T, à l'exception du premier instant de chaque cycle. Le schéma schématique est le suivant :
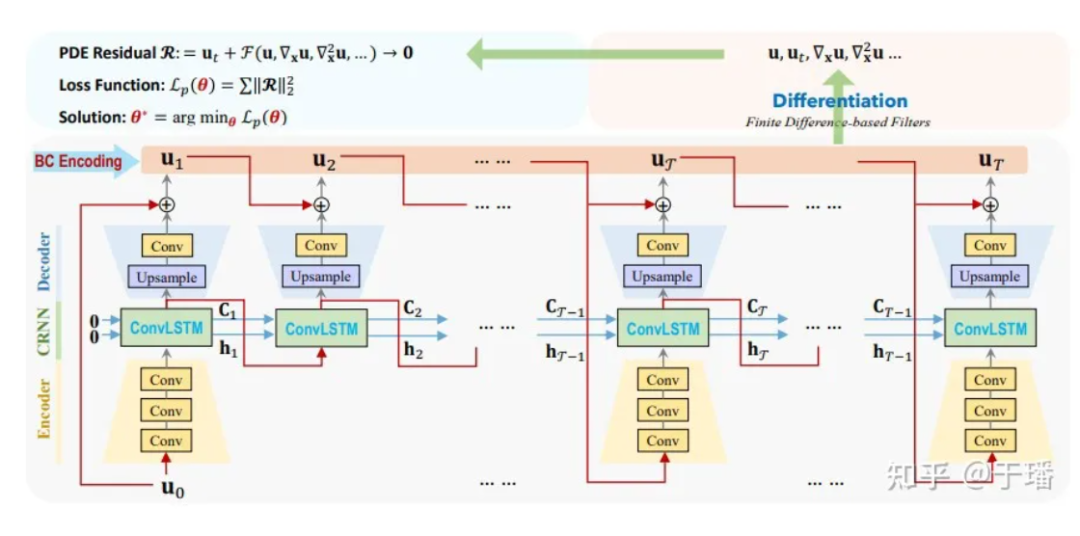Figure 4 : Diagramme de structure du réseau PhyCRNet
Contraintes strictes I/BC
Par rapport à la méthode PINNs, qui utilise les conditions aux limites physiques initiales comme contraintes souples (ses résidus sont optimisés dans le cadre de la perte), PhyCRNet utilise la méthode de codage en dur I/BC dans le modèle (les conditions initiales sont utilisées comme entrée U0 de ConvLSTM, et les conditions aux limites sont codées via un remplissage), de sorte que les conditions physiques ne soient plus une contrainte douce, améliorant ainsi la précision et la vitesse de convergence du modèle. Pour Dirichlet BC, les valeurs limites constantes connues peuvent être remplies directement comme remplissage dans le domaine spatial ; tandis que pour Neumann BC, une couche d'éléments fantômes peut être ajoutée autour du domaine spatial (éléments fantômes), leurs valeurs sont. approximée par les différences au cours du processus de formation.
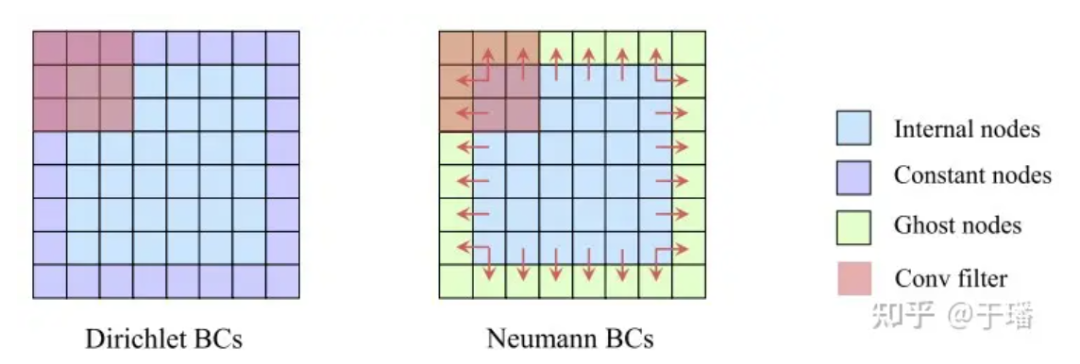Figure 5 : Illustration de contraintes dures sur les conditions aux limites
fonction de perte
Étant donné que I/BC a été strictement contraint dans le modèle, la fonction de perte n'a besoin d'inclure que le terme résiduel de l'EDP. En prenant comme exemple un système d'EDP bidimensionnel, la fonction de perte peut être exprimée comme suit :
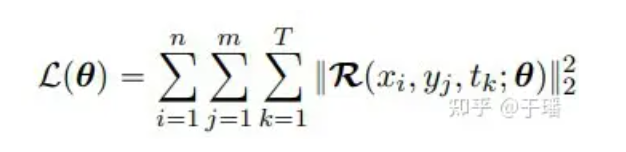
où n et m représentent la hauteur et la largeur de la grille, T est le nombre total de pas de temps et R(x, t; θ) est le résidu de PDE :
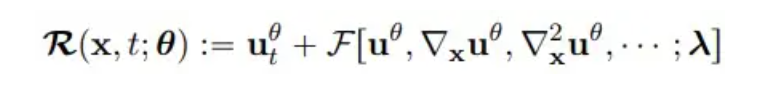
**3. ** Analyse des résultats
Pour évaluer l'erreur du modèle dans l'ensemble du domaine, l'erreur quadratique moyenne cumulée (a-RMSE) au temps τ est calculée comme suit :
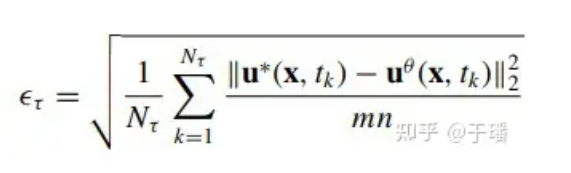
où Nτ est le nombre de pas de temps dans [0, τ] et u*(x, t) est la solution de référence de l'équation.
Équation de Burgers bidimensionnelle
Considérons un problème classique en mécanique des fluides, étant donné l’équation de Burgers bidimensionnelle de la forme suivante :
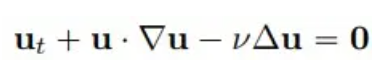
Nous sélectionnons 4 points temporels : formation (t = 1,0, 2,0) et extrapolation (t = 3,0, 4,0) pour comparer la précision de la solution et les capacités d'extrapolation des méthodes PhyCRNet et PINN :
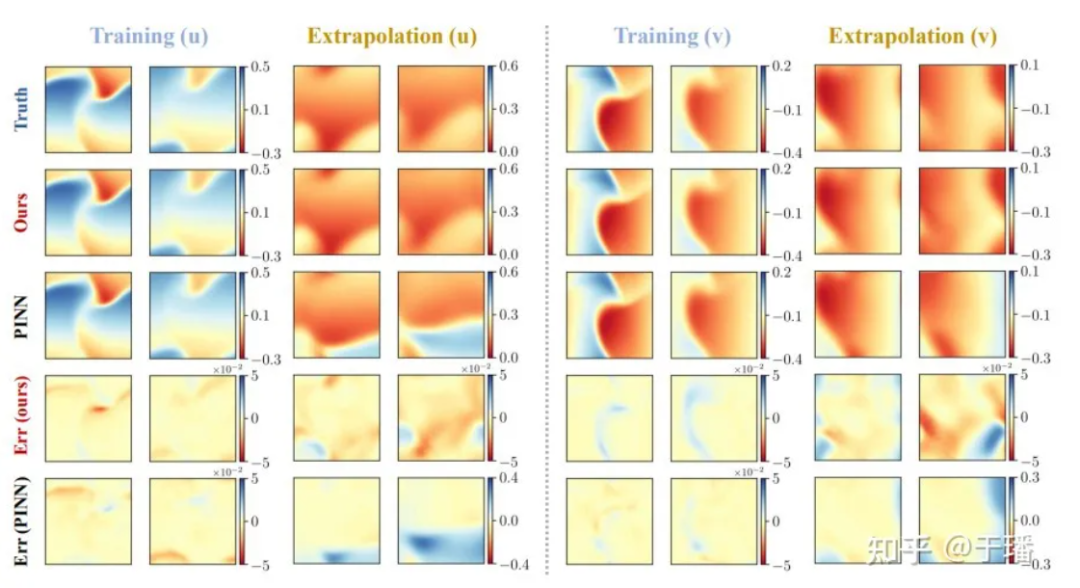Figure 6 : Résultats de formation et d'extrapolation de PhyCRNet par rapport aux PINN pour l'équation de Burgers bidimensionnelle
Équation λ-ω RD
Dans un deuxième cas, considérons un système λ-ω RD bidimensionnel (souvent utilisé pour représenter des processus biochimiques à plusieurs échelles) :
Parmi eux, u et v sont deux variables de champ qui satisfont :
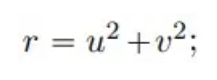
λ et ω sont deux fonctions à valeur réelle :
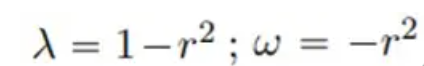
La solution de référence pour un total de 801 pas de temps dans la zone [-10, 10] est générée par la méthode spectrale après un entraînement pendant 200 pas de temps dans la période de temps [0, 5], la solution de référence pour [5, 10 ; ] La prédiction est effectuée au cours de la période, et les résultats de prédiction comparant PhyCRNet et PINN sont les suivants :
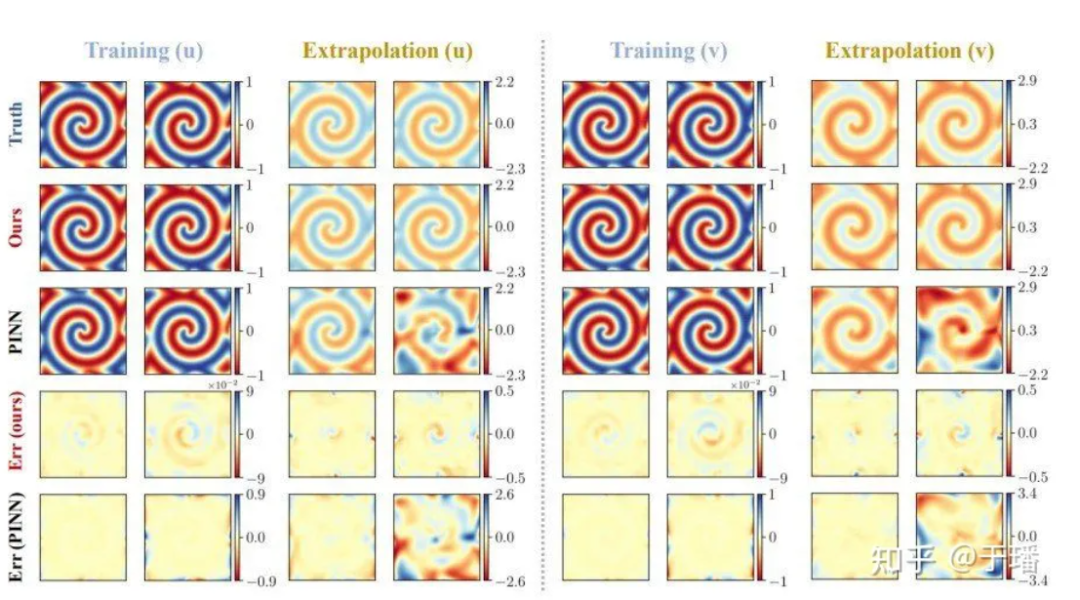Figure 7 : Résultats de formation et d'extrapolation PhyCRNet vs PINN pour l'équation λ-ω RD
La figure ci-dessous montre les courbes de propagation des erreurs de PhyCRNet et des PINN lors de la formation et de l'extrapolation dans les deux systèmes PDE mentionnés ci-dessus. On voit clairement que PhyCRNet fonctionne mieux dans les deux étapes (en particulier l'étape d'extrapolation).
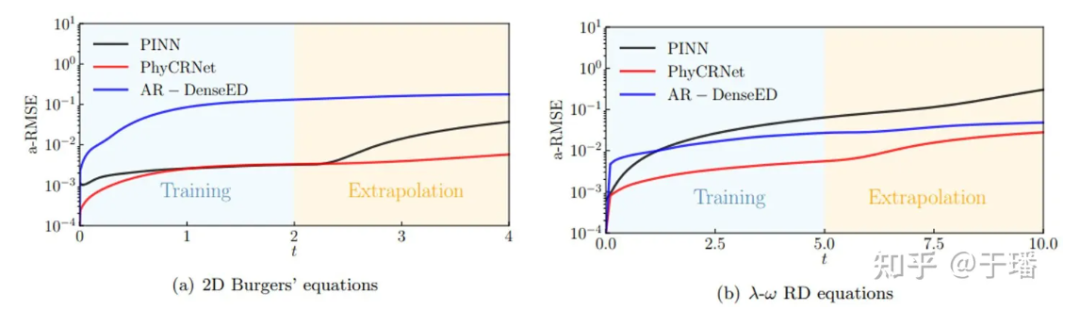Figure 8 : Comparaison de la propagation des erreurs de PhyCRNet et des PINN
les références
[1] Ren P, Rao C, Liu Y et al. PhyCRNet : réseau convolutionnel-récurrent informé par la physique pour résoudre les PDE spatio-temporelles [J]. Méthodes informatiques en mécanique appliquée et ingénierie, 2022, 389 : 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
Un programmeur né dans les années 1990 a développé un logiciel de portage vidéo et en a réalisé plus de 7 millions en moins d'un an. La fin a été très éprouvante ! Google a confirmé les licenciements, impliquant la « malédiction des 35 ans » des codeurs chinois des équipes Flutter, Dart et . Python Arc Browser pour Windows 1.0 en 3 mois officiellement la part de marché de GA Windows 10 atteint 70 %, Windows 11 GitHub continue de décliner l'outil de développement natif d'IA GitHub Copilot Workspace JAVA. est la seule requête de type fort capable de gérer OLTP+OLAP. C'est le meilleur ORM. Nous nous rencontrons trop tard.