Auteur : Yu Fan
arrière-plan
Le développement de l’intelligence artificielle (IA) a introduit un nouveau paradigme dans la découverte scientifique. Aujourd’hui, l’IA a commencé à améliorer, accélérer et permettre notre compréhension des phénomènes naturels sur un large éventail d’échelles spatiales et temporelles, favorisant ainsi le développement des sciences naturelles et donnant naissance au nouveau domaine de recherche AI4Science. Récemment, un article de synthèse « Intelligence artificielle pour la science dans les systèmes quantiques, atomiques et continus » rédigé conjointement par plus de 60 auteurs fournit un résumé technique approfondi dans les sous-domaines des systèmes subatomiques, atomiques et continus. Nous extrayons ici l'épine dorsale technique de cette revue et nous concentrons sur la façon de construire un modèle équivariant sous transformation de symétrie.
1. Introduction
En 1929, le physicien quantique Paul Dirac notait : « Les lois physiques fondamentales nécessaires à la théorie mathématique de la majeure partie de la physique et de l'ensemble de la chimie nous sont déjà parfaitement connues, et la difficulté réside dans le fait que l'application précise de ces lois conduit à complexe Cela est vrai de l'équation de Schrödinger en physique quantique à l'équation de Navier-Stokes en mécanique des fluides. L’apprentissage profond peut accélérer la résolution de ces équations. En utilisant les résultats des méthodes de simulation traditionnelles comme données de formation, une fois formés, ces modèles peuvent faire des prédictions beaucoup plus rapidement que la simulation traditionnelle.
Dans d’autres domaines, comme la biologie, les processus biophysiques sous-jacents peuvent ne pas être entièrement compris et, en fin de compte, ne pas être décrits par des équations mathématiques. Dans ces cas, les modèles d'apprentissage profond peuvent être formés à l'aide de données générées expérimentalement, telles que les modèles de prédiction de protéines AlphaFold, RoseTTAFold, ESMFold et d'autres structures 3D obtenues par des expériences, de sorte que la précision des structures 3D de protéines prédites par ordinateur puisse être comparable aux résultats expérimentaux. .
1.1 Domaines scientifiques
Les domaines d’intérêt scientifique de cet article sont organisés de manière synthétique dans la figure ci-dessous, en fonction des échelles spatiales et temporelles du système physique modélisé.
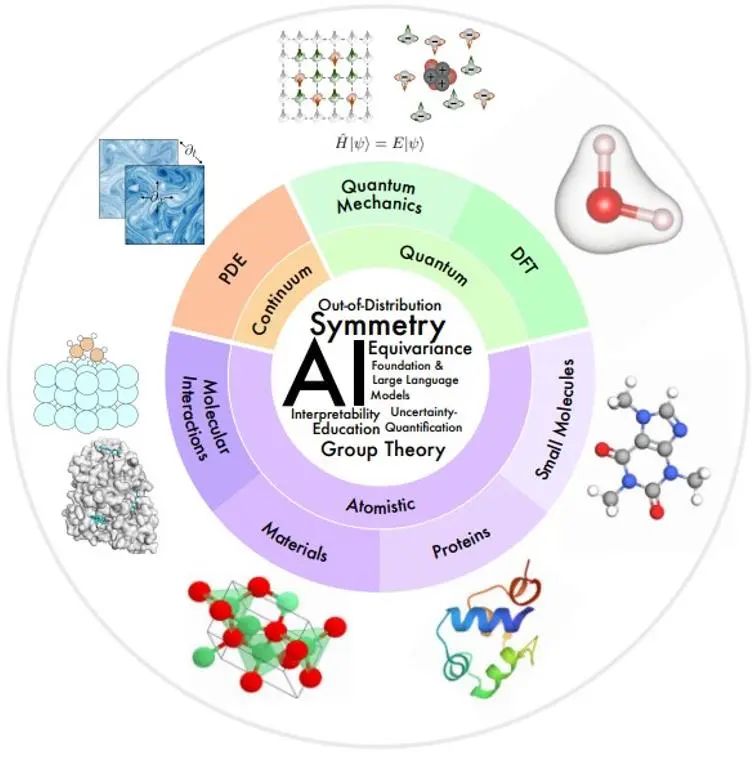
Petite échelle : la mécanique quantique utilise la fonction d'onde pour étudier les phénomènes physiques à la plus petite échelle. L'équation de Schrödinger à laquelle elle obéit décrit le processus dynamique complet du système quantique, mais elle apporte une complexité exponentielle. La théorie fonctionnelle de la densité (DFT) et les méthodes de chimie quantique ab initio sont des méthodes de principes fondamentaux largement utilisées dans la pratique pour calculer la structure électronique et les propriétés physiques des molécules et des matériaux, et peuvent en déduire davantage les propriétés électroniques et mécaniques des molécules et des solides, optiques. , propriétés magnétiques et catalytiques. Cependant, ces méthodes restent coûteuses en termes de calcul, limitant leur utilisation aux petits systèmes (~ 1 000 atomes). Le modèle d'IA peut contribuer à améliorer la vitesse et la précision.
Méso-échelle : les petites molécules, généralement de plusieurs dizaines à centaines d'atomes, jouent des rôles importants de régulation et de signalisation dans de nombreux processus chimiques et biologiques. Les protéines sont de grosses molécules composées d'une ou plusieurs chaînes d'acides aminés. La séquence d’acides aminés détermine la structure des protéines, qui à son tour détermine leur fonction. La recherche en science des matériaux étudie la relation entre le traitement, la structure, les propriétés et les matériaux. Les interactions moléculaires étudient le nombre de fonctions physiques et biologiques exécutées par le biais d'interactions moléculaires, telles que les interactions ligand-récepteur et molécule-matériau. Dans ces domaines, l’IA a réalisé de nombreux progrès en matière de caractérisation et de génération moléculaires, de dynamique moléculaire, de prédiction et de conception de la structure des protéines, de prédiction des propriétés des matériaux et de génération de structures.
À grande échelle : la mécanique des milieux continus utilise des équations aux dérivées partielles pour modéliser les processus physiques qui évoluent dans le temps et dans l'espace au niveau macroscopique, notamment l'écoulement des fluides, le transfert de chaleur, les ondes électromagnétiques, etc. Les méthodes d'IA apportent des solutions à des problèmes tels que l'amélioration de l'efficacité informatique, la généralisation et l'analyse multi-résolution.
1.2 Domaine technologique de l'IA
Il existe un ensemble commun de défis techniques dans plusieurs domaines de l’IA scientifique.
**Symétrie :**La symétrie est une paranoïa inductive très forte. L'un des défis clés pour AI4Science est donc de savoir comment intégrer efficacement la symétrie dans les modèles d'IA.
**Interprétabilité :**L'interprétabilité est cruciale dans AI4Science pour comprendre les lois du monde physique.
**Généralisation et causalité hors distribution (OOD) : **Pour éviter de générer des données de formation pour chaque contexte différent, les facteurs causals qui permettent la généralisation de l'OOD doivent être identifiés.
**Modèles de base et grands modèles de langage :**Les modèles de base dans les tâches de traitement du langage naturel sont pré-entraînés sous supervision auto-supervisée ou généralisable pour effectuer diverses tâches en aval de manière ponctuelle ou nulle. L’article donne une perspective sur la manière dont ce paradigme peut accélérer les découvertes AI4Science.
**Quantification de l'incertitude (UQ) : **Étudie comment garantir une prise de décision solide dans des conditions d'incertitude des données et des modèles.
**Éducation :** Pour faciliter l'apprentissage et l'éducation, cet article fournit une liste catégorisée de ressources que l'auteur trouve utiles et donne des perspectives sur la façon dont la communauté peut mieux promouvoir l'intégration de l'IA avec la science et l'éducation.
**2. ** Symétrie, équivariance et leurs théories
Dans de nombreux problèmes scientifiques, l'objet d'intérêt est généralement situé dans un espace 3D et toute représentation mathématique de l'objet repose sur un système de coordonnées de référence, ce qui rend une telle représentation relative au système de coordonnées. Cependant, les systèmes de coordonnées n’existent pas dans la nature, une représentation indépendante du système de coordonnées est donc nécessaire. Par conséquent, l’un des principaux défis d’AI4Science est de savoir comment obtenir l’invariance ou l’équivariance sous transformation du système de coordonnées.
2.1 Aperçu
La symétrie fait référence au fait que les propriétés d'un phénomène physique restent inchangées sous certaines transformations, telles que les transformations de coordonnées. Si certaines symétries existent dans le système, la cible de prédiction est naturellement invariante ou équivariante sous la transformation de symétrie correspondante. Par exemple, lors de la prédiction de l'énergie d'une molécule 3D, la valeur prédite reste inchangée lorsque la molécule 3D est soumise à une translation ou à une rotation. Une stratégie alternative pour parvenir à un apprentissage sensible à la symétrie consiste à utiliser l'augmentation des données dans l'apprentissage supervisé, en appliquant spécifiquement des transformations de symétrie aléatoires aux données d'entrée et aux étiquettes pour forcer le modèle à produire des prédictions approximativement équivariantes. Mais cela présente de nombreux inconvénients :
1) Compte tenu des degrés de liberté supplémentaires dans la sélection du système de coordonnées, le modèle nécessite une plus grande capacité pour représenter des motifs initialement simples dans un système de coordonnées fixe ;
2) De nombreuses transformations de symétrie, telles que la translation, peuvent produire un nombre infini d'échantillons équivariants, ce qui rend difficile une amélioration limitée des données pour refléter pleinement la symétrie des données ;
3) Dans certains cas, il est nécessaire de construire un modèle très approfondi pour obtenir de bons résultats de prédiction. Si chaque couche du modèle ne peut pas maintenir l'équivariance, il sera difficile de prédire le résultat global de l'équivariance ;
4) Dans des problèmes scientifiques tels que la modélisation moléculaire, il est crucial de fournir une prédiction robuste aux transformations de symétrie afin que l'apprentissage automatique puisse être utilisé de manière fiable.
En raison des nombreuses lacunes de l’augmentation des données, de plus en plus de recherches se concentrent sur la conception de modèles d’apprentissage automatique répondant aux exigences de symétrie. Dans le cadre de l'architecture d'adaptation de symétrie, le modèle peut se concentrer sur la tâche de prédiction de cible d'apprentissage sans amélioration des données.
2.2 Equivariabilité sous transformation de symétrie discrète
Dans cette section, l'auteur fournit un exemple de maintien de l'équivariance sous des transformations de symétrie discrète dans un modèle d'IA. Cet exemple de problème simule la cartographie d'un champ de flux scalaire dans un plan 2D d'un instant à l'autre. Lorsque le champ de flux d'entrée pivote de 90, 180 et 270 degrés, le champ de flux de sortie pivote également en conséquence. Son expression mathématique est la suivante :
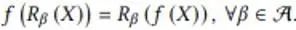
où f représente la fonction de mappage de champ de flux et R représente la transformation de rotation discrète. Cohen et al. ont proposé des réseaux neuronaux convolutifs de groupe équivariant (G-CNN) pour résoudre ce problème. Son composant de base le plus simple est la convolution ascendante :
1) Faites d'abord pivoter le noyau de convolution sous tous les angles dans la transformation symétrique, et utilisez le noyau de convolution tourné pour effectuer les opérations de convolution correspondantes sur l'entrée afin d'obtenir plusieurs couches de caractéristiques, et empilez ces couches de caractéristiques dans la dimension de rotation nouvellement générée α Ensemble 2 ; ) La mise en commun est effectuée dans cette dimension de rotation α, de sorte que la sortie résultante produira une rotation correspondante lorsque l'entrée X subit une rotation.
En raison de l'existence de l'opération de pooling, bien que les lignes équivariantes soient conservées, ces fonctionnalités ne peuvent pas transporter d'informations de direction. Habituellement, les G-CNN adoptent la structure illustrée dans la figure suivante :
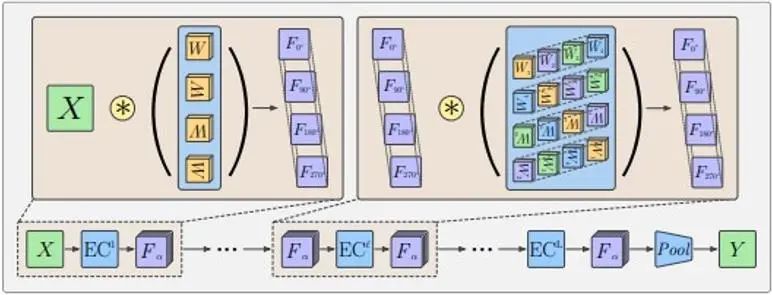
Tout d'abord, un noyau de convolution rotationnelle est utilisé pour augmenter la dimension de l'entrée, puis une couche de convolution de groupe multicouche est utilisée pour que chaque couche d'entités réponde aux exigences d'équivariance rotationnelle tout en conservant la dimension rotationnelle, et enfin une couche de pooling est utilisé pour éliminer la dimension de rotation. Cela permet à la couche d’entités intermédiaire de mieux détecter les modèles dans les positions et orientations relatives des entités. La signification de l'équivariance de la couche de caractéristiques intermédiaire est que la couche de caractéristiques tourne en conséquence sous la transformation de rotation, et l'ordre dans la dimension de rotation tourne également et la conception de rotation et de rotation du noyau de convolution dans la couche de convolution de groupe utilisée fait également ; la sortie La couche de fonctionnalités peut conserver cette caractéristique d'équivariance.
2.3-2.5 Construction d'un modèle équivariant de transformation continue 3D
Dans de nombreux problèmes scientifiques, nous nous concentrons sur les symétries de rotation et de translation continues dans l’espace 3D. Par exemple, lorsque la structure des molécules chimiques tourne et se déplace, le vecteur composé d’attributs moléculaires prédits subit les transformations correspondantes. Ces transformations de rotation continue R et les transformations de translation t constituent les éléments du groupe SE(3), et ces transformations peuvent être exprimées sous forme de matrices de transformation dans l'espace vectoriel. Les matrices de transformation dans différents espaces vectoriels peuvent être différentes, mais ces espaces vectoriels peuvent être décomposés en sous-espaces vectoriels indépendants. Il y a les mêmes règles de transformation dans chaque sous-espace, c'est-à-dire que le vecteur obtenu en appliquant tous les éléments de transformation du groupe au vecteur du sous-espace est toujours dans le sous-espace. Par conséquent, les éléments de transformation du groupe peuvent être irréductibles dans le. sous-espace. Représentation matricielle de transformation. Par exemple, les scalaires tels que l'énergie totale et l'écart énergétique restent inchangés sous l'action des éléments du groupe SE(3), et leur matrice de transformation est exprimée sous la forme D^0(R)=1 ; Vecteurs 3D tels que les champs de force La rotation correspondante se produit sous l'action, et sa matrice de transformation est exprimée par D^1(R)=R dans un espace vectoriel de dimension supérieure, D^l(R) est un 2l+1 ; -matrice carrée dimensionnelle. Ces matrices de transformation D^l(R) sont appelées matrice Wigner-D d'ordre l correspondant à la rotation R, et le sous-espace vectoriel correspondant devient le sous-espace invariant irréductible d'ordre l du groupe SE(3), et le Le vecteur qu'il contient est appelé l Vecteur équivariant d'ordre. Sous transformation par translation, ces vecteurs restent toujours inchangés, car les propriétés qui nous intéressent ne sont liées qu'à des positions relatives.
La manière habituelle de mapper des informations géométriques 3D sur des entités du sous-espace invariant du groupe SE(3) consiste à utiliser le mappage de fonctions harmoniques sphériques. La fonction harmonique sphérique Y^l mappe un vecteur tridimensionnel en un vecteur 2l+1 dimensionnel, qui représente le coefficient lorsque le vecteur d'entrée est décomposé en 2l+1 fonctions harmoniques sphériques de base. Comme le montre la figure ci-dessous, étant donné que seul un nombre limité de bases est utilisé, la fonction delta sur la sphère représentée par le vecteur tridimensionnel sera élargie dans une certaine mesure.

Les harmoniques sphériques ont les propriétés équivariantes suivantes :
Parmi eux, D est la matrice Wigner-D d’ordre l mentionnée précédemment. Par conséquent, une fonction spatiale est décomposée en une combinaison de vecteurs équivariants d’ordres différents sous transformation de rotation.
En supposant que dans un réseau neuronal graphique avec des coordonnées atomiques comme nœuds, la caractéristique du nœud h est un vecteur équivariant d'ordre l_1, alors le transfert et la mise à jour des informations graphiques suivantes peuvent garantir que le h mis à jour maintient également l'équivariance :
L’étape clé est l’opération de produit tensoriel (TP) lors du transfert d’informations. Parmi eux, vec signifie vectoriser la matrice, et le coefficient C est une matrice avec 2l_3+1 lignes (2l_1+1) (2l_2+1) colonnes.
La caractéristique du nœud h est un vecteur dans le sous-espace invariant irréductible d'ordre l_1. La fonction harmonique sphérique Y de la direction du bord r_ij est un vecteur dans le sous-espace invariant irréductible d'ordre l_2. l'espace est réductible, et le coefficient C est la relation de conversion de cet espace réductible en un sous-espace invariant irréductible d'ordre l_3. Par exemple, l’espace produit direct de deux vecteurs tridimensionnels est le suivant :
La matrice de transformation de rotation de l'espace produit direct peut être convertie en matrice diagonale à trois blocs au milieu de la figure ci-dessus, ce qui signifie que cet espace peut être décomposé en trois sous-espaces invariants irréductibles de dimensions 1, 3 et 5, c'est-à-dire 3⨂ Décomposition de l'espace vectoriel de 3=1⊕3⊕5. Le coefficient C est la matrice de transformation de cet espace à neuf dimensions vers ces espaces respectivement à 1 dimension, 3 dimensions et 5 dimensions. Dans la formule ci-dessus, l_1, l_2 et l_3 ne prennent tous qu'une seule valeur et sont des entités équivariantes d'ordre fixe. Les entités du réseau réel peuvent être une combinaison de ces différentes entités d'ordre.
2.6-2.7 Dans les exemples précédents, la théorie de la théorie des groupes et les propriétés des fonctions harmoniques sphériques ont été utilisées. Les connaissances de base de la théorie des groupes et des fonctions harmoniques sphériques sont présentées en détail dans ces deux chapitres de l'article.
2.8 Le noyau orientable constitue une forme générale de réseau équivariant
Les couches de réseau équivariantes précédentes sous transformations discrètes et continues peuvent être décrites sous la forme d'une convolution variable unifiée (CNN orientable) :
Parmi eux, x et y sont des coordonnées spatiales, f_in(y) représente le vecteur de fonctionnalités d'entrée à la coordonnée y, f_out(x) représente le vecteur de fonctionnalités de sortie à la coordonnée x et K est la transformation de l'espace de fonctionnalités d'entrée en entité de sortie. espace. L'opération de convolution garantit l'équivariance translationnelle Afin d'assurer l'équivariance sous d'autres transformations spatiales affines, le noyau de convolution K doit également satisfaire les contraintes de symétrie suivantes :
Parmi eux, g est la transformation dans le groupe de transformation spatiale, et ρ_in et ρ_out représentent respectivement la représentation de la transformation dans les espaces de fonctionnalités d'entrée et de sortie (c'est-à-dire la matrice de transformation).
À ce stade, l’explication théorique de la symétrie et de l’équivariance donnée dans l’article est pratiquement terminée, suivie d’un aperçu séparé des multiples domaines répertoriés dans le chapitre 1.
les références
[1] Ren P, Rao C, Liu Y et al. PhyCRNet : réseau convolutionnel-récurrent informé par la physique pour résoudre les PDE spatio-temporelles [J]. Méthodes informatiques en mécanique appliquée et ingénierie, 2022, 389 : 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
[1] Xuan Zhang, Limei Wang, Jacob Helwig et al. 2023. Intelligence artificielle pour la science dans les systèmes quantiques, atomiques et continus. arXiv : https://arxiv.org/abs/2307.08423
【2】 Taco Cohen et Max Welling. 2016. Réseaux convolutifs équivariants de groupe. Lors de la Conférence internationale sur l'apprentissage automatique. PMLR, 48 : 2990-2999.
【3】 Nathaniel Thomas, Tess Smidt, Steven Kearnes et al. 2018. Réseaux de champs tensoriels : réseaux neuronaux équivariants de rotation et de translation pour les nuages de points 3D. arXiv : https://arxiv.org/abs/1802.08219
Maurice Weiler, Mario Geiger, Max Welling et al. 2018. CNN orientables 3D : apprentissage de fonctionnalités équivariantes en rotation dans les données volumétriques. Dans Progrès des systèmes de traitement de l'information neuronale
Un programmeur né dans les années 1990 a développé un logiciel de portage vidéo et en a réalisé plus de 7 millions en moins d'un an. La fin a été très éprouvante ! Google a confirmé les licenciements, impliquant la « malédiction des 35 ans » des codeurs chinois des équipes Flutter, Dart et . Python Arc Browser pour Windows 1.0 en 3 mois officiellement la part de marché de GA Windows 10 atteint 70 %, Windows 11 GitHub continue de décliner l'outil de développement natif d'IA GitHub Copilot Workspace JAVA. est la seule requête de type fort capable de gérer OLTP+OLAP. C'est le meilleur ORM. Nous nous rencontrons trop tard.