Conférence de dissertation | État du réseau tenseur isométrique bidimensionnel d'informatique quantique

L'équipe de la communauté open source chinoise a réalisé sa première diffusion en direct, racontant l'histoire de la communauté open source chinoise au nom du partage.

Partageur : Wu Shaojun ｜École** : Université des sciences et technologies électroniques de Chine**

courte introduction

Surmonter la croissance exponentielle de la complexité lors de la simulation de systèmes quantiques à N corps est un objectif ambitieux en physique. Actuellement, pour les propriétés de l’état fondamental des systèmes quantiques unidimensionnels, les méthodes basées sur les états de réseaux tensoriels (TNS) constituent un moyen efficace de fournir des solutions numériques fondamentalement précises. Dans les systèmes bidimensionnels, certains progrès ont également été réalisés grâce à l'introduction d'algorithmes permettant d'optimiser le TNS pour divers modèles de réseau. Cette fois, nous présenterons une nouvelle méthode de représentation de l'état quantique, à savoir le TNS isométrique, qui peut être utilisée pour décrire l'état quantique d'un système bidimensionnel et présente des avantages informatiques. De plus, nous présenterons également comment utiliser des mesures locales pour. reconstruire l'état quantique. Une méthode pour construire MPS, qui n'a qu'un nombre linéaire d'opérations.

Documents connexes 1

**Titre : États de réseau tensoriel isométrique en deux dimensions
Auteur : Michael P. Zaletel et Frank Pollmann
Journal : **Phys Rev. Lett.

**Date de publication :** 24 janvier 2020

Documents connexes 2

**Crédit : Tomographie d'état quantique efficace
Crédits : Marcus Cramer, Martin B. Plenio, Steven T. Flammia, Rolando Somma, David Gross, Stephen D. Bartlett, Olivier Landon-Cardinal, David Poulin et Yi-Kai Liu
:** Nature Communications 1, 149 (2010)

**Publié :** 21 décembre 2010

** introduction
**

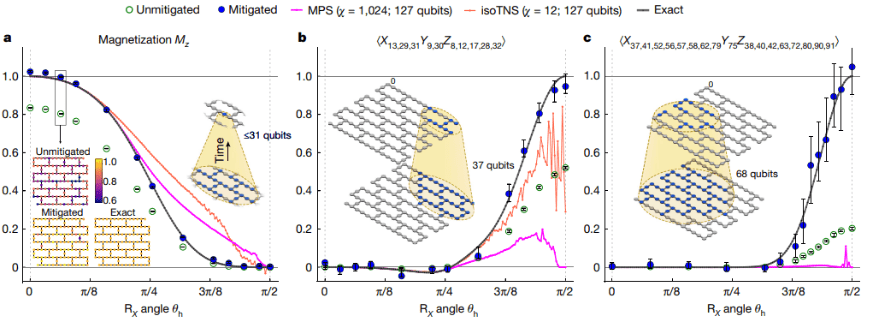
(Source de l'image : Nature volume 618, pages 500 à 505 (2023))

Récemment, IBM a implémenté la simulation du modèle d'Ising à champ transversal bidimensionnel sur 127 processeurs quantiques. À titre de comparaison, des simulations classiques doivent être utilisées pour obtenir des résultats précis. Ce travail utilise des observations de poids 1, de poids 10 et de poids 17 pour mesurer le circuit quantique du trotteur en 5 étapes, et les résultats expérimentaux sont présentés dans la figure.

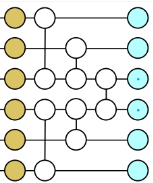
Lors de la réalisation de simulations classiques afin d'obtenir des solutions précises, la méthode du cône de lumière et de la profondeur réduite (LCDR) est utilisée ici. Il est divisé en deux parties. L'une consiste à réduire le nombre de couches de circuits qui doivent être simulées à travers les caractéristiques entre les portes quantiques ; l'autre partie consiste à considérer que les qubits liés à la quantité d'observation A sont locaux, ce qui signifie que seule une partie des qubits doit être prise en compte. Evolution peut alors calculer le résultat de l'observation finale au lieu des 127 bits. Les nombres de qubits associés aux observations de poids 1, de poids 10 et de poids 17 sont respectivement 31, 37 et 68. Il convient de noter que la simulation avec 68 qubits dépasse encore les capacités des simulations par force brute par les ordinateurs classiques. Par conséquent, ce travail introduit les réseaux tensoriels, les états de produits matriciels 1D (MPS) et les états de réseaux tenseurs isométriques 2D (iso TNS), pour la simulation.

** Introduction à l'état du produit matriciel (MPS)
**

1. Connaissance de base des tenseurs

(1) Définition et représentation graphique

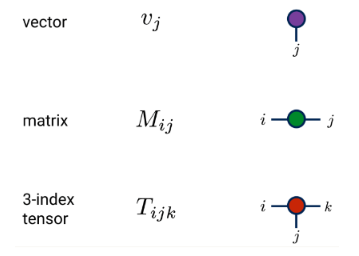
(2) Rétrécissement du même indicateur

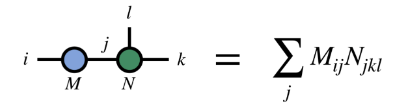
2、MPS

Pour un système unidimensionnel avec N points de grille, si chaque point de grille a d états quantiques, l'espace de Hilbert multi-corps peut être exprimé comme le produit tensoriel de l'espace de Hilbert de la grille :

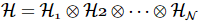
Les postures multiples arbitraires correspondantes peuvent être exprimées comme suit :

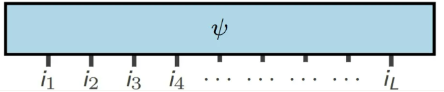
(Source de l'image : arXir : 1603.03039, 2016)

L'idée principale de l'état du produit matriciel (MPS) est d'exprimer l'état multi-corps comme suit :

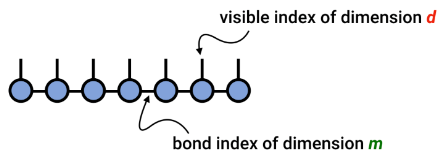
(Source de l'image : arXir : 1603.03039, 2016)

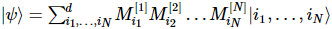
Chaque unité est un tenseur du troisième ordre, dans lequel l'indice physique est l'état quantique du point de grille, et l'indice auxiliaire peut être considéré comme l'intrication quantique entre lui et les systèmes gauche et droit.

Décomposition SVD :

Pour une 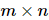matrice complexe générale A, il existe une décomposition telle que 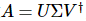, où

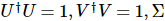est une 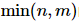matrice diagonale de dimension , et les éléments sur la diagonale sont appelés valeurs singulières. De manière générale, les valeurs singulières sont classées de la plus grande à la plus petite le long de la diagonale.

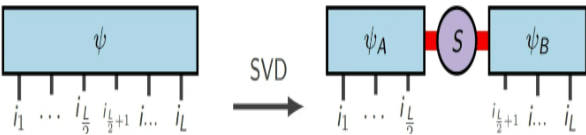
(Source de l'image : arXir : 1603.03039, 2016)

Où S représente une valeur singulière. Si l'intrication entre les deux parties du système n'est pas forte, le spectre des valeurs singulières a tendance à se dégrader rapidement, et seulement moins de valeurs singulières doivent être conservées pour conserver la plupart des informations de la matrice. Supposons que nous stipulions que chaque groupe de décompositions de Schmidt ne conserve pas plus de m valeurs singulières. En fin de compte, nous n'avons besoin que 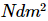d'un nombre réel pour représenter approximativement cet état à plusieurs corps. Par rapport à la méthode de représentation originale qui nécessite 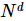1 paramètre, cette représentation a une complexité spatiale linéaire pour le nombre de points de grille, et l'efficacité est bien supérieure à la complexité de croissance exponentielle de la représentation du produit tensoriel d'origine.

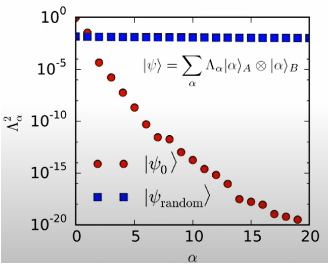
(Source de l'image : arXir : 1603.03039, 2016)

Le processus pour obtenir MPS :

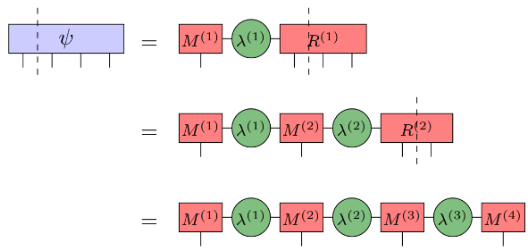
(Source de l'image : arXir : 1603.03039, 2016)

PARCE QUE:

Pour un opérateur à plusieurs corps, comme les états, nous pouvons écrire l'opérateur à plusieurs corps sous forme de produit matriciel (MPO) :

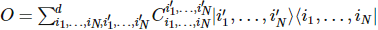
A la différence des états, l’hamiltonien composé d’opérateurs locaux peut naturellement s’écrire sous forme de produits matriciels :

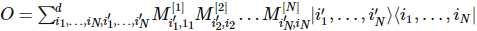
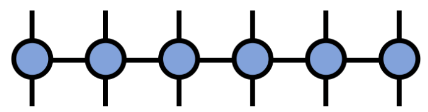
(Source de l'image : arXir : 1603.03039, 2016)

L'opérateur de produit matriciel conserve toujours la structure du produit matriciel après avoir agi sur l'état du produit matriciel :

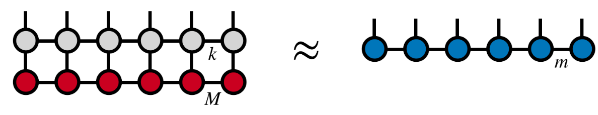
(Source de l'image : arXir : 1603.03039, 2016)

États du réseau tenseur isométrique en deux dimensions

1. Résumé

Les états des réseaux tensoriels constituent un outil prometteur mais numériquement difficile pour les problèmes quantiques bidimensionnels à N corps. Dans cet article, les auteurs introduisent l'ansatz TNS isométriquement restreint, une forme qui permet un rétrécissement efficace des réseaux tensoriels. Afin de comparer numériquement ansatz, les auteurs ont d'abord démontré que la représentation MPS de l'état fondamental du modèle d'Ising à champ transversal bidimensionnel peut être efficacement convertie en isoTNS. En fait, les auteurs ont implémenté un algorithme TEBD 2D et ont montré qu'il était efficace. trouve la forme isoTNS Approximation de l'état fondamental du modèle 2D.

2. État du réseau tenseur isométrique

1) Condition d'isométrie : pour une 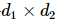matrice dimensionnelle M, ou

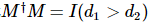. Dans les diagrammes tensoriels, les flèches sont généralement utilisées pour indiquer l'orthogonalité, qui stipule que la matrice unitaire est obtenue en rétrécissant l'indice vers l'intérieur du tenseur et son tenseur conjugué.

2) Forme canonique de MPS :

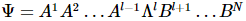
Parmi eux, A et B satisfont aux conditions orthogonales gauche et droite. La condition orthogonale gauche signifie que 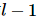la contraction du quantum précédent et sa propre transposition est une matrice unitaire, et la condition orthogonale droite signifie que 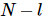la contraction du quantum suivant et sa propre transposition est une matrice unitaire, 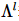représentant un élément diagonal décroissant. la matrice diagonale est également appelée centre orthogonal.

3) La valeur attendue de l'opération locale peut être directement 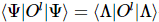obtenue par, car son tenseur AB externe se rétrécit à 1 selon la condition d'isométrie.

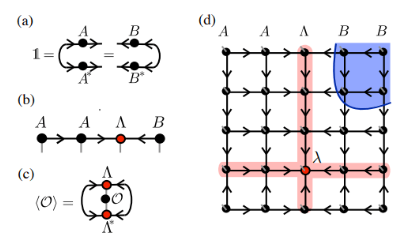
(Source de l'image : Phys. Rev. Lett. 124, 037201)

Généralisez à deux dimensions :

Par analogie avec la formule ci-dessus, nous exigeons que chaque ligne et colonne de TNS soit une isométrie. Cette contrainte peut être en outre exigée en exigeant que chaque tenseur soit une isométrie. Comme le montre la figure d ci-dessus, la partie rouge n'a que des flèches vers l'intérieur. Il s'agit donc de « l'hypersurface orthogonale » unidimensionnelle de TNS, 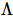qui est la fonction d'onde sous la base orthonormée standard. 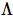Elle peut donc être traitée comme MPS et. peut être lui-même mis sous une forme canonique unidimensionnelle (son centre orthogonal peut être déplacé librement à l'aide de l'algorithme canonique unidimensionnel). Pour tout opérateur , il existe 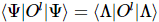, c'est-à-dire une réduction de dimensionnalité de la valeur attendue unidimensionnelle qui peut être calculée efficacement par l'algorithme MPS standard sans autre approximation. Ceci contraste fortement avec le TNS général, où la valeur attendue nécessite l'utilisation d'un rétrécissement approximatif de l'ensemble du réseau.

3. Hypersurface orthogonale en mouvement

La forme orthogonale centrale n'est utile en termes de calcul que si l'hypersurface orthogonale Lammda peut être déplacée efficacement à travers le réseau. En une dimension, on peut réaliser le mouvement du centre orthogonal grâce à la décomposition (QR ou SVD) de n'importe quelle matrice orthogonale. En deux dimensions, il faut également déplacer toute la colonne. Mais pour les systèmes bidimensionnels, la méthode de décomposition matricielle orthogonale n'est pas valide car elle détruit la localité requise pour être exprimée en MPS.

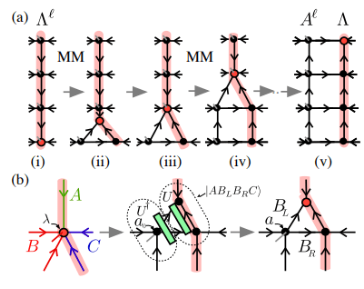
(Source de l'image : Phys. Rev. Lett. 124, 037201)

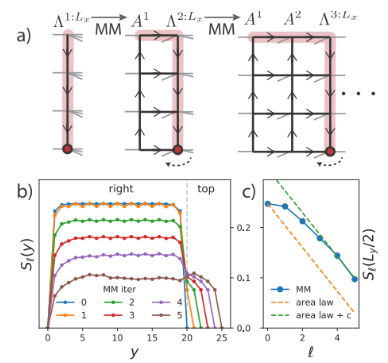
Dans cet article, l'auteur utilise la méthode Moses Move pour déplacer le centre de la surface orthogonale. Comme le montre la figure ci-dessus, après l'algorithme MM, l'hypersurface orthogonale est divisée en produit des 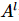états orthogonaux gauche et colonne zéro sans indicateurs physiques 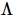. Parmi eux, la décompression est réalisée en appliquant continuellement le processus de « fractionnement » illustré à la figure (b). L'index du point central 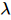est regroupé en trois états 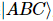et « divisé » en trois tenseurs en deux étapes.

4. MPS étendu à isoNTS

(Source de l'image : Phys. Rev. Lett. 124, 037201)

Étant donné une 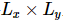fonction d'onde de l'état fondamental 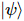, les auteurs ont proposé un algorithme itératif qui peut être 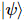intégré à l'isoTNS et 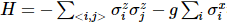ont testé le modèle de champ transversal sing. Considérons une 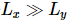bande et utilisez DMRG pour obtenir 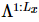l'état fondamental d'un MPS 1D, où chaque « site » contient la rangée de 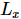spins correspondante [Figure (a)]. Comme le montre le 3ème panneau de la figure a, MM peut ensuite être utilisé pour « diviser » de manière itérative les colonnes de la fonction d'onde 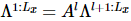, produisant ainsi de l'isoTNS. Dans cet exemple, la dimension de liaison est sélectionnée à 6. Lorsque g = 3,5 (phase paramagnétique), l'erreur sur chaque site 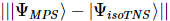est de 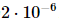. Dans ce cas, 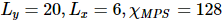. Les résultats sont présentés sur la figure b, qui montre que l'entropie d'intrication de la segmentation le long de l'hypersurface orthogonale diminue à mesure que le nombre d'itérations augmente. La figure c montre qu'à mesure que le nombre d'itérations augmente, l'entropie d'intrication décroît linéairement, ce qui est conforme aux attentes.

5. 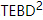Algorithme

(Source de l'image : Phys. Rev. Lett. 124, 037201)

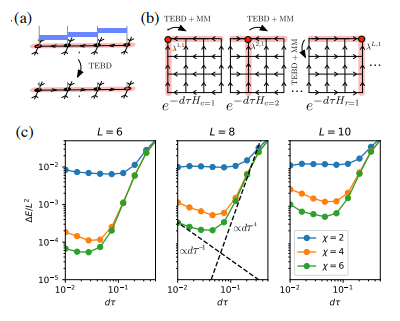
L'auteur a également implémenté 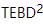l'algorithme. L'idée principale de TEBD est d'utiliser l'algorithme de recuit basé sur la décomposition de Trotter-Suzuki pour faire évoluer l'état MPS initialisé de manière aléatoire vers l'état fondamental, convertir le processus d'évolution en un problème de rétrécissement du réseau tensoriel et utilisez l'algorithme TEBD pour résoudre le retrait. Plus précisément, un pas à pas temporel trotterisé est proposé pour isoTNS, qui peut obtenir l'état fondamental grâce à une évolution temporelle virtuelle. En supposant qu'il n'y a qu'une interaction avec le voisin le plus proche, nous divisons l'hamiltonien en termes agissant sur les colonnes et les lignes 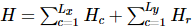, puis effectuons Trotterized 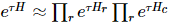, comme le montre la figure (a). Pour les mises à jour 1D TEBD, 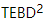il peut être facilement amélioré au second ordre. Nous 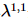partons du centre orthogonal, puis déplaçons progressivement le centre orthogonal en appelant l'algorithme 1D TEBD standard et l'algorithme MM. Dans une analyse, l'algorithme est en fait deux versions imbriquées de 1D TEBD, d'où le nom 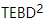. Parmi eux, 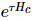l'évolution de est réalisée en appelant 1D TEBD, et sa complexité 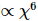est MM , tandis que la complexité complète de mise à jour du PEPS sans contrainte est 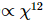. La figure (c) montre la densité d'erreur d'énergie du modèle d'Ising à champ transversal g = 3, 5 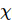en fonction de la taille du pas de Trotter pour différentes tailles de système et dimensions maximales de liaison 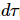. À mesure que la taille de la liaison 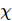augmente, l’énergie minimale converge vers le résultat exact.

Tomographie d'état quantique efficace

1. Résumé

Déduire des états quantiques à partir de données mesurées devient impossible pour les systèmes plus grands, car le nombre de mesures et la quantité de calculs nécessaires pour les traiter augmentent de façon exponentielle avec la taille du système. Dans cet article, un schéma de tomographie est proposé, plus avantageux que la tomographie directe de la taille du système. Cette méthode nécessite une manipulation uniforme d’un nombre constant de sous-systèmes et repose uniquement sur un nombre linéaire de manipulations expérimentales. Ce schéma peut être appliqué à un large éventail d’états quantiques, notamment les MPS.

2. Schéma basé sur la transformation unitaire

L'idée centrale de cette méthode est de trouver une séquence d'opérations pour démêler une chaîne de gauche à droite. Chaque opération de cette séquence est locale et indépendante de la dimension N.

Supposons que l’état idéal soit 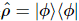, et nous supposons que cet état quantique est un MPS avec une dimension de liaison donnée de R. Le but de cette méthode est de reconstruire cela .

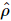Processus d'algorithme :

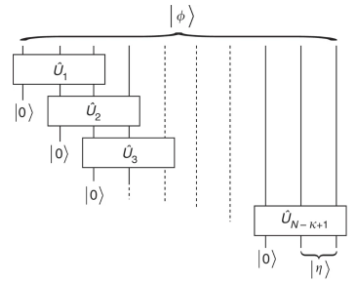
(Source de l'image : Nature Communications 1, 149 (2010))

1) Tout d'abord, nous prenons 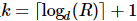, puis effectuons une tomographie d'état quantique standard sur les k premiers sites, puis la matrice de densité réduite des k premiers sites est : 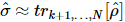, cette matrice de densité réduite a une décomposition propre 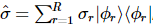, où, 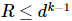. Par conséquent, il existe une matrice de densité avec un qudit en moins dont le rang R et la somme des valeurs propres 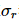sont 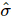les mêmes.

2). Ensuite, nous utilisons davantage 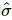les informations pour construire une matrice unitaire pour les k premières positions 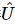, qui 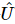peut démêler le premier site.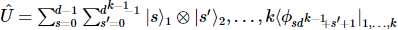

3) Appliquez 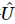l'action à l'état d'origine pour obtenir : 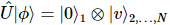Parmi eux, 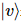il y a des 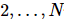états purs en position.

4). Répétez ensuite le processus ci-dessus pour les 2ème positions suivantes à k+1. Par analogie, nous pouvons obtenir une séquence de matrices unitaires 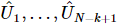, dont chacune 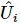agit à 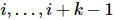des positions. Cette séquence devient 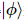, 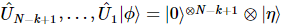où chacun 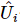agit dans 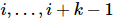des positions. Cette séquence fait que 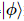, 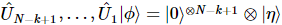où , 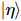sont des états purs aux k-1 dernières positions.

En résumé, ce schéma déduit un circuit quantique pour préparer le MPS. La décomposition MPS peut être facilement obtenue par 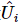et .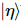

3. Erreur
L'erreur de cette méthode provient principalement de deux aspects. L'un est l'incapacité d'exprimer pleinement l'état quantique en raison de la limitation de la dimension de la liaison, et l'autre est l'erreur causée par la mesure.

Étant donné une matrice unitaire démêlée estimée 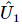, un état arbitraire 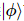peut être exprimé comme suit : 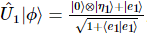, où 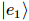est le vecteur d'erreur.

Dans les étapes suivantes, nous pouvons obtenir l'état sous la forme suivante : 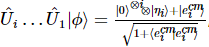, où,

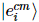est l’erreur cumulée.

Nous pouvons tronquer ce vecteur d'erreur en mesurant les i premières particules dans la base standard et en post-sélectionnant le résultat de tous les zéros. La probabilité que cela se produise est d'environ 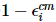, et laisse le système dans cet état .

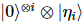Après une série de transformations unitaires, l’état final est :

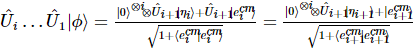
Parmi eux, 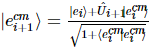donc, .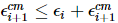

Nous pouvons constater que l'erreur s'accumule linéairement avec le nombre de particules, et le MPS que nous obtenons est enregistré comme : 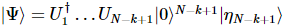, alors nous avons :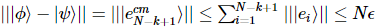

dans, 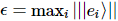. L'erreur globale est au maximum la somme des erreurs individuelles à chaque étape.

Conférence de dissertation | État du réseau tenseur isométrique bidimensionnel d'informatique quantique

Je suppose que tu aimes