1.はじめに
1ホップフィールドニューラルネットワーク
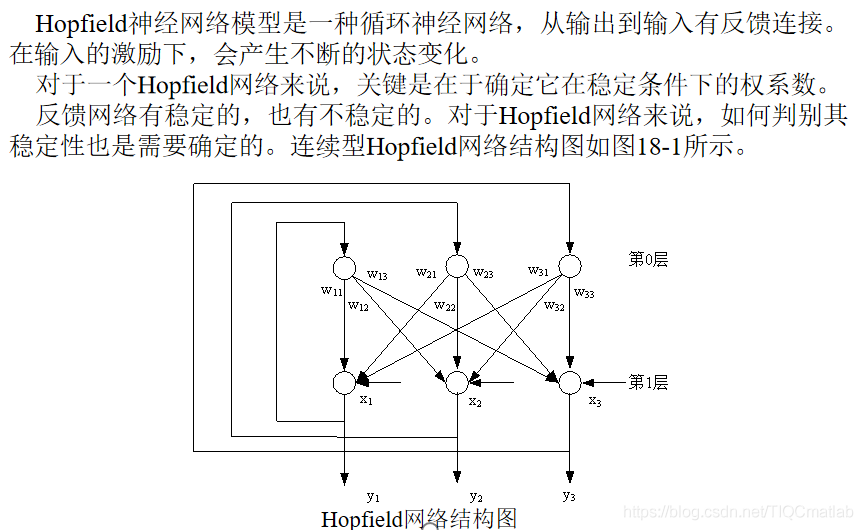
2離散ホップフィールドネットワーク

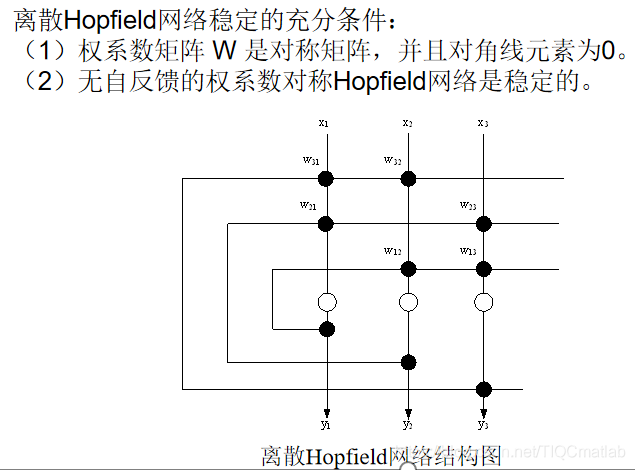
3連続ホップフィールドネットワーク
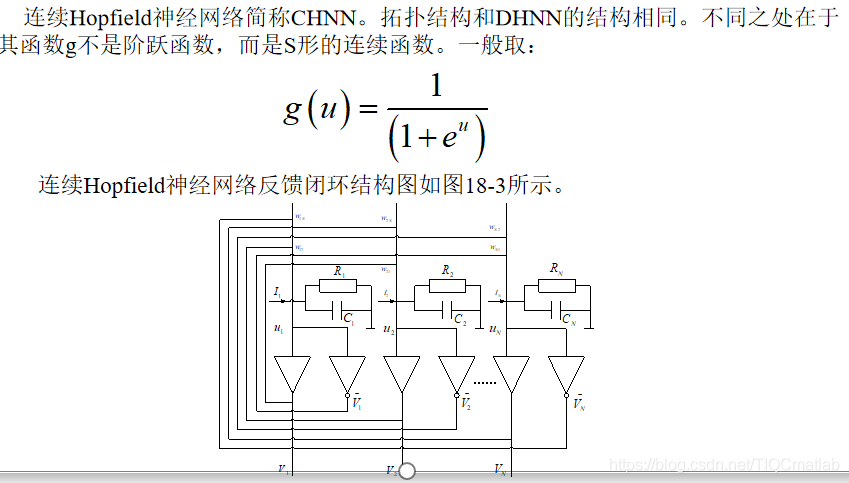
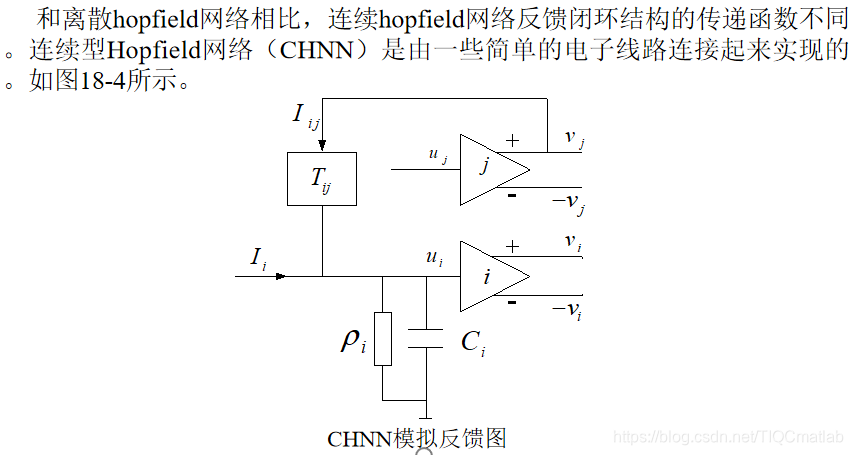
CHNNは、非線形微分方程式で記述されます。ネットワークの安定性は、エネルギー関数(Lyapunov関数とも呼ばれます)を構築し、Lyapunovの2番目の安定性定理を使用して判断します。
説明:
(1)リアプノフ関数が一意ではない;
(2)ネットワークのリアプノフ関数が見つからない場合、ネットワークが不安定であると証明できない;
(3)現在統一されたリアプノフ検索関数法がない;
(4 )ネットワークの安定性を研究するためにエネルギー関数法を使用することは、数学的に厳密ではありません。
最適化問題の目的関数がネットワークのエネルギー関数に変換され、問題の変数がネットワークの状態に対応している場合、ホップフィールドニューラルネットワークを使用して最適化の組み合わせ問題を解くことができます。
最適化計算の問題を解決するためにホップフィールドニューラルネットワークを適用するための一般的な手順は次のとおりです。
(1)問題の分析:ネットワーク出力は問題の解決に対応します。
(2)ネットワークエネルギー関数を構築します。最小値を最適に対応させます。問題の解決策;
(3)ネットワーク構造の設計:動的方程式を取得するためのエネルギー関数とネットワーク安定性条件からネットワークパラメーターを設計します;
(4)MATLABソフトウェアシミュレーション。
第二に、ソースコード
%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function main
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
global A D
%% 导入城市位置
load city_location
%% 计算相互城市间距离
distance=dist(citys,citys');
%% 初始化网络
N=size(citys,1);
A=200;
D=100;
U0=0.1;
step=0.0001;
delta=2*rand(N,N)-1;
U=U0*log(N-1)+delta;
V=(1+tansig(U/U0))/2;
iter_num=10000;
E=zeros(1,iter_num);
%% 寻优迭代
for k=1:iter_num
% 动态方程计算
dU=diff_u(V,distance);
% 输入神经元状态更新
U=U+dU*step;
% 输出神经元状态更新
V=(1+tansig(U/U0))/2;
% 能量函数计算
e=energy(V,distance);
E(k)=e;
end
%% 判断路径有效性
[rows,cols]=size(V);
V1=zeros(rows,cols);
[V_max,V_ind]=max(V);
for j=1:cols
V1(V_ind(j),j)=1;
end
C=sum(V1,1);
R=sum(V1,2);
flag=isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%% 结果显示
if flag==1
% 计算初始路径长度
sort_rand=randperm(N);
citys_rand=citys(sort_rand,:);
Length_init=dist(citys_rand(1,:),citys_rand(end,:)');
for i=2:size(citys_rand,1)
Length_init=Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
end
% 绘制初始路径
figure(1)
plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
for i=1:length(citys)
text(citys(i,1),citys(i,2),[' ' num2str(i)])
end
text(citys_rand(1,1),citys_rand(1,2),[' 起点' ])
text(citys_rand(end,1),citys_rand(end,2),[' 终点' ])
title(['优化前路径(长度:' num2str(Length_init) ')'])
axis([0 1 0 1])
grid on
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
% 计算最优路径长度
[V1_max,V1_ind]=max(V1);
citys_end=citys(V1_ind,:);
Length_end=dist(citys_end(1,:),citys_end(end,:)');
for i=2:size(citys_end,1)
Length_end=Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
end
disp('最优路径矩阵');V1
% 绘制最优路径
figure(2)
plot([citys_end(:,1);citys_end(1,1)],...
[citys_end(:,2);citys_end(1,2)],'o-')
for i=1:length(citys)
text(citys(i,1),citys(i,2),[' ' num2str(i)])
end
text(citys_end(1,1),citys_end(1,2),[' 起点' ])
text(citys_end(end,1),citys_end(end,2),[' 终点' ])
title(['优化后路径(长度:' num2str(Length_end) ')'])
axis([0 1 0 1])
grid on
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
% 绘制能量函数变化曲线
figure(3)
plot(1:iter_num,E);
ylim([0 2000])
title(['能量函数变化曲线(最优能量:' num2str(E(end)) ')']);
xlabel('迭代次数');
ylabel('能量函数');
else
disp('寻优路径无效');
end
%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function TSP_hopfield()
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
% step 1
A=1.5;
D=1;
u0=0.02;
step=0.01;
% step 2
N=8;
DistanceCity=dist(citys,citys');
% step 3
u=2*rand(N,N)-1;
U=0.5*u0*log(N-1)+u;
V=(1+tanh(U/u0))/2;
end
3、実行中の結果


四、備考
完全なコードまたは書き込み追加QQ1564658423過去のレビュー
>>>>>>
[予測モデル] matlab粒子群に基づくlssvm予測[Matlabソースコード103を含む]
[lSSVM予測] matlabクジラ最適化アルゴリズムに基づくlSSVMデータ予測[Matlabソースコードを含む104]
[lstm予測] matlabクジラ最適化アルゴリズムに基づく改善されたlstm予測[Matlabソースコード105を含む]
[SVM予測] matlabバットアルゴリズムに基づく改善されたSVM予測(1)[Matlabソースコード106を含む]
[ SVM予測]に基づくmatlabBP
ニューラルネットワーク予測に基づくsvmサポートベクターマシン予測[Matlabソースコード107を含む] [予測モデル] [Matlabソースコード108を含む]
[lssvm予測モデル]を最適化するmatlabグレイウルフアルゴリズムバットアルゴリズムに基づく改善された最小二乗サポートベクターマシンlssvm予測[Matlab109の問題]
[lssvm予測]サポートベクターマシンlssvm予測の蛾消火アルゴリズムに基づく改善[Matlab110]
[SVM予測] matlabバットアルゴリズムに基づくSVM予測の改善(2)[Matlabソースコード141を含む限目]
[Lssvm予測]改善された最小二乗サポートベクトルマシンMatlab蛾消火アルゴリズムに基づくlssvm予測[Matlabソースコード142を含む]
[ANN予測モデル] MATlab差分アルゴリズムに基づいてANNネットワーク予測を改善[Matlabソースコード151を含む]
[予測モデル] matlabRBFニューラルネットワーク予測モデルに基づく[Matlabソースコード177期間を含む]
[予測モデル] matlabSVM回帰予測アルゴリズムに基づく在庫傾向を予測する[Matlabソースコード180期間を含む]
[予測モデル] matlabBPニューラルに基づくネットワークモデル最適化予測[Matlabソースコード221を含む]
[予測モデル] matlabRLSアルゴリズムに基づくデータ予測[Matlabソースコード222を含む]
[予測モデル] matlab炭素排出制約に基づく石炭消費の最適予測[Matlabソースコード223を含む]