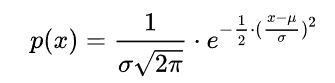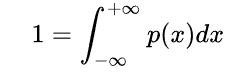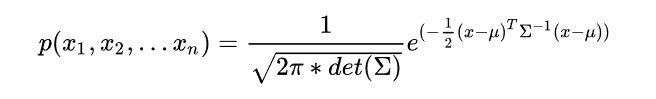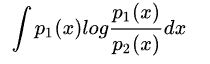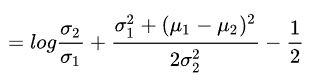深度学習/マシンの基本的な算術知識仕上げ学習（VIII）：中心極限定理、単変量および多変量ガウス分布

中心極限定理

ランダム変数X1、X2、... Xnを、独立同一分布し、限ら数学的期待値と分散を持っています： $E（X_I）= \ミュー$、 $D（X_I）= \シグマ^ 2$、その後、任意の実数xに対して、分布関数

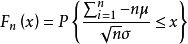
を満たす

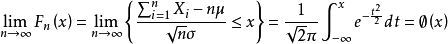
大nは、確率変数がこの定理、

約標準正規分布N（0,1）に従います。このように、大きなN、

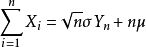
ほぼ正規分布 $N（nμ、nσ2）$。中心極限定理の定理は限り、実務において、最も単純で最も一般的な形態であり、nは十分に大きいが、それらが独立同一確率変数を分散し、通常変数とすることができるです。この方法は、大量のサンプルを扱うときに使用される数理統計学では非常に一般的ですが、それは重要なツールです。

中心極限定理の簡単なアプリケーション

参考文献[1]

ガウス分布

あまりにも分布正規分布であるものとして知られているガウス分布のガウス分布は、数学で非常に重要である、そのような確率分布として、物理学や工学分野、統計の多くの側面に大きな影響を与えています。

一つの元ガウス分布

ガウス分布の確率変数準拠している場合 $X \ simのN（\ムー、\シグマ^ 2）$，则有如下的概率密度函数

满足

而如果我们对随机变量 $X$进行标准化 $Z = \frac{X-\mu}{\sigma }$, 那么变量 $Z$服从0均值，1方程的一元标准高斯分布。

多元高斯分布

多维高斯分布的公式：

其中 $x=(x_1,x_2,...,x_n)$为一个n维向量， $\mu$是均值向量， $\sum$是协方差矩阵。

多元高斯分布的的线性变换

两个高斯分布的KL散度

参考资料[5]

两个一元（一维）高斯分布的KL散度 $KL(p_1||p_2)$：

KLダイバージェンス2多次元ガウス分布 $KL（P_1 || P_2）$：

このアルゴリズムは、我々はVAE時間を見れば見ることができ、それを記録、VAEに使用されます。

参考資料

[1] 中心極限定理、Baiduの百科事典
[2] https://zhuanlan.zhihu.com/p/38501770
[3] https://zhuanlan.zhihu.com/p/58987388
HTTPS [4]：// zhuanlan。 zhihu.com/p/90272131
[5] VAEの（1） - KLから出発