[TSP] MATLAB 파티클 스웜 알고리즘 Hopfield 기반 TSP 솔루션 [Matlab 소스 코드 224 포함]

1. 소개

1 Hopfield 신경망

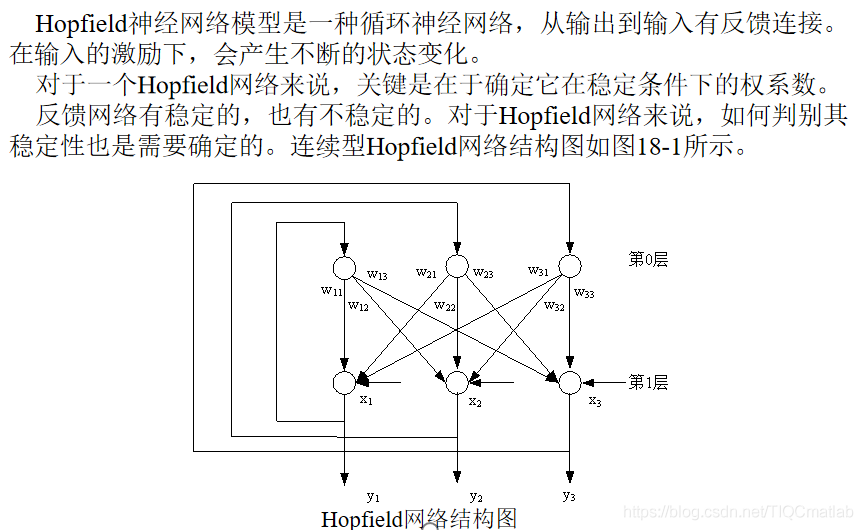
2 Discrete Hopfield 네트워크


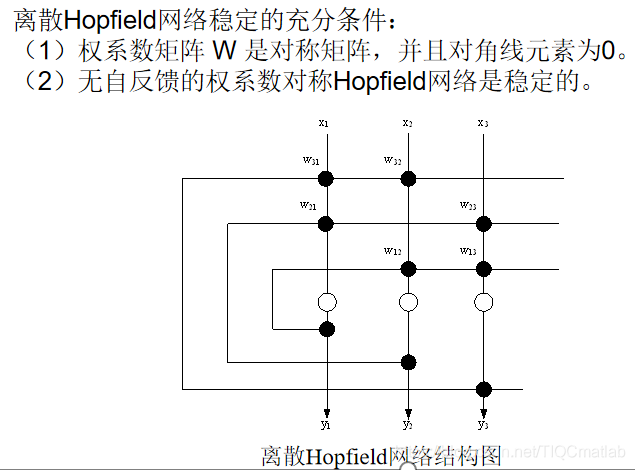
3 연속 Hopfield 네트워크


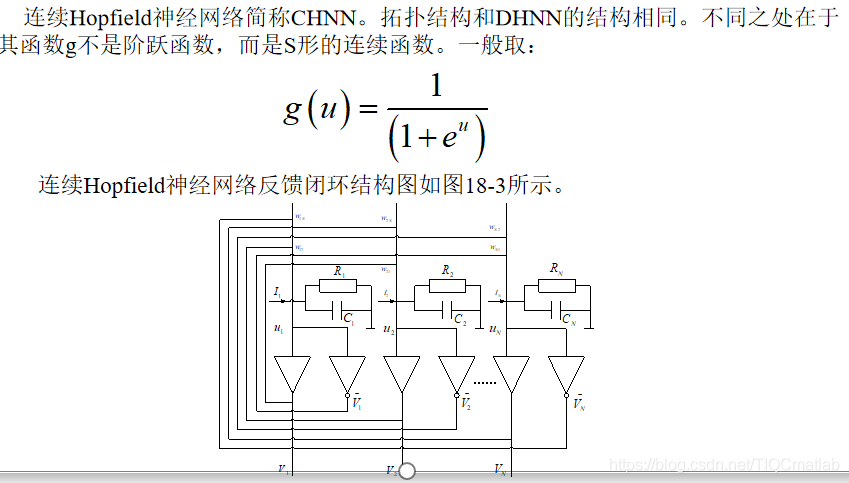
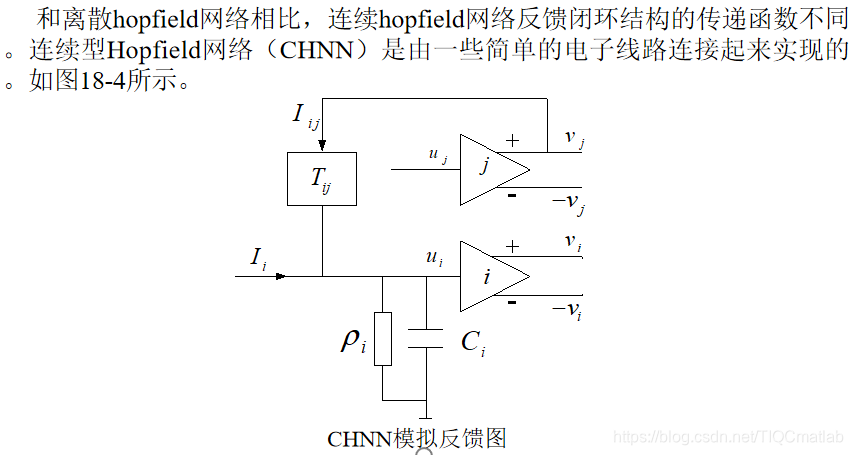
CHNN은 비선형 미분 방정식으로 설명됩니다. 네트워크의 안정성은 에너지 함수 (Lyapunov 함수라고도 함)를 구성하고 Lyapunov 2 차 안정성 정리를 사용하여 설명합니다.
설명 :
(1) Lyapunov 기능이 고유하지 않습니다.
(2) 네트워크의 Lyapunov 기능을 찾을 수없는 경우 네트워크가 불안정한 것으로 입증 될 수 없습니다.
(3) 현재 통합 된 Lyapunov 검색 기능 방법이 없습니다.
(4 ) 에너지 함수 방법을 사용하여 네트워크의 안정성을 연구하는 것은 수학적으로 엄격하지 않습니다.
최적화 문제의 목적 함수가 네트워크의 에너지 함수로 변환되고 문제의 변수가 네트워크의 상태에 해당하면 Hopfield 신경망을 사용하여 최적화 조합 문제를 해결할 수 있습니다.
최적화 계산 문제를 해결하기 위해 Hopfield 신경망을 적용하는 일반적인 단계는 다음과 같습니다.
(1) 문제 분석 : 네트워크 출력이 문제의 솔루션에 해당합니다.
(2) 네트워크 에너지 함수 구성 : 최적에 해당하는 최소값을 만듭니다. 문제의 해결책,
(3) 네트워크 구조 설계 : 에너지 함수 및 네트워크 안정성 조건에서 네트워크 매개 변수를 설계하여 동적 방정식을 얻습니다.
(4) MATLAB 소프트웨어 시뮬레이션.

둘째, 소스 코드

%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function main
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
global A D
%% 导入城市位置
load city_location
%% 计算相互城市间距离
distance=dist(citys,citys');
%% 初始化网络
N=size(citys,1);
A=200;
D=100;
U0=0.1;
step=0.0001;
delta=2*rand(N,N)-1;
U=U0*log(N-1)+delta;
V=(1+tansig(U/U0))/2;
iter_num=10000;
E=zeros(1,iter_num);
%% 寻优迭代
for k=1:iter_num  
    % 动态方程计算
    dU=diff_u(V,distance);
    % 输入神经元状态更新
    U=U+dU*step;
    % 输出神经元状态更新
    V=(1+tansig(U/U0))/2;
    % 能量函数计算
    e=energy(V,distance);
    E(k)=e;  
end
 %% 判断路径有效性
[rows,cols]=size(V);
V1=zeros(rows,cols);
[V_max,V_ind]=max(V);
for j=1:cols
    V1(V_ind(j),j)=1;
end
C=sum(V1,1);
R=sum(V1,2);
flag=isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%% 结果显示
if flag==1
   % 计算初始路径长度
   sort_rand=randperm(N);
   citys_rand=citys(sort_rand,:);
   Length_init=dist(citys_rand(1,:),citys_rand(end,:)');
   for i=2:size(citys_rand,1)
       Length_init=Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
   end
   % 绘制初始路径
   figure(1)
   plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['   ' num2str(i)])
   end
   text(citys_rand(1,1),citys_rand(1,2),['       起点' ])
   text(citys_rand(end,1),citys_rand(end,2),['       终点' ])
   title(['优化前路径(长度：' num2str(Length_init) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 计算最优路径长度
   [V1_max,V1_ind]=max(V1);
   citys_end=citys(V1_ind,:);
   Length_end=dist(citys_end(1,:),citys_end(end,:)');
   for i=2:size(citys_end,1)
       Length_end=Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
   end
   disp('最优路径矩阵');V1
   % 绘制最优路径
   figure(2)
   plot([citys_end(:,1);citys_end(1,1)],...
       [citys_end(:,2);citys_end(1,2)],'o-')
   for i=1:length(citys)
       text(citys(i,1),citys(i,2),['  ' num2str(i)])
   end
   text(citys_end(1,1),citys_end(1,2),['       起点' ])
   text(citys_end(end,1),citys_end(end,2),['       终点' ])
   title(['优化后路径(长度：' num2str(Length_end) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 绘制能量函数变化曲线
   figure(3)
   plot(1:iter_num,E);
   ylim([0 2000])
   title(['能量函数变化曲线(最优能量：' num2str(E(end)) ')']);
   xlabel('迭代次数');
   ylabel('能量函数');
else
   disp('寻优路径无效');
end
%% 连续Hopfield神经网络的优化—旅行商问题优化计算
% function TSP_hopfield()
%% 清空环境变量、定义全局变量
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
% step 1
A=1.5;
D=1;
u0=0.02;
step=0.01;
% step 2
N=8;
DistanceCity=dist(citys,citys');
% step 3
u=2*rand(N,N)-1;
U=0.5*u0*log(N-1)+u;
V=(1+tanh(U/u0))/2;
end

세, 실행 결과

네, 비고

완전한 코드 또는 쓰기 추가 QQ1564658423 과거 검토
>>>>>>
[예측 모델] matlab 입자 군집을 기반으로 한 lssvm 예측 [Matlab 소스 코드 103 포함]
[lSSVM 예측] matlab 고래 최적화 알고리즘을 기반으로 한 lSSVM 데이터 예측 [Matlab 소스 코드 포함] 104]
[lstm 예측] matlab 고래 최적화 알고리즘 기반 lstm 예측 개선 [Matlab 소스 코드 105 포함]
[SVM 예측] matlab bat 알고리즘 기반 SVM 예측 개선 (1) [Matlab 소스 코드 106 포함]
[ SVM 예측】 기반 matlab grey wolf 알고리즘은 svm 지원 벡터 머신 예측을 최적화하기 위해 [Matlab 소스 코드 107 포함]
[예측 모델] matlab BP 신경망 예측 기반 [Matlab 소스 코드 108 포함]
[lssvm 예측 모델] 박쥐 알고리즘을 기반으로 개선 된 최소 제곱 지원 벡터 머신 lssvm 예측 [Matlab 109 이슈]
[lssvm 예측] 나방 소화 알고리즘 기반의 최소 제곱 지원 벡터 머신 lssvm 예측 개선 [Matlab 110]
[SVM 예측] matlab bat 알고리즘 기반 SVM 예측 개선 (2 개) [Matlab 소스 코드 141 포함 기간]

[Lssvm 예측] matlab 나방 소방 알고리즘을 기반으로 한 최소 제곱 지원 벡터 머신 lssvm 예측 개선 [Matlab 소스 코드 142 포함]
[ANN 예측 모델] matlab 차이 알고리즘 기반으로 ANN 네트워크 예측 개선 [Matlab 소스 코드 151 포함]
[예측 모델] matlab RBF 신경망 예측 모델 기반 [Matlab 소스 코드 177주기 포함]
[예측 모델] matlab SVM 회귀 예측 알고리즘 기반으로 주식 동향을 예측 [Matlab 소스 코드 180주기 포함]
[예측 모델] matlab BP 신경 기반 네트워크 모델 최적화 예측 [Matlab 소스 코드 221 포함]
[예측 모델] matlab RLS 알고리즘 기반 데이터 예측 [Matlab 소스 코드 222 포함]
[예측 모델] MATLAB 탄소 배출 제약 조건에 따른 석탄 소비량 최적 예측 [Matlab 소스 코드 223 포함] ]