2022 심천 컵 C 자율 주행 전기 재료 차량 스왑 스테이션 부지 선정 및 일정 계획
우리나라의 2030년 '탄소피킹' 목표, 2060년 '탄소중립'을 달성하기 위해 친환경 자율주행 전기차를 물질운송에 활용하는 것이 발전 추세다. 전기차 출동계획을 수립할 때 배터리 충전 및 교체에 소요되는 시간 비용을 고려해야 하며, 새로운 차량 운송 위치 선정 및 출차 문제를 제시한다.
질문 1 한 묶음의 자율주행 전기자재 트럭이 P 지점에서 D 지점으로 자재를 운송한 다음 빈 채로 반환 하는 등의 방식
으로 진행됩니다. P 지점과 D 지점 사이의 양방향 같은 위치(고속 휴게소와 같은) 스왑 스테이션의 위치와 해당 차량 및 배터리 팩 스케줄링 체계를 결정하기 위해 수학적 프로그래밍 모델을 수립해야 합니다. 지정된 시간 내에 배송을 최대화하기 위해 자재의 양이 자원 제약 및 배터리 작동 모드 제약을 충족합니다. 부록에 주어진 데이터에 따라 계획 모델을 풀고 스왑 스테이션의 위치를 주고 1000 시간 동안 운송 된 자재의 양, 사용 된 차량 수, 배터리 팩 수 및 구체적인 일정 계획을 제공하십시오. 차량 및 배터리 팩.
질문 2 질문 1에서 스테이션 건설 조건을 "포인트 P와 포인트 D 사이의 각 방향에서 전력 교환소의 위치 결정"으로 변경하고, 다른 조건 및 작업은 질문 1과 동일합니다.
Question 3 피크 및 밸리 전기요금, 배터리팩 구입, 충전소 및 교환소 건설 등의 비용을 고려하여, 최소의 일일 수송량과 가장 낮은 투자 및 운영 비용을 보장하는 스테이션 건설 및 배터리팩 일정 계획을 수립하십시오. 3년 정산 주기에서. 부록에 제공된 데이터(기본 데이터는 자체적으로 보완됨)에 따라 구체적인 계산 예가 제공됩니다. 문제 4 여러 승하차 지점과 단일 하역 지점에 대해 위에서 언급한 스왑 스테이션 위치 선택 및 차량 배터리 그룹 일정 문제를 연구합니다.
부록: 데이터 형식(제한적)
계산 예제 데이터는 다음 형식 제한에 따라 자체적으로 컴파일되며 통합 테스트 계산 예제 데이터는 결승전에 공개됩니다.
(1) P지점에서 D지점까지 : 주행거리 10km, 양방향 단일차량(철도) 전용차로, 차량간격 200m 이상
(2) 차량 : 60km/h의 속도로 125대, 각 차량 6개의 배터리 팩으로 평가되며, 처음에는 스왑 스테이션의 무부하 상태이고 각 온보드 배터리 팩의 SoC(충전 상태)는 100%입니다.
(3) 배터리: 900개 그룹, 단일 배터리 그룹이 독립적으로 계량되고, 차량 내 6개 배터리 그룹의 전력 소비가 일정하며, 각 배터리 그룹의 SoC가 빈 차량을 운전할 때 3분마다 1% 감소합니다. 그리고 각 배터리 그룹의 SoC는 트럭이 배터리 팩의 SoC가 1% 감소할 때마다 2분마다 1% 감소합니다. 온보드 배터리 팩의 SoC는 [10 %, 25%]. 교체용 배터리 팩의 SoC는 100%
이며, 각 배터리 팩을 충전 및 감지하여 교체 후 대기 상태로 전환하는 데 20초가 소요됩니다. 로드 및 언로딩에 각각 1분 소요
자동 배터리 교체 장비 가격, 배터리 가격, 차량 가격.
모델 구축 및 솔루션 분석:
가장 먼저 고려해야 할 것은 배터리 용량이 10%에서 25%에 도달할 때까지 전력 교환소에서 포인트 P, 포인트 D, 포인트 P까지 배터리 교체를 위해 전력 교환 스테이션으로 이동하는 것
입니다.여기에서 회로를 그릴 수 있습니다. 도표
S 2차선 도로의 길이는 10km, 즉 10,000m
이고, 두 차량 사이의 거리는 200m 이상입니다.은 무슨 뜻인가요?
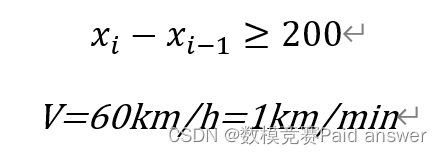
벤츠 트램은 차의 길이를 고려하지 않고 도로에 최대 100개 정도 운행되고 있는데,

질문에 따르면 배터리는 900개 그룹, 단일 배터리 그룹은 독립적으로 측정되며, 6개의 온보드 배터리 그룹은 같은 양의 전력을 소모한다. .
IQ 밸런스가 부족해요 6개의 배터리를 일괄로 충전하고 배터리를 일괄로 교체하는 상황은 고려하지 않습니다 모델의 가정에 직접 씁니다 : 전기 자동차가 배터리로 교체되고 6개 단일 배터리를 개별적으로 교체하는 것을 무시하고 배터리 팩을 함께 교체합니다.화물 용량의 영향.
그것도 일괄적으로 배터리 교체를 하고, 교체 스테이션의 위치, 최대 화물량, 시간 1000h=60000min, 6개 배터리를 10%에 가깝게 사용하고 일괄 교체한 차이가 영향을 미칠 것으로 알고 있습니다. 전체 900개 그룹.배터리 사용량은 많지만 이 배터리 교체 프로그램은 계산하기가 쉽지 않습니다. 이 질문의 의미는 정수 계획법과 선형 계획법의 조합을 사용하도록 요청하는 것입니다. 100개의 트램이 도로를 달리고 있고 나머지 배터리는 최대한 낭비하지 않고 충전됩니다. 그러면 배터리가 완전히 충전됩니다. 자동차가 10%까지 달릴 때 충전됩니다. 배터리를 교체하는 방법? 최대 화물량을 달성할 수 있습니다.
발전소 위치는 계산하기 쉽지만 배터리 교체 분배 방식은 그렇지 않은 이유를 말씀드리자면 배터리가 6개라면 배터리 교체 방식이 있다면 C6이 1개를 선택하게 하기 때문입니다. , 6가지 배터리 교체 방식, 그리고 비교하거나 최적의 배터리 교체 솔루션을 제시하는 것은 IQ인데 왜 6가지 솔루션이 있을까요? 전기의 25%-10%=15%는 다른 전기를 추가하거나 전기를 반환하기 위해 앞뒤로 움직일 수 있기 때문에 발전소에 갈 수 있는 남은 전기가 있는지 확인해야 하므로 갈 수 없습니다. 두 번째로, 당신은 단지 정직하게 전기를 변경할 수 있습니다, 이해?
최종 결과
첫 번째 질문과 마지막으로 스왑 스테이션이 P에서 D까지 5km에 스왑 스테이션을 건설하는 것임을 확인합니다. 배터리 교체 계획과 관련하여 배터리 전체를 사용하여 효율성을 극대화하려면 어떻게 해야 합니까? 교통량은 차수와 트램이 P에 도달하는 횟수와 관련이 있고 배터리는 차수와 P에 도착하는 횟수에 영향을 미칩니다. 독자 여러분, 이 모퉁이를 돌셨습니까?
두 번째 질문의 최종 결과는 왕복 20/3km 지점에 발전소를 건설하는 것입니다. 세 번째
질문 결과는 변화점의 시점, 주야간 변경 방법, 산업용 전력 시간 사용 방법, 전력 교환 전략 계획의 최저 가격 및 최고 가격을 고려해야 합니다.
대기열 이론 알고리즘
아이디어가 마침내 완성 되었다고 생각합니다.
위의 내용은 주제에 대한 개인적인 이해를 나타냅니다.

프로그램 코드 예:
import math # 导⼊模块
import random # 导⼊模块
import pandas as pd # 导⼊模块 YouCans, XUPT
import numpy as np # 导⼊模块 numpy,并简写成 np
import matplotlib.pyplot as plt
from datetime import datetime
# ⼦程序:定义优化问题的⽬标函数
def cal_Energy(X, nVar, mk): # m(k):惩罚因⼦,随迭代次数 k 逐渐增⼤
p1 = (max(0, 6*X[0]+5*X[1]-60))**2
p2 = (max(0, 10*X[0]+20*X[1]-150))**2
fx = -(10*X[0]+9*X[1])
return fx+mk*(p1+p2)
# ⼦程序:模拟退⽕算法的参数设置
def ParameterSetting():
cName = "funcOpt" # 定义问题名称 YouCans, XUPT
nVar = 2 # 给定⾃变量数量,y=f(x1,..xn)
xMin = [0, 0] # 给定搜索空间的下限,x1_min,..xn_min
xMax = [8, 8] # 给定搜索空间的上限,x1_max,..xn_max
tInitial = 100.0
tFinal = 1
alfa = 0.98
meanMarkov = 100 # Markov链长度,也即内循环运⾏次数
scale = 0.5 # 定义搜索步长,可以设为固定值或逐渐缩⼩
return cName, nVar, xMin, xMax, tInitial, tFinal, alfa, meanMarkov, scale
# 模拟退⽕算法
def OptimizationSSA(nVar,xMin,xMax,tInitial,tFinal,alfa,meanMarkov,scale):
# ====== 初始化随机数发⽣器 ======
randseed = random.randint(1, 100)
random.seed(randseed) # 随机数发⽣器设置种⼦,也可以设为指定整数
# ====== 随机产⽣优化问题的初始解 ======
xInitial = np.zeros((nVar)) # 初始化,创建数组
for v in range(nVar):
# xInitial[v] = random.uniform(xMin[v], xMax[v]) # 产⽣ [xMin, xMax] 范围的随机实数
xInitial[v] = random.randint(xMin[v], xMax[v]) # 产⽣ [xMin, xMax] 范围的随机整数
# 调⽤⼦函数 cal_Energy 计算当前解的⽬标函数值
fxInitial = cal_Energy(xInitial, nVar, 1) # m(k):惩罚因⼦,初值为 1
# ====== 模拟退⽕算法初始化 ======
xNew = np.zeros((nVar)) # 初始化,创建数组
xNow = np.zeros((nVar)) # 初始化,创建数组
xBest = np.zeros((nVar)) # 初始化,创建数组
xNow[:] = xInitial[:] # 初始化当前解,将初始解置为当前解
xBest[:] = xInitial[:] # 初始化最优解,将当前解置为最优解
fxNow = fxInitial # 将初始解的⽬标函数置为当前值
fxBest = fxInitial # 将当前解的⽬标函数置为最优值
print('x_Initial:{:.6f},{:.6f},\tf(x_Initial):{:.6f}'.format(xInitial[0], xInitial[1], fxInitial))
recordIter = [] # 初始化,外循环次数
recordFxNow = [] # 初始化,当前解的⽬标函数值
recordFxBest = [] # 初始化,最佳解的⽬标函数值
recordPBad = [] # 初始化,劣质解的接受概率
kIter = 0 # 外循环迭代次数
totalMar = 0 # 总计 Markov 链长度
totalImprove = 0 # fxBest 改善次数
nMarkov = meanMarkov # 固定长度 Markov链
# ====== 开始模拟退⽕优化 ======
# 外循环
tNow = tInitial # 初始化当前温度(current temperature)
while tNow >= tFinal: # 外循环
kBetter = 0 # 获得优质解的次数
kBadAccept = 0 # 接受劣质解的次数
kBadRefuse = 0 # 拒绝劣质解的次数
# ---内循环,循环次数为Markov链长度
for k in range(nMarkov): # 内循环,循环次数为Markov链长度
totalMar += 1 # 总 Markov链长度计数器
# ---产⽣新解
# 产⽣新解:通过在当前解附近随机扰动⽽产⽣新解,新解必须在 [min,max] 范围内
# ⽅案 1:只对 n元变量中的⼀个进⾏扰动,其它 n-1个变量保持不变
xNew[:] = xNow[:]
v = random.randint(0, nVar-1) # 产⽣ [0,nVar-1]之间的随机数
xNew[v] = round(xNow[v] + scale * (xMax[v]-xMin[v]) * random.normalvariate(0, 1))
# 满⾜决策变量为整数,采⽤最简单的⽅案:产⽣的新解按照四舍五⼊取整
xNew[v] = max(min(xNew[v], xMax[v]), xMin[v]) # 保证新解在 [min,max] 范围内
# ---计算⽬标函数和能量差
# 调⽤⼦函数 cal_Energy 计算新解的⽬标函数值
fxNew = cal_Energy(xNew, nVar, kIter)
deltaE = fxNew - fxNow
# ---按 Metropolis 准则接受新解
# 接受判别:按照 Metropolis 准则决定是否接受新解
if fxNew < fxNow: # 更优解:如果新解的⽬标函数好于当前解,则接受新解
accept = True
kBetter += 1
else: # 容忍解:如果新解的⽬标函数⽐当前解差,则以⼀定概率接受新解
pAccept = math.exp(-deltaE / tNow) # 计算容忍解的状态迁移概率
if pAccept > random.random():
accept = True # 接受劣质解
kBadAccept += 1
else:
accept = False # 拒绝劣质解
kBadRefuse += 1
# 保存新解
if accept == True: # 如果接受新解,则将新解保存为当前解
xNow[:] = xNew[:]
fxNow = fxNew
if fxNew < fxBest: # 如果新解的⽬标函数好于最优解,则将新解保存为最优解
fxBest = fxNew
xBest[:] = xNew[:]
totalImprove += 1
scale = scale*0.99 # 可变搜索步长,逐步减⼩搜索范围,提⾼搜索精度
# ---内循环结束后的数据整理
#
pBadAccept = kBadAccept / (kBadAccept + kBadRefuse) # 劣质解的接受概率
recordIter.append(kIter) # 当前外循环次数
recordFxNow.append(round(fxNow, 4)) # 当前解的⽬标函数值
recordFxBest.append(round(fxBest, 4)) # 最佳解的⽬标函数值
recordPBad.append(round(pBadAccept, 4)) # 最佳解的⽬标函数值
아이디어가 마침내 완성되었습니다. 방해를 환영합니다.