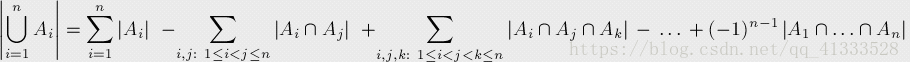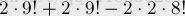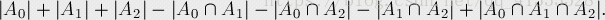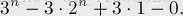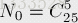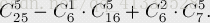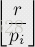组合数学基础

一、加法原理&乘法原理

小学数学略

二、错排问题

当n个编号元素放在n个编号位置，编号与位置不对应的方法数用D(n)表示

求解D（n）：

第一步，把第n个元素放在一个位置，比如位置k，一共有n-1种方法；

第二步，放编号为k的元素，这时有两种情况：

⑴把它放到位置n，那么，对于剩下的n-1个元素，由于第k个元素放到了位置n，剩下n-2个元素就有D(n-2)种方法；

⑵第k个元素不把它放到位置n，这时，对于这n-1个元素，有D(n-1)种方法；

综上得到

D(n) = (n-1) [D(n-2) + D(n-1)]

特殊地，D(1) = 0, D(2) = 1

为方便起见，设D(k) = k! N(k), k = 1, 2, …, n,

则N(1) = 0, N(2) = 1/2

n ≥ 3时，n! N(n) = (n-1) (n-1)! N(n-1) + (n-1)! N(n-2)

即 nN(n) = (n-1) N(n-1) + N(n-2)

于是有N(n) - N(n-1)=（N(n-1) - N(n-2)）/（-n）=(-1)^(n-2) / n!=(-1)^(n)/ n!

N(n-1) - N(n-2) = (-1)^(n-1) / (n-1)!,

N(2) - N(1) = (-1)^2 / 2!.

相加，可得

N(n) = (-1)^2/2! + … + (-1)^(n-1) / (n-1)! + (-1)^n/n!

因此

D(n) = n! [(-1)^2/2! + … + (-1)^(n-1)/(n-1)! + (-1)^n/n!].

三、容斥原理

摘录点击打开链接这个的前面比较精华的部分：

容斥原理：要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

例①：由0到9的数字组成排列，要求第一个数大于1，最后一个数小于8，一共有多少种排列？

我们可以来计算它的逆问题，即第一个元素<=1或者最后一个元素>=8的情况。我们设第一个元素<=1时有X组排列，最后一个元素>=8时有Y组排列。那么通过容斥原理来解决就可以写成：

即

再用10！一减就是答案了

例②：长度为n的由数字0，1，2组成的序列，要求每个数字至少出现1次，这样的序列有多少种？

同样的，我们转向它的逆问题，我们定义Ai(i=0…2)表示不出现数字i的序列数，那么由容斥原理，我们得到该逆问题的结果为：

可以发现每个Ai的值都为2^n（因为这些序列中只能包含两种数字）。而所有的两两组合都为1（它们只包含1种数字）。最后，三个集合的交集为0。（因为它不包含数字，所以不存在）要记得我们解决的是它的逆问题，所以要用总数减掉，得到最终结果：

例③：求整数解有多少组？已知：

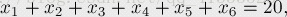
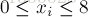
我们先不去理会xi<=8的条件，来考虑所有正整数解的情况。这个很容易用组合数来求解，我们要把20个元素分成6组，也就是添加5块“夹板”，然后在25个位置中找5块“夹板”的位置。

然后通过容斥原理来讨论它的逆问题，也就是x>=9时的解。我们定义Ak为xk>=9并且其他xi>=0时的集合，同样我们用上面的添加“夹板”法来计算Ak的大小，因为有9个位置已经被xk所利用了，所以：

因为所有x的和不能超过20，所以三个或三个以上这样的集合时是不能同时出现的，它们的交集都为0。最后我们用总数剪掉用容斥原理所求逆问题的答案，就得到了最终结果：

例④：区间[1,r]上与n互素的个数

去解决它的逆问题，求不与n互素的数的个数。考虑n的所有素因子pi(i=1…k)在[1;r]中有多少数能被pi整除呢？它就是：

然而，如果我们单纯将所有结果相加，会得到错误答案。有些数可能被统计多次（被好几个素因子整除）。所以，我们要运用容斥原理来解决。我们可以用2^k的算法求出所有的pi组合，然后计算每种组合的pi乘积，通过容斥原理来对结果进行加减处理。

例⑤：求120以内的素数个数

由于120以内的合数一定是2，3，5，7的倍数，而且不可能一个合数的因数都超过11（11*11=121），所以120以内素数的反面就是120以内2，3，5，7的倍数；然后求各种集合的交并结果，加减得到27，但是这并不最终答案，因为2，3，5，7被排出了，但他们是素数，1不是素数却没有排除，所以答案是27+4-1=30

四、鸽巢原理（抽屉原理）

原理1：多余mn个物品放入n个抽屉，总有一个抽屉有至少m+1个物品

原理2：少于mn个物品放入n个抽屉，总有一个抽屉有至多m-1个物品

鸽巢原理是专门用来解决存在性问题的

例①，2，4，6，……，30这15个偶数中任意取9个，必有两个和是34

构造抽屉(4+30),(6+28),...,(16,18),(2)一共8个抽屉，选9个必定有两个在一个抽屉里面，故得证

例②，1，2，3，……，20至少任选多少个，可保证一定有两个数的差是12

例③，1，2，3，……，20任取11个数，必定有两个满足倍数关系

构造抽屉，每个抽屉里面的数两两互为倍数关系：(1,2,4,8,16),(3,6,12),(5,10,20),(7,14),(9,18),11,13,15,17,19,一共10个人抽屉

例④，n个人握手，至少有2个人握手次数一样

若有一个人一次手都没握，那么最多握手次数是n-2；如果一个人握了n-1次手，那么最少握手次数是1，也就是说握手次数的可能情况最多n-1种可能，易证结论成立

例⑤，任取8个数，必有两个的差是7的倍数

按照余数构造抽屉，易证

例⑥，对于任意5个自然数，任取三个，和一定是3的倍数

例⑦，对于任意11个自然数，一定存在6个数，和是6的倍数

11取3，必为3倍数；8取3，必为3倍数；5取3，必为3倍数；

三次取的三个数的和，是三个数，这三个和，一定可以找到两个，和是2的倍数，故得证

例⑧，任意给定7个数，必存在两个，要么和是10的倍数，要么差是10的倍数

构造抽屉：按余数：0，1，2，……，9，再把6&4，7&3，8&2，9&1合并，共六组，易得证

例⑨，平面上六个点，每个点之间连一条边，要么红色，要么黑色，一定存在同色三角形

考察一个点的5条边，必有三条同色，不妨设为红色，这三条红边的另一端可以构成三条边，在这还没确定三条边中，只要存在一条红边，那么就出现红色的同色三角形，如果都是黑色，那么就形成黑色的同色三角形

例⑨变换，六个人的会议，至少有三个人认识或至少有三个人不认识

例⑩，17个人互相通信，讨论话题，话题一共就3种，一定存在3个人的话题相同

一个人连16条边，至少有6条同色（设为颜色1），六条边的端点构成的边中，只要有一条为颜色1，就满足，若都不是颜色1，那么就是六个人中只用两种颜色连，一定存在同色三角形，故成立