【问题描述】
-
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
-
例如:
A1是A(5*10)的矩阵;A2是A(10*15)的矩阵;
A3是A(15*2)的矩阵;
那么就有两种计算方式:
1.(A1A2)A3
2. A1(A2A3)
第一种乘法次数为:5 * 10 * 15+5 * 15 * 2=900
第二种乘法次数为:10 * 15 * 2+5 * 10 * 2=400
显然,最好的次序是(A1A2)A3,乘法次数为400次。 -
矩阵链乘法问题描述:
给定由n个矩阵构成的序列{A1,A2,…,An},对乘积A1A2…An,找到最小乘法次数的序列乘法次序,即加括号方法。 -
动态规划解题思路

-
寻找最优子结构
对乘积A1A2…An的任意加括号方法都会将序列在某个地方分成两部分,也就是最后一次乘法计算的地方,我们将这个位置记为k,也就是说首先计算A1…Ak和Ak+1…An,然后再将这两部分的结果相乘。
最优子结构:假设A1A2…An的一个最优加括号把乘积在Ak和Ak+1间分开,则前缀子链A1…Ak的加括号方式必定为A1…Ak的一个最优加括号,后缀子链同理。
一开始并不知道k的确切位置,需要遍历所有位置以保证找到合适的k来分割矩阵的连乘。 -
建立递归关系

-
构建辅助表,解决重叠子问题
从第二步的递归式可以发现解的过程中会有很多重叠子问题,可以用一个n*n维的辅助表m[n][n] s[n][n]分别表示最优乘积代价及其分割位置k 。
辅助表s[n][n]由自底向上填表构建,该方法要求按照递增的方式逐步填写子问题的解,也就是先计算长度为2的所有矩阵链的解,然后计算长度3的矩阵链,直到长度n。 -
例题:
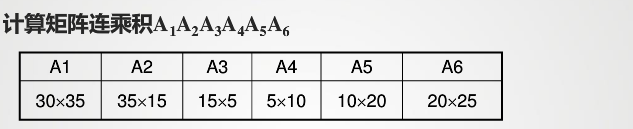
-
构建辅助表:
计算顺序:

计算过程:

m[i][j]计算结果:

s[i][j]计算结果:

-
自底向上递推并用二维数组保存中间结果避免重复计算
-
核心代码:
void MatrixChainOrder(int *p,int m[N][N],int s[N][N],int length)
{
int n=length-1;
int l,i,j,k,q=0;
//m[i][i]只有一个矩阵,所以相乘次数为0,即m[i][i]=0;
for(i=1;i<length;i++)
{
m[i][i]=0;
}
//l表示矩阵链的长度
// l=2时,计算 m[i,i+1],i=1,2,...,n-1 (长度l=2的链的最小代价)
for(l=2;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1; //以i为起始位置,j为长度为l的链的末位,
m[i][j]=0x7fffffff;//先假定最小代价为int类型所能取到的最大值
//k从i到j-1,以k为位置划分
for(k=i;k<=j-1;k++)
{
q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
}
}
}
cout << "最小的次数为:\n"<<m[1][N-1] << endl;
}
void PrintAnswer(int s[N][N],int i,int j)
{
if(i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
PrintAnswer(s,i,s[i][j]);
PrintAnswer(s,s[i][j]+1,j);
cout<<")";
}
}
- 完整源代码:
#include<iostream>
using namespace std;
const int N=7;
//p为矩阵链,p[0],p[1]代表第一个矩阵,p[1],p[2]代表第二个矩阵,length为p的长度
//所以如果有六个矩阵,每个矩阵的行和最后一个矩阵的列,所以length=7,m为存储最优结果的二维矩阵,s为存储选择最优结果路线的
//二维矩阵
void MatrixChainOrder(int *p,int m[N][N],int s[N][N],int length)
{
int n=length-1;
int l,i,j,k,q=0;
//m[i][i]只有一个矩阵,所以相乘次数为0,即m[i][i]=0;
for(i=1;i<length;i++)
{
m[i][i]=0;
}
//l表示矩阵链的长度
// l=2时,计算 m[i,i+1],i=1,2,...,n-1 (长度l=2的链的最小代价)
for(l=2;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1; //以i为起始位置,j为长度为l的链的末位,
m[i][j]=0x7fffffff;//先假定最小代价为int类型所能取到的最大值
//k从i到j-1,以k为位置划分
for(k=i;k<=j-1;k++)
{
q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
}
}
}
cout << "最小的次数为:\n"<<m[1][N-1] << endl;
}
void PrintAnswer(int s[N][N],int i,int j)
{
if(i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
PrintAnswer(s,i,s[i][j]);
PrintAnswer(s,s[i][j]+1,j);
cout<<")";
}
}
int main()
{ int p[N],x,i;
int m[N][N],s[N][N];
cout<<"请依次输入每个矩阵的行和最后一个矩阵的列数:"<<endl;
for(i=0;i<N;i++)
cin>>p[i];
MatrixChainOrder(p,m,s,N);
PrintAnswer(s,1,N-1);
return 0;
}
- 运行截图:

部分图来源于网上。

