树状数组总结(不看后悔系列）

最近准备学深点树状数组，在原来的文章上添写内容。

文章目录

定义
结构起源
预备函数—— $lowbit$ 函数

关于树状数组的理解

二维树状数组
功能

1、查询区间前缀和
2、单点修改，维护前缀和

树状数组的构造
树状数组黑科技
离散化
例题讲解

定义

树状数组或二元索引树（英语：Binary Indexed Tree/(BIT)），又以其发明者命名为Fenwick树，其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和，区间和。它可以 $O(\log n)$ 的时间得到任意前缀和 $\sum _{i=1}^{j}A[i],1<=j<=N}{\displaystyle$ ，并同时支持在 $O(\log n)$ 时间内支持动态单点值的修改。空间复杂度 $O(n)$ 。

结构起源

按照Peter M. Fenwick的说法，正如所有的整数都可以表示成2的幂和，我们也可以把一串序列表示成一系列子序列的和。采用这个想法，我们可将一个前缀和划分成多个子序列的和，而划分的方法与数的2的幂和具有极其相似的方式。一方面，子序列的个数是其二进制表示中1的个数，另一方面，子序列代表的f[i]的个数也是2的幂。

预备函数—— $lowbit$ 函数

定义一个 $lowbit$ 函数，返回参数转为二进制后,最后一个1的位置所代表的数值.
求法：

int lowbit(int x){ return x & (-x);}

列如 $6: 0110$ ，返回的是2

关于树状数组的理解

借助 oi wiki 一张图来描述。
在这里插入图片描述

定义树状数组 $C$

$C$ 中节点 $x$ 维护原数组 $A$ 的区间和 $[x-lowbit(x)+1,x]$ 。
即
$C[x]=\sum\limits_{i=x-lowbit(x)+1}^{x}A[i]$

所以在构造树状数组的时候可以前缀和 $O(n)$ 构造。

然后举个例子，对于 $x=7=2^2+2^1+2^0$ ，区间 $[1,7]$ 可以分解为 $[1,4],[5,6],[7,7]$ 三个小区间，每个区间的长度对应着二进制分解后的大小，且每个小区间的长度也等于区间右段点的 $lowbit$ 的值。

该结构满足如下性质：
1、每个内部节点 $c[x]$ 保存以它为根的子树中所有叶节点的和。

2、每个内部节点 $c[x]$ 的子节点个数等于 $lowit(x)$ 的位数

3、除树根外，每个内部节点 $c[x]$ 的父节点是 $c[x+lowbit(x)]$

4、树的深度为 $O(log(N))$

然后下面是引用知乎上得一句话。

我们知道树状数组是可以用来求前缀和的。而线段树树求前缀和时是不需要右儿子的，所以把右儿子全部去掉，只保留左区间就是BIT了。

而维护的区间则是[i-lowbit(x)+1,i];其中lowbit为结点i二进制最低位1的值。而lowbit操作就是这课二叉树的层，而BIT的实质上也是在Binary上建个tree。所以modify的时候就沿着边往上爬；求前缀和时就往下爬。

但还有个问题就是，区间修改，然后再单点查询怎么办？这时就在tree上构建差分数组，然后每次change的时候<就只修改[l,+k],[r+1,-k]即可。之后再把要查询的加起来就是了。————————————————Violetinori

二维树状数组

二维树状数组常用来维护子矩阵的和。
和一维类似，二维树状数组每一维都是树状数组。
例：举个例子来看看C[][]的组成。
设原始二维数组为：
　 $A[][]$ ={{ $a11,a12,a13,a14,a15,a16,a17,a18,a19$ },
$\ \ \ \qquad$ { $a21,a22,a23,a24,a25,a26,a27,a28,a29$ },
$\ \ \ \qquad$ { $a31,a32,a33,a34,a35,a36,a37,a38,a39$ }，
$\ \ \ \qquad$ { $a41,a42,a43,a44,a45,a46,a47,a48,a49$ }};
C[1][1]=a11,C[1][2]=a11+a12,C[1][3]=a13,C[1][4]=a11+a12+a13+a14,c[1][5]=a15,C[1][6]=a15+a16,…
这是A[][]第一行的一维树状数组

C[2][1]=a11+a21,C[2][2]=a11+a12+a21+a22,C[2][3]=a13+a23,C[2][4]=a11+a12+a13+a14+a21+a22+a23+a24,
C[2][5]=a15+a25,C[2][6]=a15+a16+a25+a26,…
这是A[][]数组第一行与第二行相加后的树状数组

C[3][1]=a31,C[3][2]=a31+a32,C[3][3]=a33,C[3][4]=a31+a32+a33+a34,C[3][5]=a35,C[3][6]=a35+a36,…
这是A[][]第三行的一维树状数组

C[4][1]=a11+a21+a31+a41,C[4][2]=a11+a12+a21+a22+a31+a32+a41+a42,C[4][3]=a13+a23+a33+a43,…
这是A[][]数组第一行+第二行+第三行+第四行后的树状数组

ll c[N+5][N+5];
int n,m;
inline int lowbit(int x) {return x&(-x);}
void add(int i,int j,int val){
    for(int x = i;x <= n;x += lowbit(x))
        for(int y = j;y <= m;y += lowbit(y))
            c[x][y] += val;
}
ll ask(int i,int j){
    ll ans = 0;
    for(int x = i;x>0;x -= lowbit(x))
        for(int y = j;y > 0;y -= lowbit(y))
            ans += c[x][y];
    return ans;
}
ll sum(int x,int y,int xx,int yy){
    x --;y --;
    return ask(xx,yy) - ask(xx,y) - ask(x,yy) + ask(x,y);
}

功能

说到底，树状数组最主要的作用就是动态维护前缀和。
注意：树状数组的下标必须从1开始，，因为lowbit(0)=0,如果从0开始的话就会陷入死循环！！树状数组适用于所有满足结合律的运算（加法，乘法，异或等）

1、查询区间前缀和

从上面我们可以知道， $[1,7]$ 在树状数组中被分解为3个小区间，每个小区间为 $[x-lowbit(x)+1,x]$ 。而 $x$ 是树状数组中的节点。所以要查询 $[1,7]$ 的前缀和，只需要从顶点 $7$ 不断往下跳 $lowbit$ 累加即可。

int ask(int x){
    int ans = 0;
    while(x){
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}

所以我们要求 $[l,r]$ 的区间和，区间和满足区间可减性，即 $ask(r)-ask(l-1)$ ,

2、单点修改，维护前缀和

注意在树状数组中包含原数组中 $a[x]$ 的只有 $c[x]$ 及其它的祖先节点。并且任意节点的祖先至多有 $log(N)$ 个。所以我们在 $x$ 点边修改边网上跳 $lowbit$ 即可。

void add(int x,int y){//n为区间上界
    for(;x <= n;x += lowbit(x)) c[x] += y;
}

树状数组的构造

比较一般的是直接建立一个全为 $0$ 的数组 $c$ ，然后对每个位置 $x$ 执行 $add(x,a[x])$ ,时间复杂度 $O(nlog(N))$

for(int i = 1;i <= n;++i) add(i,a[i]);

关于 $O(N)$ 的构造上面已经提到了，因为每个节点 $x$ 以它为右端点，长度为 $lowit(x)$ 的一段区间，所以我们边维护原数组 $a$ 的前缀和，边构造 $c$ 。

void init(){
    for(int i = 1;i <= n;++ i){
        sum[i] = sum[i-1] + a[i];
        c[i] = sum[i] - sum[i-lowbit(i)];
    }
}

还有个 $O(N)$ 构造
每一个节点的值是由所有与自己直接相连的儿子的值求和得到的。因此可以倒着考虑贡献，即每次确定完儿子的值后，用自己的值更新自己的直接父亲。


void init(){
    for(int i = 1;i <= n;++i){
        c[i] += a[i];
        int j = i + lowbit(i);
        if(j <= n) c[j] += c[i];
    }
}

树状数组黑科技

树状数组维护区间最值

我们有上述可以发现，树状数组又似一种分块方式，将 $[1,r]$ 分为若干子区间，然后每个节点维护这一段区间区间和，而如果我们让每个节点维护区间最值（以下假如是最大值），那么类比于查询区间和功能，我们改下得：

int ask(int x){
    int ans = 0;
    while(x){
        ans = max(ans,c[x]);
        x -= lowbit(x);
    }
    return ans;
}

但是却有一个问题，那就是这样只能查询 $[1,x]$ 的最值，而不能查询 $[l,r]$ 的最值，因为区间最值不满足区间可加/减性。但也不妨碍我们使用它，比如在求 $LIS$ 的过程中，原来做法 $n^2$ ，因为每次找前面比他小的最大的 $LIS$ 都要 $O(n)$ 遍历一遍，找到这个最大值，注意此处是找 $[1,i]$ 的最大值，所以我们完全可以使用树状数组来优化这个过程变为 $O(log(n))$ 。这样整体复杂度就降为了 $O(nlog(N))$ ，关于LIS这部分讲解，以后应该会放出来吧。

至于网上其他的改法什么的个人感觉复杂度不大靠谱，还是老老实实学线段树去吧。

$logn$ 求第k小
如果我们把每个值当做下标插入进去 $(add(a_i,1))$ ，我们很容易求的某个数前面有多少个数小于等于它 $(ask(a_i))$ 。 在树状数组中，节点是根据 2 的幂划分的，每次可以扩大 2 的幂的长度 $(倍增思想)$ 。当然这也离不开离散化，我会在最后一道题讲解下这个用法。下面这张图比较直观的说明了树状数组的结构性质。
(图片来自网络)
区间操作

1、区间修改，单点查询————树状数组维护差分数组

树状数组只能查询前缀和和单点修改，我们可以通过设立一个差分数组 $b[\ ]$ ，

并用树状数组维护，那么区间修改就变为了单点修改。如在 $[l,r]$ 的区间内增加一

个 $k$ ，那么 $add(l,k),add(r+1,-k)$ 。这就完成了差分数组的维护，若单点查

询x处的值，只需 $a[x] + ask(x)$ 。

2、区间修改，区间查询————两个树状数组维护（可以用来完成动态区间加等差数列的维护）

由上面我们得知，用树状数组进行区间修改就是维护一个差分数组 $b$ ，对于 $x$ 位置

处增加的值就是 $ask(x)$ ，即 $\sum_{i=1}^{x}b[i]$ ，那么对于原数组 $a[\ ]$ ，数组 $a$ 的前缀和

$S(x)$ 总体增加的值就是 $\sum_{i=1}^{x}\sum_{j=1}^{i}b[j]$

$\sum_{i=1}^{x}\sum_{j=1}^{i}b[j]=$

$\qquad\qquad\sum_{i=1}^{x}(x-i+1)*b[i]=(x+1)\cdot \sum_{i=1}^{x}b[i]-\sum_{i=1}^{x}i\cdot b[i]$

即我们可以用两个树状数组维护上述两个前缀和。。（其中前一个是差分数组，后面是i*差分数组）

具体的说，我们建立两个树状数组c0，c1，起初全部赋值为0.对于每条指令 C l r d 执行四个操作

1、在树状数组c0中把位置 l 上的加上d

2、在树状数组c0中，把位置r+1 上的位置减去d

3、在树状数组c1中，在位置l 上加上l * d

4、在树状数组c1中，在位置r+1上的数减去（r+1）*d

另外，我们建立数组S存储a的原始前缀和。所以对于每条指令 Q l r为：

$[S(r)+(r+1)*ask(c0,r)-ask(c1,r)]-[S(l-1)+l*ask(c0,l-1)-ask(c1,l-1)]$

虽然这样区间修改区间维护这个做法比较麻烦，不如直接用线段树，不过，有时候动态区间加等差数列会产生比较巧妙的用处。

附上算法竞赛进阶指南上的代码

const int SIZE = 100010;
int a[SIZE],n,m;
ll c[2][SIZE],S[SIZE];
int lowbit(int x){return  x&(-x);}
ll ask(int k,int x){
    ll ans = 0;
    for(;x > 0;x -= lowbit(x)) ans += c[k][x];
    return ans;
}
void add(int k,int x,int y){
    for(;x <= n;x += lowbit(x)) c[k][x] += y;
}
int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;++i) scanf("%d",&a[i]),S[i] = S[i-1] + a[i];
    while(m --){
        char op[3];int l,r,d;
        scanf("%s%d%d",op,&l,&r);
        if(op[0] == 'C'){
            scanf("%d",&d);
            add(0,l,d);add(0,r+1,-d);
            add(1,l,l*d);add(1,r+1,-(r+1)*d);
        }
        else {
            ll ans = S[r] + (r+1)*ask(0,r) - ask(1,r);
            ans -= S[l-1] + l *ask(0,l-1) - ask(1,l-1);
            printf("%lld\n",ans);
        }
    }
}

离散化

一些问题用树状数组解决需要离散化，比如给两个数组 $a_i,b_i$ ，这是一个二维偏序 $<a_i,b_i>$ ，然后让你根据题意维护前缀和。但是需要注意的是，时间是一种全序全系， $4s$ 就是比 $3s$ 晚。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=100000;
int a[maxn];
int b[maxn];
int n;
int main()
{
    int m=0;
    cin>>n;//元素个数
    for(int i=1;i<=n;++i)
    {
    scanf("%d",&a[i]);
    b[i]=a[i];//b[]作为离散化的数组
    }
    sort(b+1,b+1+n);//将b数组排序，因为是从b[1]开始存储的，所以要b+1
    m=unique(b+1,b+1+n)-b-1;//去重操作，返回不同元素的个数
    for(int i=1;i<=n;++i)
      a[i] = lower_bound(b+1,b+1+m,a[i]) - b;//映射
    return 0;
}

例题讲解

例题：给你 $n$ 个数， $a_1,a_2.....a_n$ ，然后对于每一个 $i$ 让你求前面有多少值小于它。
$1<=n<=1e5,0<=a_i<=1e9$
思路：
题目说每一个 $i$ 前面有多少元素小于它，位置是一个偏序，且是个全序关系。
这里我们维护的是元素数目的前缀和。插入时，把每个元素的 $a_i$ 当做下标，值为1。
我们正序遍历，然后对于每个 $i$ ，我们先查询小于 $a_i$ 的前缀和，然后在执行插入 $add(a[i],1)$ 。
但是 $a_i$ 的范围很大，我们不关心 $a_i$ 的大小，我们在乎的是 $a_i$ 之间的大小关系。所以我们将 $a_i$ 离散化，就是将这些值映射为一组排名。

poj2299
题意：让你求有多少逆序对。
思路：相比于上个例题，这个是让求后面有多少个元素小于他，所以我们倒序插入处理，做法类似于上面。
注意开long long。。。

ll c[N];int n;
inline int lowbit(int x){return x & (-x);}
ll ask(int x){
    ll ans = 0;
    while(x){
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}
void add(int x,int y){
    for(;x <= n;x += lowbit(x)) c[x] += y;
}
int a[N],b[N];
int main(){
    while(scanf("%d",&n) == 1&&n){
        memset(c,0,sizeof c);
        for(int i = 1;i <= n;++i) scanf("%d",&a[i]),b[i] = a[i];
        sort(b + 1,b + n + 1);
        int m = unique(b+1,b+n+1) - b - 1;
        for(int i = 1;i <= n;++i) a[i] = lower_bound(b+1,b+m+1,a[i]) - b;
        ll ans = 0;
        for(int i = n;i >= 1;i --){
            ans += ask(a[i]-1);
            add(a[i],1);
        }
        printf("%lld\n",ans);
        //bug;
    }
}

在 $poj$ 跑了接近800ms，接下来讲讲memset的时间戳优化数组清0。

什么是时间戳？
时间戳就是记录这是第几次调用树状数组的标志，在修改时如果发现当前的节点的时间戳不在当前时间就提前清零，如果询问时发现当前的节点的时间戳不在当前时间显然需要忽视这个节点，这样的操作类似于一种lazy思想——当修改时才清除当前节点。

这样的话在多次需要树状数组时就可以减少大量的不必要操作，起到十分显著的优化效果。——————CHN_JZ

int T;//时间戳
int time[N];//储存节点的访问时间
ll c[N];int n;
inline int lowbit(int x){return x & (-x);}
ll ask(int x){
    ll ans = 0;
    while(x){
        ans += (time[x]<T?0:c[x]);
        x -= lowbit(x);
    }
    return ans;
}
void add(int x,int y){
    for(;x <= n;x += lowbit(x)) {c[x] = time[x] < T?y:c[x] + y;time[x] = T;}
}

完整代码

int T;//时间戳
int time[N];//储存节点的访问时间
ll c[N];int n;
inline int lowbit(int x){return x & (-x);}
ll ask(int x){
    ll ans = 0;
    while(x){
        ans += (time[x]<T?0:c[x]);
        x -= lowbit(x);
    }
    return ans;
}
void add(int x,int y){
    for(;x <= n;x += lowbit(x)) {c[x] = time[x] < T?y:c[x] + y;time[x] = T;}
}
int a[N],b[N];
int main(){
    while(scanf("%d",&n) == 1&&n){
        T ++;
        for(int i = 1;i <= n;++i) scanf("%d",&a[i]),b[i] = a[i];
        sort(b + 1,b + n + 1);
        int m = unique(b+1,b+n+1) - b - 1;
        for(int i = 1;i <= n;++i) a[i] = lower_bound(b+1,b+m+1,a[i]) - b;
        ll ans = 0;
        for(int i = n;i >= 1;i --){
            ans += ask(a[i]-1);
            add(a[i],1);
        }
        printf("%lld\n",ans);
    }
}

有点尴尬的是不知道为什么这样反而慢了几十ms？应该是远古oj太破了吧。。。

Codeforces Round #624 (Div. 3)F
题意：
有 $n$ 个点在 $X$ 轴上，初始坐标值分别为 $a_1,....a_n$ ，然后每个点都有一个速度 $v_i$ ，定义 $d(i,j)$ 是经过 $t$ 秒后，两个点的最小距离。让你求 $\sum\limits_{1<=i<j<=n}^{n}d(i,j)$ 。

思路：
我们考虑对答案的贡献。显然对于 $x_i,x_j$ ，不失一般性设 $x_i<x_j$ ，如果 $v_i>v_j$ ，的话两个点迟早会相遇，也就是 $d(i,j)=0$ ，只有 $v_i<=v_j$ ，才有有贡献，且贡献为 $x_j-x_i$ 。
树状数组 +离散化
我们按 $a_i$ 从小到大排序，对每个点，我们只需要查询比 $a_i$ 的点且小于等于 $v_i$ 的点，那么答案的贡献是比他小的点的个数 $\cdot a_i-Sum$ ，其中 $Sum$ 为小于等于 $v_i$ 的 $a_i$ 的和值。

struct node{
    int a,b;
}res[N];
bool cmp(node A,node B){
    return A.a < B.a
}
int b[N];ll c[N][2];
int n;
void add(int x,int num){
    for(;x <= n;x += x&(-x)) c[x][0] ++,c[x][1] += num;
}
ll ask(int x,int k){
    ll ans = 0;
    while(x > 0){
        ans+= c[x][k];
        x -= x&(-x);
    }
    return ans;
}
int main(){
    n = read();
    rep(i,1,n) res[i].a = read();
    rep(i,1,n) b[i] = res[i].b = read();
    sort(res+1,res+n+1,cmp);
    sort(b+1,b+n+1);
    int m = unique(b+1,b+n+1) - b - 1;
    ll ans = 0;
    rep(i,1,n){
        int x = lower_bound(b + 1,b +m + 1,res[i].b) - b;
        ans += res[i].a*ask(x,0) - ask(x,1);
        add(x,res[i].a);
    }
    cout << ans;
}

poj2352
题意：在一个二维坐标系中存在着若干点，一个点的等级是这个点左下角点的数目。问你从 $0$ 到 $n-1$ 级分别有多少个点。
思路：
这显然是个二维偏序，我们固定 $y$ 轴，按 $x$ 轴查询。即先按 $y$ 从小到大排序（ $y$ 相同按 $x$ 轴从小到大排序），然后按照上面题目的思路，先查询，在插入。
注意：树状数组下标从1开始，所以对于可能出现不合法的情况可以偏移坐标轴。

struct node{
    int x,y;
}res[N];
bool cmp(node A,node B){
    if(A.y!=B.y) return A.y < B.y;
    else return A.x < B.x;
}
int c[N];int n;
inline int lowbit(int x) {return x & (-x);}
int ask(int x){
    int ans = 0;
    while(x){
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}
void add(int x,int y){
    for(;x <= N;x += lowbit(x)) c[x] += y;
}
int ans[N];
int main(){
    n = read();
    rep(i,1,n) res[i].x = read()+1,res[i].y = read();
    sort(res + 1,res + n +1,cmp);
    rep(i,1,n){
        ans[ask(res[i].x)] ++;
        add(res[i].x,1);
    }
    rep(i,0,n-1) printf("%d\n",ans[i]);
}

P1138 第k小整数

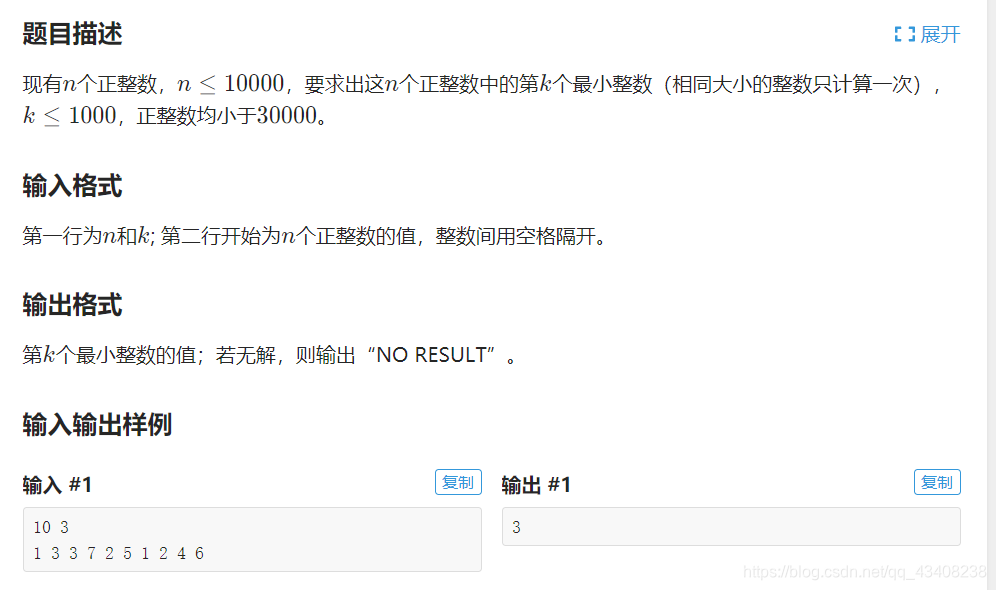
在这里插入图片描述
注意：这道题目重复的数不算排名，所以对于每一种数，我们只插入一次就好。直接看代码吧。

int c[N];
int m;
void add(int x,int y){
    for(;x <= m;x += x & (-x)) c[x] += y;
}
int ask(int x){
    int sum = 0;
    while(x){
        sum += c[x];
        x -= x&(-x);
    }
    return sum;
}
int a[N],b[N];
int kth(int x){//倍增求第k小
    int t = 0;
    for(int i = 19;i>=0;-- i){
        t += 1<<i;
        if(t>m||c[t]>=x) t -= 1<<i;
        else x -= c[t];
    }
    return b[t+1];
}
int main(){
    int n = read(),k = read();
    rep(i,1,n) a[i] = b[i] = read();

    sort(b+1,b+n+1);//离散化
    m = unique(b+1,b+n+1) - b - 1;

    rep(i,1,m) add(i,1);
    if(ask(m)<k) puts("NO RESULT");//看总排名有多少
    else cout << kth(k);
}