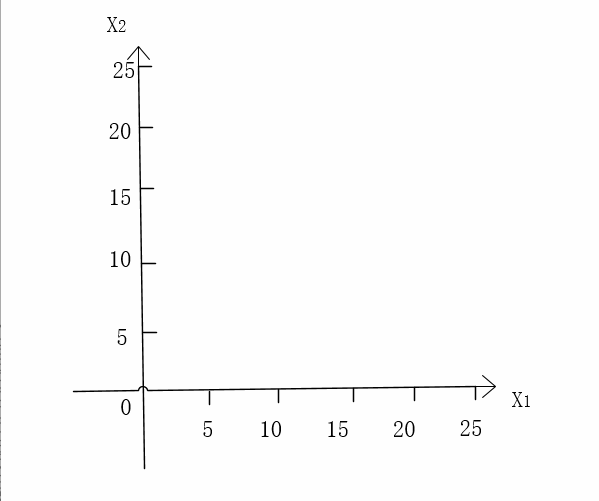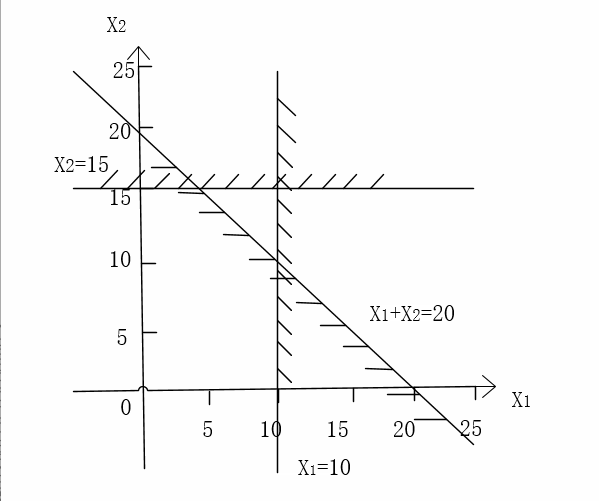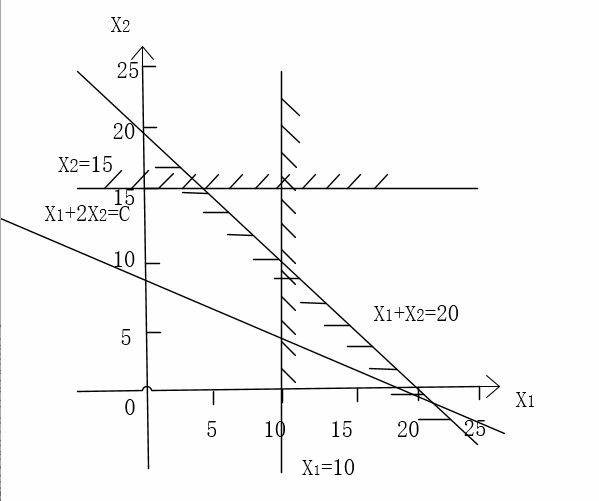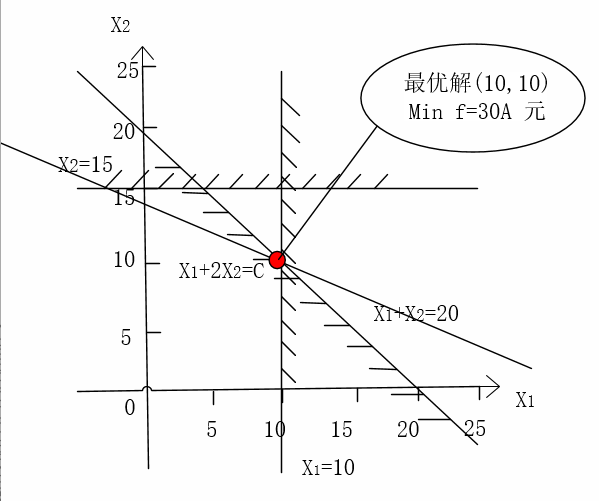《工程优化》1. 概论

《工程优化》1. 概论

1.数学模型标准形式

$\\ min　f(\vec{ｘ}) \\ 　　　　　　　　　ｓ.t. 　g_u(\vec{ｘ})\leq0　u=1,2,…,m \\　　　　　　　　　　　h_v(\vec{ｘ})=0　　v=1,2,…,n$

1. 数学模型三要素
   　* 　 $f(\vec{ｘ})$ ——————————————目标变量\评价函数
   　*　 $\vec{ｘ}$————————————————设计变量（又称决策变量）
   　 　 　　 $\vec{ｘ} =\lbrace x_1,x_2,…,x_n\rbrace^T$
   　*　 $g_u(\vec{ｘ}),h_v(\vec{ｘ})$————约束条件
   　*　说明：
   　　　(1) $\vec{ｘ}$是由坐标原点出发的矢量，端点表示一个设计点，所有设计点的集合——>设计空间。
   　　　(2) $x_i$为 $\vec{ｘ}$的第i个坐标轴的分量，各个 $x_i$之间相互独立。
   　　　(3)n——>维数（设计的自由度），考虑的设计变量不能太少，太少了能给出准确结果；考虑太多，不容易得出解。
   　　　(4)最优解： $x^*=\lbrace x_1^*,x_2^*,…,x_n^*\rbrace^T$
2. 数学模型分类
   　* 若u=0，v=0，即只有 $min_{x\in R}f(\vec{ｘ})$ ，为无约束优化问题，否则为约束优化问题。
   　* 若 $f(\vec{ｘ}),g_u(\vec{ｘ}),h_v(\vec{ｘ})$均为线性函数，则为线性规划问题，否则为非线性规划问题。

2.目标函数

• 一般形式： $f(\vec{ｘ})=f(x_1,x_2,…,x_n)$
  目标函数统一成 $min　f(\vec{ｘ})$;若为 $max　f(\vec{ｘ})$，也转换成最小值形式： $min　(-f(\vec{ｘ}))$
• 定义：从评价一个方案的优劣的系统各项性能指标中选出一个或者多个指标作为可行决策方案的最优性判据，称为目标函数，又称为评价函数。用 $f(\vec{ｘ})$表示，是设计变量 $x_i(i=1,2,…,n)$的函数。
• 目标函数的等值线: $f(\vec{ｘ})=C_i　(i=1,2,…)$
  　　(1)等值线表示了 $f(\vec{ｘ})$的变化情况（函数的性态），越内层的函数值越小，越外层的函数值越大；等值线稠密的地方函数值变化越快，反之变化较慢（原因：min）;
  　　(2)不同的等值线（面）不相交;
  　　(3)一般在 $x^*$附近等值线（面）呈近似的同心椭圆（球）族，其中心是最优解 $x^*$.
• 目标函数的判据
  　　(1)最小二乘法判据： $f(\vec{ｘ})= \sum_{i=1}^M W_i|e_i(x)|^2$
  　1到M所有采样点上性能函数与设计规范的误差平方加权值作为极小化判据。
  　　(2)极大极小化判据： $f(\vec{ｘ})= \max_{1\leq i\leq M}(W_i|e_i(x)|)$
  　对于每个可能的x值，在M个采样点中找出最大的加权绝对值误差值为极小化依据。
  　　(3)最小P乘判据： $f(\vec{ｘ})= \lbrace \sum_{i=1}^M W_i|e_i(x)|^p\rbrace^\frac {1} {p}　p=2,4,6,…$
  　弥补了极大极小判据 $f(\vec{ｘ})$不可微分的缺点。最小P乘判据可微，且当P趋于无限大时，最小P乘判据就变形为极大极小判据。

2.目标函数

• 定义：对设计变量取值所加的限制条件
• 表达形式：
  $\begin{cases} 不等式约束　g_u(x)\geq0　u=1,2,…,m\\ 等式约束　　h_v(x)=0 　v=1,2,…,p<n\end{cases}$
• 约束形式：
  $\begin{cases} 性能约束：设计变量必须满足的某些设计性能的要求。\\　　　　　如功率、KVL等。(又称为隐式约束) \\边界约束：设计变量变得上下限(又称显式约束) \\　　　　　a_i\leq x_i\leq b_i\end{cases}$
• 约束条件的几何意义：
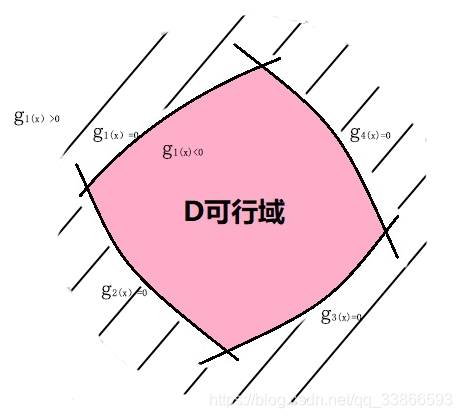
  　（1） $g_u(x)=0　u=1,2,…,m$-------约束线（面，超曲面），则将解空间分割成两部分： $g_u(x)< 0(可行域) 和g_u(x)> 0(不可行域，在图中用斜线阴影表示)$，可行域中点为可行解，不可行域中的点为不可行解
  　最终所有的m个可行域的交组成了可行域D。
  
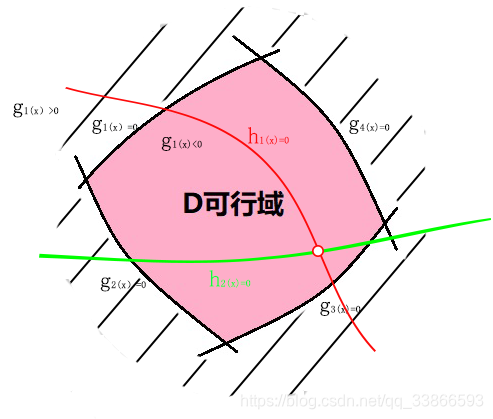
  　（2） $h_1(x)=0$可行域由一个面变成了这个面和 $h_1(x)=0$这条线的交集，即一条曲线段，多条等式约束最后产生唯一的可行点，就没有最好最坏区分。所以等式约束的个数p<n(该例子中n=2，p=2,有唯一解；当p=3时，没有交点时就会无解）
  
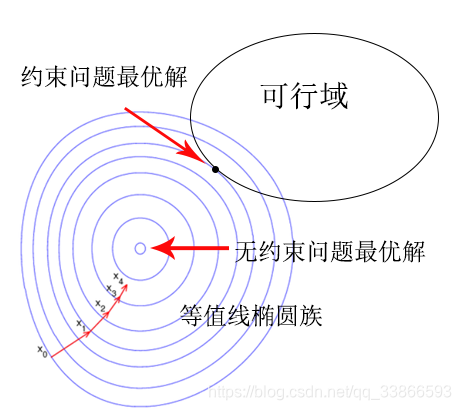
• 最优化问题的几何解释：
  等值线和可行域相切的点就是约束问题的最优解；等值线最小点为无约束问题最优解
  

3.优化问题分类

• 按照有无约束分为有约束优化问题和无约束优化问题
• 按照优化目标个数分为单目标优化问题和多目标优化问题
• 按照目标函数、约束条件是否为线性分为线性与非线性优化问题
• 连续的与离散的优化问题
  在离散优化问题里边有比较重要的一类问题：整数规划（即只能取整数0，1，2…），整数规划问题中又有0-1规划
• 网络最优化问题　　如电网规划，物流规划，生产工序

例

  两个发电站的输出功率分别是 $P_1$ kw和 $P_2$ kw，两电站可利用的最大功率 $P_{max}$=10kw，发电的费用为A元/kw和2A元/kw，负荷用量为20kw。问满足用电需要，两电站的店里如何分配使发电的总费用最小？
解：
（1）建立模型
决策变量： $x_1,x_2$ 即 $\vec{ｘ} =\lbrace x_1,x_2\rbrace^T$
目标函数： $minf(x_1,x_2)=A\cdot x_1+2A\cdot x_2$  
约束条件： $x_1\leq10$;  $x_2\leq 15$;  $x_1+x_2\geq 20$
（2）画坐标轴，用几何意义解题

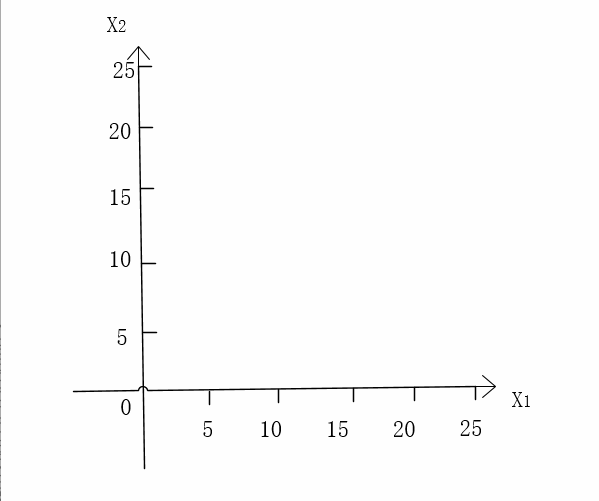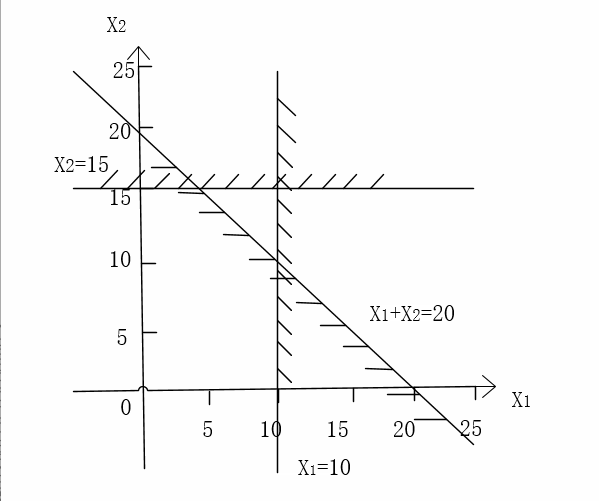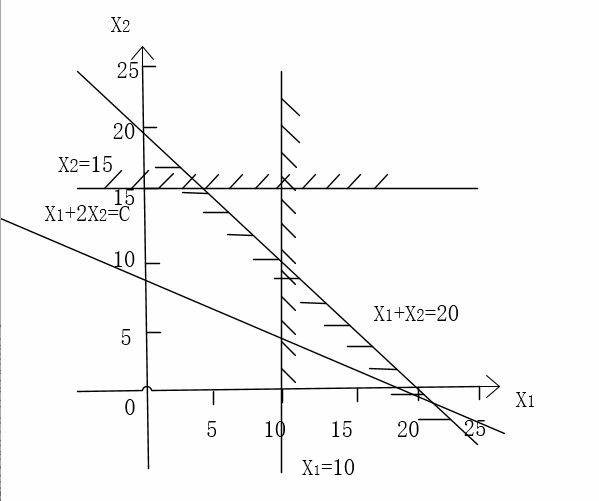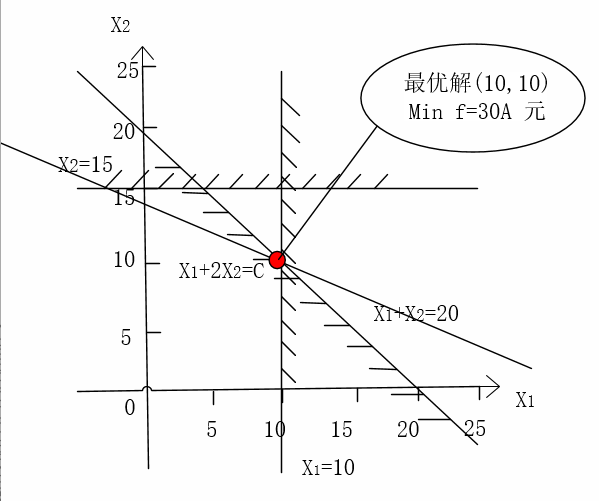
所以诸多工程优化问题是建立在多元函数的极值理论基础上的。