Orthogonal Convolutional Neural Networks

Wang J, Chen Y, Chakraborty R, et al. Orthogonal Convolutional Neural Networks.[J]. arXiv: Computer Vision and Pattern Recognition, 2019.

@article{wang2019orthogonal,
title={Orthogonal Convolutional Neural Networks.},
author={Wang, Jiayun and Chen, Yubei and Chakraborty, Rudrasis and Yu, Stella X},
journal={arXiv: Computer Vision and Pattern Recognition},
year={2019}}

概

本文提出了一种正交化CNN的方法.

主要内容

符号说明

\(X \in \mathbb{R}^{N \times C \times H \times W}\): 输入
\(K \in \mathbb{R}^{M \times C \times k \times k}\): 卷积核
\(Y \in \mathbb{R}^{N \times M \times H' \times W'}\): 输出

\[Y= Conv(K,X) \]

\(Y=Conv(K,X)\)的俩种表示

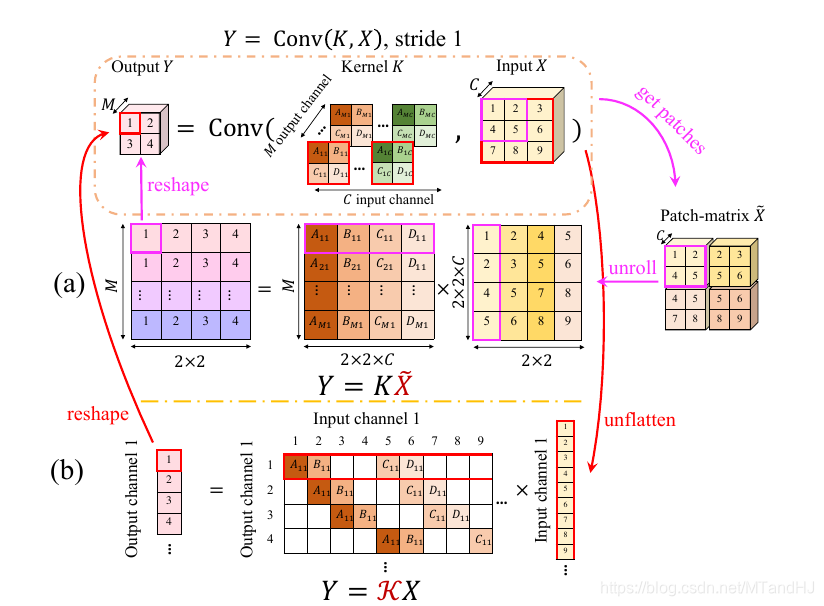
\(Y=K\tilde{X}\)

此时\(K\in \mathbb{R}^{M \times Ck^2}\), 每一行相当于一个卷积核, \(\tilde{X} \in \mathbb{R}^{Ck^2 \times H'W'}\), \(Y \in \mathbb{R}^{M \times H'W'}\).

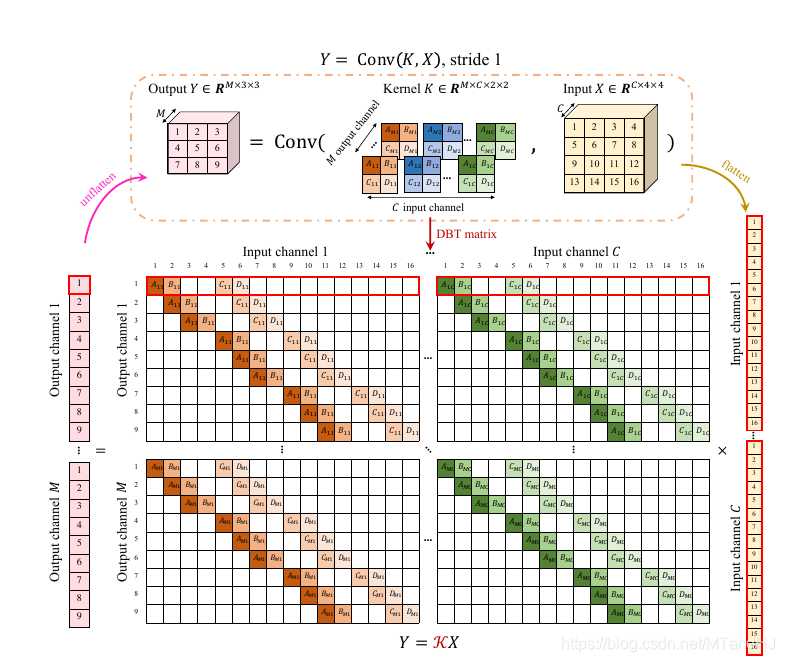
\(Y=\mathcal{K}X\)

此时\(X \in \mathbb{R}^{CHW}\)相当于将一张图片拉成条, \(\mathcal{K} \in \mathbb{R}^{MHW' \times CHW}\), 同样每一次行列作内积相当于一次卷积操作, \(Y \in \mathbb{R}^{MH'W'}\).

kernel orthogonal regularization

相当于要求\(KK^T=I\)(行正交) 或者\(K^TK=I\)(列正交), 正则项为

\[L_{korth-row}= \|KK^T-I\|_F,\\ L_{korth-col}= \|K^TK-I\|_F. \]

作者在最新的论文版本中说明了, 这二者是等价的.

orthogonal convolution

作者期望的便是\(\mathcal{K}\mathcal{K}^T=I\)或者\(\mathcal{K}^T\mathcal{K}=I\).

用\(\mathcal{K}(ihw,\cdot)\)表示第\((i-1) H'W'+(h-1)W'+w\)行, 对应的\(\mathcal{K}(\cdot, ihw)\)表示\((i-1) HW+(h-1)W+w\)列.

则\(\mathcal{K}\mathcal{K}^T=I\)等价于

\[\tag{5} \langle \mathcal{K}(ih_1w_1, \cdot), \mathcal{K}(jh_2w_2,\cdot)\rangle = \left \{ \begin{array}{ll} 1, & (i,h_1,w_1)=(j,h_2,w_2) \\ 0, & else. \end{array} \right. \]

\(\mathcal{K}^T\mathcal{K}=I\)等价于

\[\tag{10} \langle \mathcal{K}(\cdot, ih_1w_1), \mathcal{K}(\cdot, jh_2w_2)\rangle = \left \{ \begin{array}{ll} 1, & (i,h_1,w_1)=(j,h_2,w_2) \\ 0, & else. \end{array} \right. \]

实际上这么作是由很多冗余的, 可以进一步化为更简单的形式.
(5)等价于

\[\tag{7} Conv(K, K,padding=P, stride=S)=I_{r0}, \]

其中\(I_{r0}\in \mathbb{R}^{M\times M \times (2P/S+1) \times (2P/S+1)}\)仅在\([i,i,\lfloor \frac{k-1}{S} \rfloor+1,\lfloor \frac{k-1}{S} \rfloor+1], i=1,\ldots, M\)处为\(1\)其余元素均为\(0\).

\[P= \lfloor \frac{k-1}{S} \rfloor \cdot S. \]

其推导过程如下(这个实在不好写清楚):

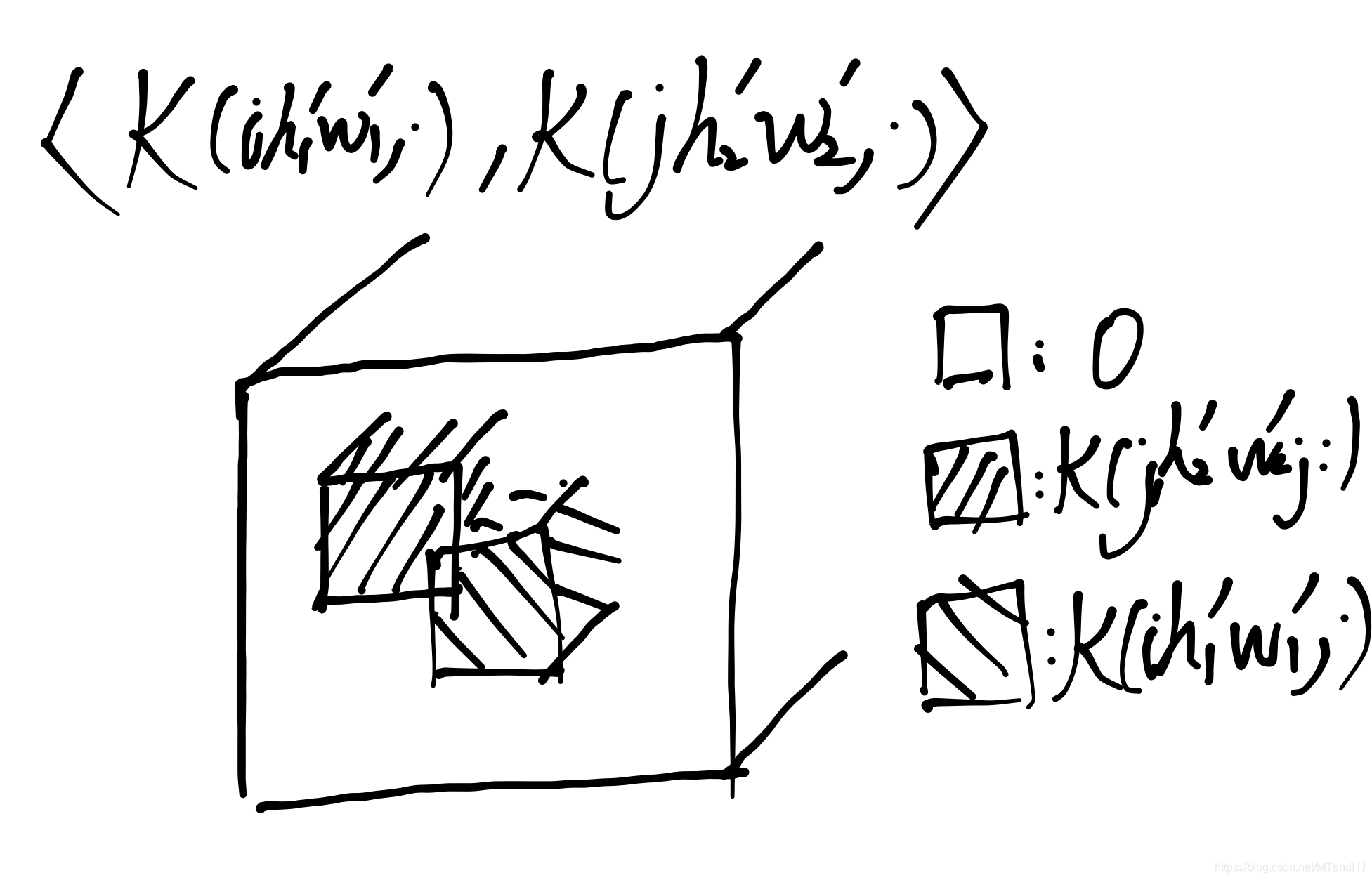
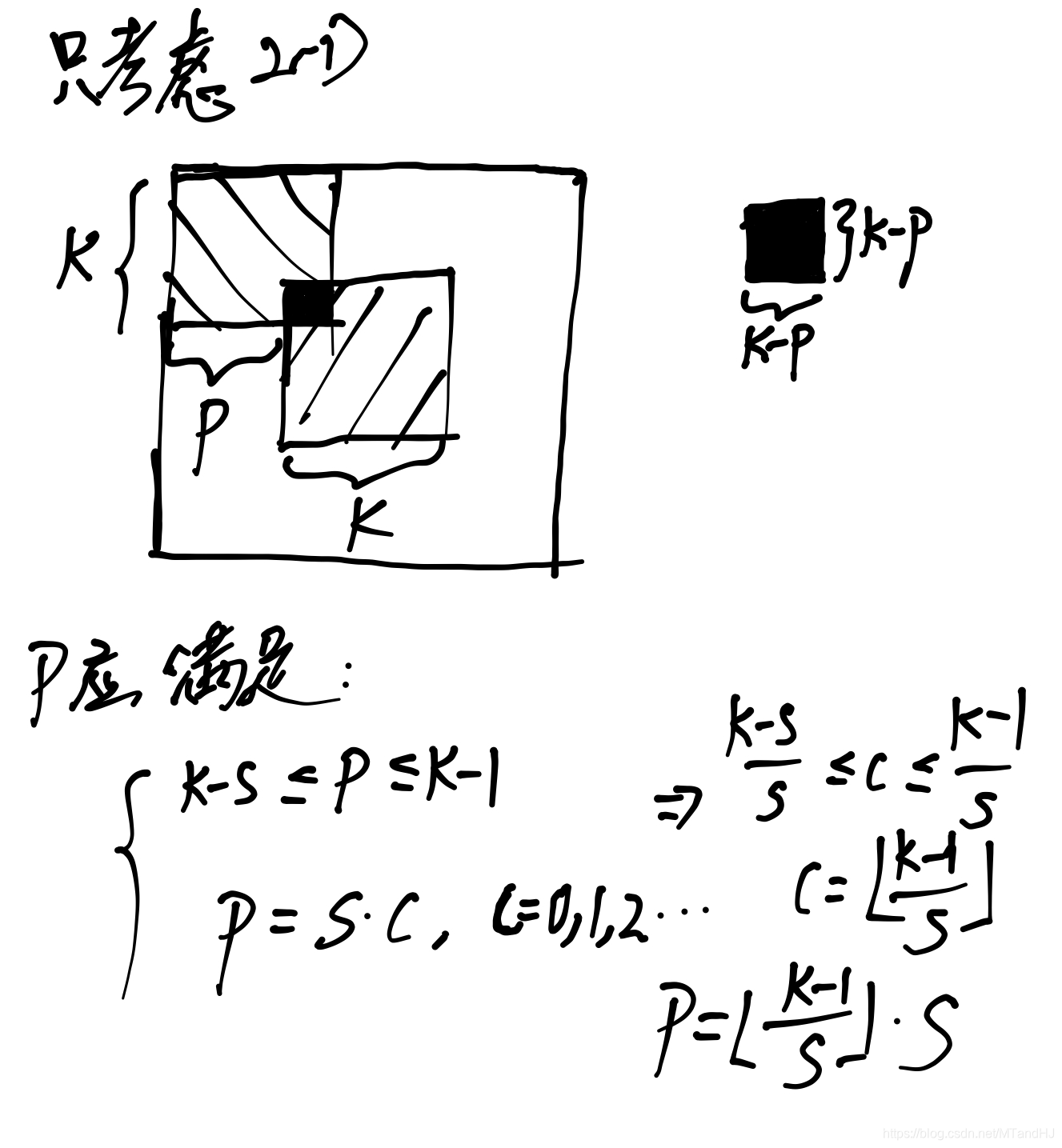
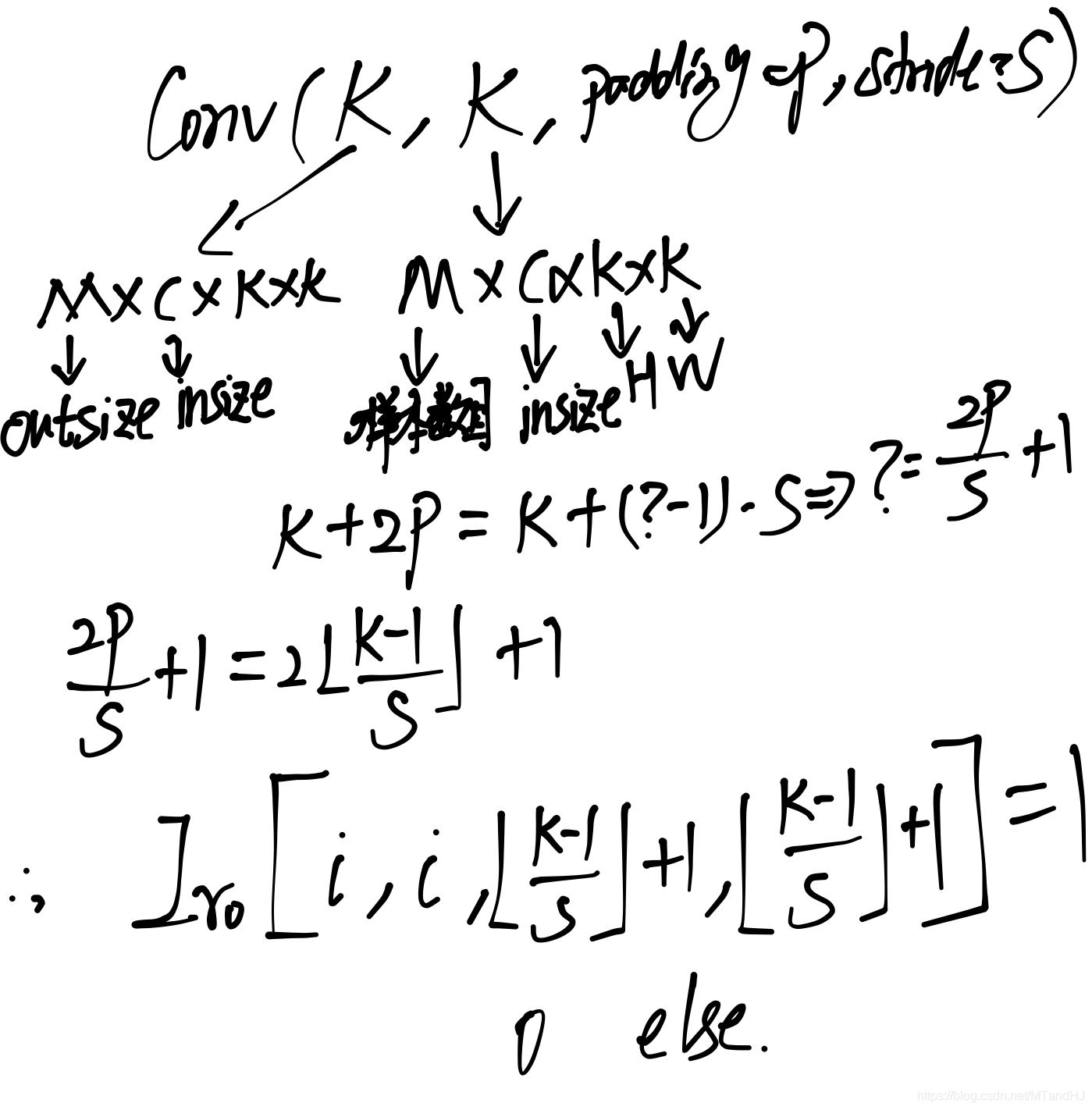
\(\mathcal{K}^T\mathcal{K}\)在\(S=1\)特殊情况下的特殊情况下, (10)等价于

\[\tag{11} Conv (K^T,K^T, padding=k-1, stride=1)=I_{c0}, \]

其中\(I_{c0} \in \mathbb{R}^{C \times C \times (2k-1) \times (2k-1)}\), 同样仅在\((i,i,k,k)\)处为1, 其余非零.\(K^T \in \mathbb{R}^{C \times M \times k \times k}\)是\(K\)的第1, 2坐标轴进行变换.

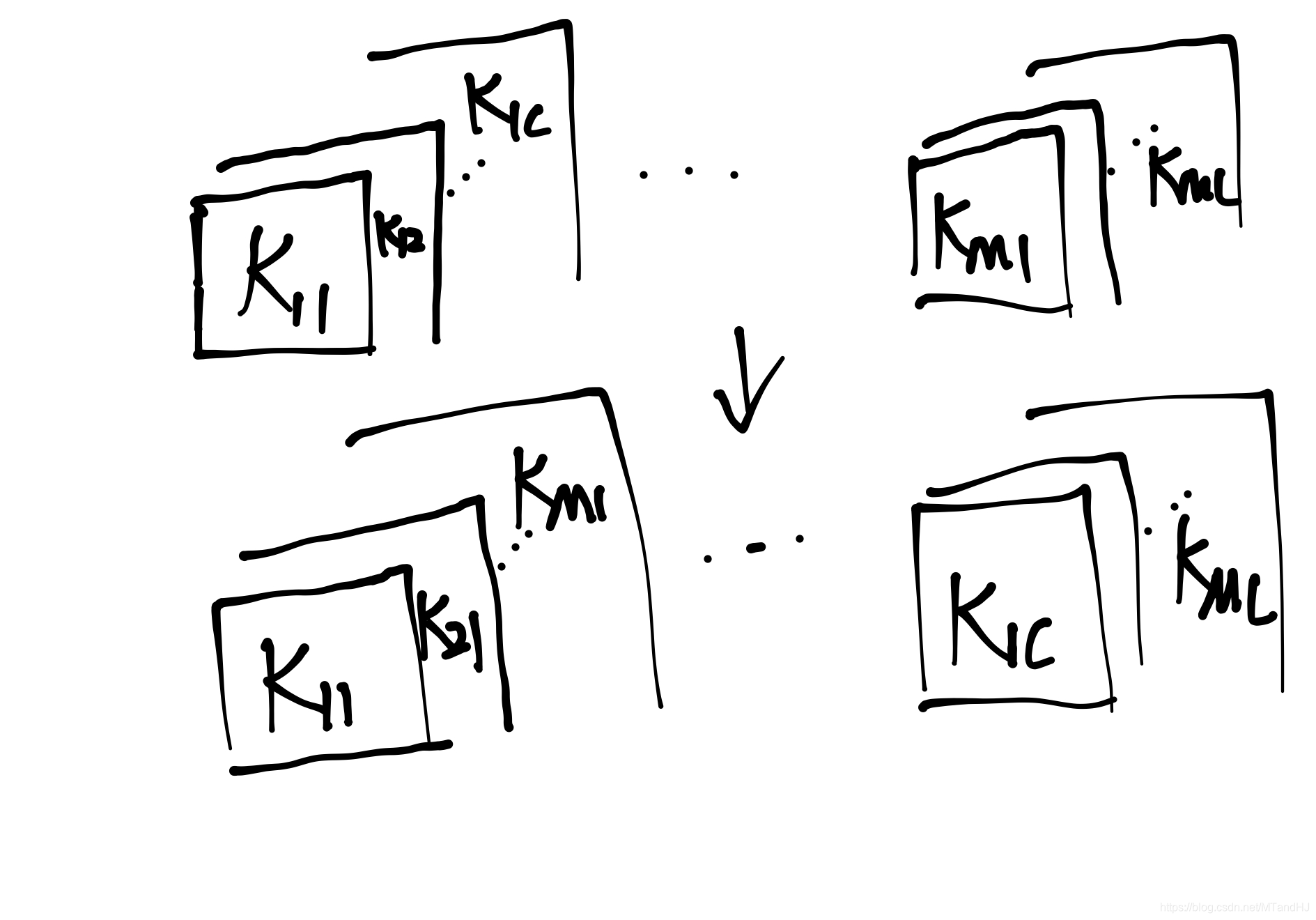
同样的

\[\min_K \|\mathcal{K}\mathcal{K}^T-I\|_F \]

与

\[\min_K \|\mathcal{K}^T\mathcal{K}-I\|_F \]

是等价的.

另一方面, 最开始提到的kernel orthogonal regularization是orthogonal convolution的必要条件(但不充分)\(KK^T=I\), \(K^TK=I\)分别等价于:

\[Conv(K,K,padding=0)=I_{r0} \\ Conv(K^T, K^T, padding=0)=I_{c_0}, \]

其中\(I_{r0} \in \mathbb{R}^{M \times M \times 1 \times 1}\), \(I_{c0} \in \mathbb{R}^{C \times C \times 1 \times 1}\).