更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016
更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016
因子分析就是从研究对象中寻找公共因子的方法。
判别分析、聚类分析、因子分析的比较:
对面来了来了一群女生,我们一眼就能分辨出谁美谁丑,这是判别分析;并且在我们脑海里会对这群女生聚为两类:美的一类和丑的一类,这是聚类分析;我们之所以认为某个女孩漂亮是因为她具有漂亮女孩所具有的一些共同点,比如漂亮的脸蛋、高挑的身材等等,这种从研究对象中寻找公共因子的办法就是因子分析。
因子分析也是利用降维思维,把每一个原始变量分解成两部分,一部分是少数几个公共因子的线性组合,另一部分是该变量所独有的特殊因子,其中公共因子和特殊因子都是不可观测的隐变量,我们需要对公共因子做出具有实际意义的合理解释。
1.因子分析简介
1.1 基本因子分析模型
设p维总体x=(x1,x2,....,xp)'的均值为u=(u1,u2,....,u3)',因子分析的一般模型为
x1=u1+a11f1+a12f2+........+a1mfm+ε1
x2=u2+a21f1+a22f2+........+a2mfm+ε2
.........
.. . . .
xp=up+ap1f1+fp2f2+..........+apmfm+εp
其中,f1,f2,.....,fm为m个公共因子;εi是变量xi(i=1,2,.....,p)所独有的特殊因子,他们都是不可观测的隐变量。称aij(i=1,2,.....,p;j=1,2,.....,m)为变量xi的公共因子fi上的载荷,它反映了公共因子对变量的重要程度,对解释公共因子具有重要的作用。上式可以写为矩阵形式
x=u+Af+ε
其中A=(aij)pxm 称为因子载荷矩阵;f=(f1,f2,....,fm)'为公共因子向量;ε=(ε1,ε2,.....εp)称为特殊因子向量
1.2 共性方差与特殊方差
xi的方差var(xi)由两部分组成,一个是公共因子对xi方差的贡献,称为共性方差;一个是特殊因子对xi方差的贡献,称为特殊方差。每个原始变量的方差都被分成了共性方差和特殊方差两部分。
1.3 因子旋转
因子分析的主要目的是对公共因子给出符合实际意义的合理解释,解释的依据就是因子载荷阵的个列元素的取值。当因子载荷阵某一列上各元素的绝对值差距较大时,并且绝对值大的元素较少时,则该公共因子就易于解释,反之,公共因子的解释就比较困难。此时可以考虑对因子和因子载荷进行旋转(例如正交旋转),使得旋转后的因子载荷阵的各列元素的绝对值尽可能量两极分化,这样就使得因子的解释变得容易。
因子旋转方法有正交旋转和斜交旋转两种,这里只介绍一种普遍使用的正交旋转法:最大方差旋转。这种旋转方法的目的是使因子载荷阵每列上的各元素的绝对值(或平方值)尽可能地向两极分化,即少数元素的绝对值(或平方值)取尽可能大的值,而其他元素尽量接近于0.
1.4 因子得分
在对公共因子做出合理解释后,有时还需要求出各观测所对应的各个公共因子的得分,就比如我们知道某个女孩是一个美女,可能很多人更关心该给她的脸蛋、身材等各打多少分,常用的求因子得分的方法有加权最小二乘法和回归法。
注意:因子载荷矩阵和得分矩阵的区别:
因子载荷矩阵是各个原始变量的因子表达式的系数,表达提取的公因子对原始变量的影响程度。因子得分矩阵表示各项指标变量与提取的公因子之间的关系,在某一公因子上得分高,表明该指标与该公因子之间关系越密切。简单说,通过因子载荷矩阵可以得到原始指标变量的线性组合,如X1=a11*F1+a12*F2+a13*F3,其中X1为指标变量1,a11、a12、a13分别为与变量X1在同一行的因子载荷,F1、F2、F3分别为提取的公因子;通过因子得分矩阵可以得到公因子的线性组合,如F1=a11*X1+a21*X2+a31*X3,字母代表的意义同上。
1.5 因子分析中的Heywood(海伍德)现象
如果x的各个分量都已经标准化了,则其方差=1。即共性方差与特殊方差的和为1。也就是说共性方差与特殊方差均大于0,并且小于1。但在实际进行参数估计的时候,共性方差的估计可能会等于或超过1,如果等于1,就称之为海伍德现象,如果超过1,称之为超海伍德线性。超海伍德现象意味着某些特殊因子的方差为负,表明肯定存在问题。造成这种现象的可能原因包括:
共性方差本身估计的问题;
太多的共性因子,出现了过拟合;
太少的共性因子,造成拟合不足;
数据太少,不能提供稳定的估计;
因子模型不适合这些数据。
当出现海伍德现象或超海伍德现象时,应对估计结果保持谨慎态度。可以尝试增加数据量,或改变公共因子数目,让公共因子数目在一个允许的范围内变动,观察估计结果是否有改观;还可以尝试用其他多元统计方法进行分析,比如主成分析。
2. 因子分析的MATLAB函数
MATLAB提供了factoran函数来进行因子分析。
factoran函数用来根据原始样本观测数据、样本协方差矩阵和样本相关系数矩阵,计算因子模型总的因子载荷矩阵A的最大似然估计,求特殊方差的估计、因子旋转矩阵和因子得分,还能对因子模型进行检验。factoran函数的调用格式如下:
<1>lambda=factoran(X,m)
返回包含m个公共因子模型的载荷矩阵lambda。输出参数X是n行d列的矩阵,每行对应一个观测,每列对应一个变量。m是一个正整数,表示模型中公共因子的个数。输出参数lambda是一个d行m列的矩阵,第i行第j列元素表示第i个变量在第j个公共因子上的载荷。
<2>[lambda,psi]=factoran(X,m)
返回特殊方差的最大似然估计psi,psi是包含d个元素的列向量,分别对应d个特殊方差的最大似然估计。
<3>[lambda,psi,T]=factoran(X,m)
返回m行m列的旋转矩阵T
<4>[lambda,psi,T,stats]=factoran(X,m)
返回一个包含模型检验信息的结构体变量stats,模型检验的原假设是H0:因子数=m。输出参数stats包括4个字段,其中stats.loglike表示对数似然的最大值,stats.def表示误差自由度,stats,chisq表示近似卡方检验统计量,stats.p表示检验的p值。对于给定的显著性水平a,若检验的p值大于显著性水平a,则接受原假设H0,说明用含有m个公共因子的模型拟合原始数据是合适的,否则,拒绝原假设,说明拟合是不合适的。
<5>[lambda,psi,stats,F]=factoran(X,m)
返回因子得分矩阵F。F是一个n行m列的矩阵,每一行对应一个观测的m个公共因子的得分。如果X是一个协方差矩阵或相关系数矩阵,则factoran函数不能及时因子得分。factoran函数用相同的旋转矩阵计算载荷阵lambda和因子得分F。
<6> [.......]=factoran(.....,param1,val1,param2,val2,.......)
允许用户指定可选的成对出现的参数名和参数值,用来控制模型的拟合和输出,可用的参数名与参数值如下:
| 参数名 |
参数值 |
说明 |
| ‘xtype’ |
指定输出参数X的类型 |
|
| ‘data’ |
原始数据(默认情况) |
|
| ‘covariance’ |
正定的协方差矩阵或相关系数矩阵 |
|
| ‘scores’ |
预测因子得分方法。若X不是原始数据,‘score’将被忽略 |
|
| ‘wls’‘Bartlett’ |
加权最小二乘估计(默认情况) |
|
| ‘regression’‘Thomson’ |
最小均方误差法,相当于岭回归 |
|
| ‘start’ |
最大似然估计中特殊方差psi的最初值 |
|
| ‘random’ |
选取d个在[0 1]区间上服从均匀分布的随机数 |
|
| ‘Rsquared’ |
用一个尺度因子乘以diag(inv(corrcoef(X)))作为初始点(默认情况) |
|
| 正整数 |
指定最大似然法拟合的次数 |
|
| 矩阵 |
用矩阵指定最大似然法的初始点 |
|
| ‘rotate’ |
指定因子载荷矩阵和因子得分矩阵的旋转方法 |
|
| ‘none’ |
不进行旋转 |
|
| ‘equamax’ |
Orthomax旋转的特殊情况 |
|
| ‘orthomax’ |
最大方差旋转法 |
|
| ‘parsimax’ |
Orthomax旋转的一个特殊情况(默认) |
|
| ‘pattern’ |
执行斜交旋转(默认)或正交旋转 |
|
| ‘procrustes’ |
执行斜交旋转(默认)或正交旋转 |
|
| ‘promax’ |
执行一次斜交procrustes旋转 |
|
| ‘quartimax’ |
Orthomax旋转的一个特殊情况 |
|
| Varimax |
Orthomax旋转的以特殊情况 |
|
| 函数句柄 |
用户自定义的旋转函数的句柄 |
|
| ‘coeff’ |
一个介于0-1之间的数 |
不同的值对应不同的orthomax旋转 |
| ‘normalize’ |
‘on’或1 ‘off’或0 |
若为‘on’或1,(默认),单位化 ‘off’或0,不进行单位化 |
| ‘reltol’ |
正标量 |
指定‘orthomax’或‘varimax’的收敛容限 |
| ‘maxit’ |
正整数 |
指定‘orthomax’或‘varimax’的最大迭代次数,默认250 |
| ‘target’ |
矩阵 |
指定‘orthomax’旋转所必须的目标因子载荷阵 |
| ‘type’ |
‘oblique’或 ‘orthogonal’ |
指定‘procrustes’旋转的类型,默认‘oblique’ |
| ‘power’ |
大于或等于1的变量 |
指定‘promax’旋转中生成目标矩阵的幂指数,默认值是4 |
| ‘userargs’ |
自定义旋转的额外参数 |
一个标记开始位置的参数 |
| ‘nobs’ |
正整数 |
指定实际观测的个数 |
| ‘delta’ |
[0,1)内的标量 |
设定最大似然估计中特殊方差 psi 的下界,默认0.005 |
| ‘qptimopts’ |
由命令statset(‘factoran’)生成的结构体变量 |
指定用来计算最大似然估计的迭代算法的控制参数 |
3.基于样本观测值矩阵的因子分析
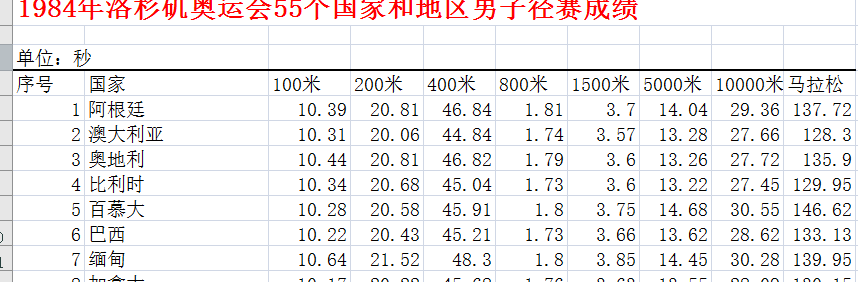
下表列出了奥运会上55个国家和地区男子径赛的成绩数据。
%读取数据
[X,textdata] = xlsread('径赛成绩.xls');%读取数据
X = X(:,3:end); %提取X的第3至最后一列,即要分析的数据
varname = textdata(4,3:end);%提取textdata的第4行,第3至最后一列,即变量名
obsname = textdata(5:end,2);%提取textdata的第2列,第5行至最后一行,即国家名或地区名
(1)4个公共因子
%调用factoran函数根据原始观测数据作因子分析
% 从原始数据)出发,进行因子分析,公共因子数为4
% 进行因子旋转(最大方差旋转法)
[lambda,psi,T,stats] = factoran(X,4)
%计算贡献率,因子载荷矩阵的列元素的平方和除以维数
Contribut = 100*sum(lambda.^2)/8
CumCont = cumsum(Contribut) %计算累积贡献率
lambda =
0.2786 0.9537 0.0229 -0.0115
0.3857 0.8530 0.1155 0.0794
0.5339 0.7211 0.2231 0.0133
0.6679 0.5884 0.3984 0.0271
0.7852 0.5020 0.2316 0.2177
0.8963 0.3866 0.0919 0.0441
0.9076 0.3966 0.0722 0.0276
0.9132 0.2759 0.0889 -0.0473
psi =
0.0122
0.1040
0.1449
0.0484
0.0305
0.0368
0.0130
0.0797
T =
0.7359 0.6640 0.1248 0.0450
0.6576 -0.7471 0.0762 0.0600
-0.1612 -0.0180 0.9055 0.3921
0.0102 -0.0240 0.3984 -0.9169
stats =
loglike: -0.0159
dfe: 2
chisq: 0.7600
p: 0.6839
Contribut =
50.4392 39.2256 3.7195 0.7459
CumCont =
50.4392 89.6648 93.3843 94.1303
结果分析:
从因子载荷矩阵的估计lambda来看,前2列个元素的取值差距较大,也就是说前2个因子易于解释,而后2列元素取值都比较小,后两个因子很难给出合理的解释。
从特殊方差矩阵的估计psi来看,各变量的特殊方差都比较小, 并没有出现海伍德现象,这说明4因子模型的拟合效果非常好。
从模型检验信息stats来看,检验的p值为0.6830>0.05,说明在显示性水平0.05下接受原假设,原假设是H0:m=4,也就是说用4个公共因子的因子模型拟合原始数据是比较合适的。
从贡献率Contribut和累积贡献率CumCont来看,前2个因子对原始数据总方差的贡献率分别为50.4392和39.2256,累积贡献率达到了89.6648%,这说明因子模型中公共因子的数目还可以进一步减少,只考虑2个公共因子应该是比较合适的。
(2)2个公共因子
% 从原始数据出发,进行因子分析,公共因子数为2% 进行因子旋转(最大方差旋转法)
[lambda,psi,T,stats,F] = factoran(X, 2)
Contribut = 100*sum(lambda.^2)/8 %计算贡献率
CumCont = cumsum(Contribut) %计算累积功效率
%为了显示直观,定义元胞数组,以元胞数组形式显示因子载荷阵
[varname' num2cell(lambda)]
lambda =
0.2876 0.9145
0.3790 0.8835
0.5405 0.7460
0.6891 0.6244
0.7967 0.5324
0.8993 0.3968
0.9058 0.4019
0.9138 0.2809
psi =
0.0810
0.0758
0.1514
0.1353
0.0817
0.0338
0.0180
0.0860
T =
0.8460 0.5331
-0.5331 0.8460
stats =
loglike: -0.3327
dfe: 13
chisq: 16.3593
p: 0.2303
F =
0.3559 -0.2915
-0.4780 -0.8471
-0.7700 0.2096
-0.8101 -0.2296
1.5513 -1.2863
0.1130 -0.9439
0.4870 0.6517
-0.1077 -0.9427
0.1283 -0.3221
-0.0807 0.3137
-0.6971 0.4201
2.1491 3.8666
-0.7703 2.0418
-0.3658 -0.3744
-0.5524 -0.0057
2.2451 -1.6206
-0.8307 -0.0362
-0.2249 -1.0027
-0.5469 -0.9058
-0.4472 -0.9495
-0.5690 -1.0585
0.3541 -0.6699
-0.1484 1.7113
-0.1908 -0.4946
-0.4443 0.6125
1.1054 0.2773
-0.9685 0.5613
-0.3487 0.6141
-0.1339 -1.5855
-0.7194 0.0366
-1.0005 -0.0460
0.2728 -0.2344
-0.4679 1.7101
0.1439 -0.2381
1.6495 -0.9003
0.8386 1.7727
-0.8522 0.5704
-0.9430 0.2815
-1.0196 0.3119
-1.0439 0.6911
0.9329 1.1914
0.8011 0.5121
-0.2759 -0.9260
-1.3163 0.8694
-0.8484 0.2215
1.9305 -0.5694
-0.7851 0.0249
-0.4985 -0.4038
-0.6000 -0.3152
0.3723 0.2694
2.3334 -0.8775
-0.8423 1.1545
-0.1616 -1.8243
-0.2886 -1.2890
3.3842 0.2935
Contribut =
51.1556 40.5565
CumCont =
51.1556 91.7121
ans =
'100米' [0.2876] [0.9145]
'200米' [0.3790] [0.8835]
'400米' [0.5405] [0.7460]
'800米' [0.6891] [0.6244]
'1500米' [0.7967] [0.5324]
'5000米' [0.8993] [0.3968]
'10000米' [0.9058] [0.4019]
'马拉松' [0.9138] [0.2809]
结果分析:
从此时的因子载荷阵的估计lambda来看,5000m,10000m和马拉松的成绩在第1个公共因子的载荷比较大,说明第1个公共因子反映的是人的耐力,可解释为耐力因子;100m和200m的成绩在第2个公共因子上的载荷比较大,说明第2个公共因子反映的是人的速度,可解释为速度因子。两个因子对原始数据总方差的贡献率分别为51.1556%和40.5565%,累积贡献率达到了91.7121%。
从特殊方差矩阵的估计psi来看,个变量的特殊方差也都比较小,只有400m和800m的成绩对应的特殊方差超过了0.1,并没有出现海伍德现象,这说明2因子模型的拟合效果是非常好的。
从模型检验信息stats来看,检验的p值为0.2303>0.05,可知在显著性水平0.05下接受原假设,原假设H0:m=2,也就是说用2个公共因子的因子模型拟合原始数据是合适的。
(3)因子得分
下面将因子得分F分别按耐力因子得分和速度因子得分进行排序,以便分析各个国家或地区在径赛项目上的优势。
%将因子得分F分别按耐力因子得分和速度因子得分进行排序
obsF = [obsname, num2cell(F)] %将国家和地区名与因子得分刚在一个元胞数组中显示
F1 = sortrows(obsF, 2) ; % 按耐力因子得分排序
F2 = sortrows(obsF, 3); % 按速度因子得分排序
head = {'国家/地区','耐力因子','速度因子'};
result1 = [head; F1]
result2 = [head; F2]
因为数据较多,先不显示,然后做出因子得分的散点图。
从因子得分的取值可以看出,速度优势越明显的国家或地区,其速度因子得分值越小。耐力优势越明显的地区,其耐力因子得分值越小,因此用因子得分的负值做出散点图,从散点图上可以看出各个国家和地区在径赛上的优势。
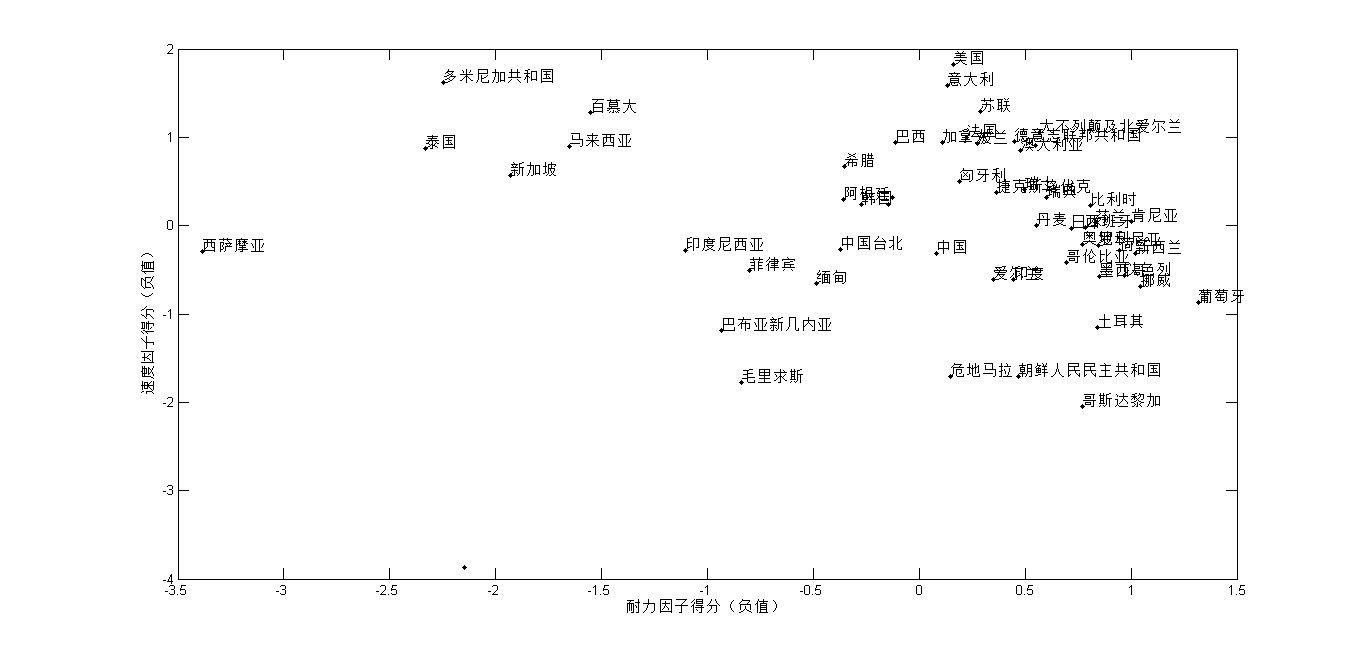
%绘制因子得分负值的散点图
plot(-F(:,1),-F(:,2),'k.');%作因子
xlabel('耐力因子得分(负值)');
ylabel('速度因子得分(负值)');
gname(obsname);%交互式添加各散点的标注
从图中可以看出,葡萄牙人耐力优势明显,美国人和多米尼亚和意大利人速度优势明显,中国人总体实力居中,耐力和速度都不占优势。
更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016