树链剖分主要用来维护树的路径信息,大致思路是把一棵树变成一个特定的序列,将树上的问题转化成线性结构上的问题,然后用数据结构维护在这个序列
引例:
树链剖分的思想与本例类似
有一棵n个节点的有根树,每个节点都有一个权值
一共有m次更新/查询
更新:将节点x的权值修改为y
查询:查询x以节点为根的子树中所有节点的权值和
众所周知,对一棵树进行dfs,然后按照dfs访问的顺序把可以所有节点排成一个序列,那么这个序列当中,每一棵子树都是连续的一段,因为dfs从开始访问一棵子树到结束对这棵子树的访问期间绝对不会访问这棵子树以外的任何节点
只要按照dfs顺序把所有节点排成一列,然后用一个树状数组维护它,那么每棵子树都对应着树状数组的一个区间。只要我们可以记录每棵子树对应的区间,对节点的修改就可以转化为对树状数组的单点更新,对子树的查询就可以转换为对树状数组的区间查询。
至于如何记录每棵子树的区间,其实只需要记录每个节点v的dfs序(即节点v在树状数组内的位置)dfn[v]和它的子树的大小size[v]即可。这样的话它对应的区间就等于[dfn[v],dfn[v]+size[v])
接下来就是正题
树链剖分
其实吧,树链剖分这个名字听着挺高端,实际上和刚才那个例子思路一样,只不过树链剖分不仅要让每棵子树的节点在一个区间内,还要让这个序列更有利于树上路径信息的维护
仔细想想,一个随随便便dfs出来的序列,除了所有子树一定是连续的一段以外,其实很多树上的路径也是“比较连续”的,毕竟dfs的特点就是一条道走到黑
那么即便不去树链剖分,只是随随便便dfs一下,也可使得路径“比较连续” 比如下图
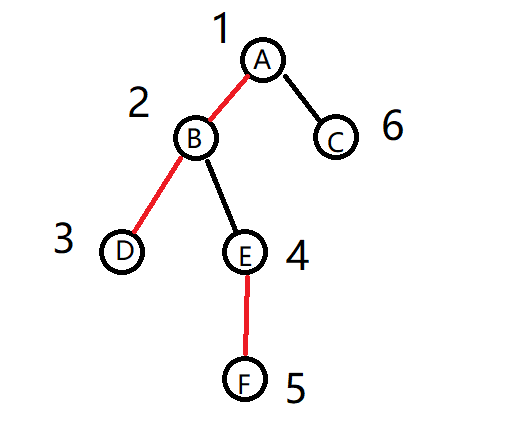
数字代表dfs的顺序
每个节点的子树遍历顺序是按照图中的从左到右顺序进行的
dfs序列:ABDEFC
红边代表在dfs序列中连续的边 如AB在dfs序列中相邻,称为重边,黑边称为轻边
AB在dfs序列中连续,所以<A,B>是重边,AC不相邻,所以<A,C>是轻边
重边组成的链叫重链
每个节点由重边连接的儿子称为 重儿子,其余的叫轻儿子 如B的重儿子是D
显然,每个节点(除叶子节点外)有且只有一个重儿子
每个节点(除叶子节点外)在dfs序列中的下一个节点就是它的重儿子
这样的话,如果要查询D到C路径上的点权和,则只需要将D~A(由于ABD在dfs序列上是连续的,直接用线段树/树状数组的查询功能即可)的点权和与A~C的点权和相加即可,而不需要把路径上所有的点遍历一遍
树链剖分差不多就是这个功能,其实随随便便dfs一遍就可以实现,没必要搞什么树链剖分
完
这样就完了吗?那这种情况怎么办?
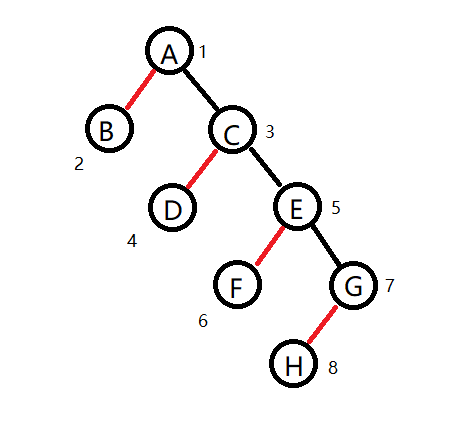
由于某些原因,很多节点下面的重链太短,这样就会导致对树上路径的实际的查询过程几乎是一个一个地查找,效率十分低下
解决方案其实很简单,看看上面那个被零零散散的红边割得稀碎的树就知道了
直接把ACEGH作为重链,不就好了吗
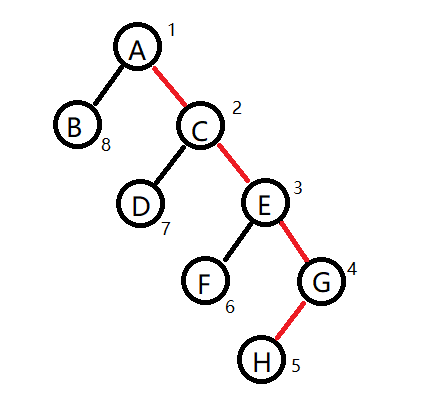
那么,对于一棵一般的树,如何为每个非叶子节点选择重儿子呢?
答案是哪个儿子的子树最大,就选哪个
这样可以保证任意一条树上的路径都可以拆成O(log n)条重链片段
为什么?
沿着树上的边向上走,显然,当前节点的size一定单调递增
如果向上走的过程中跨越了一条轻边,就意味着从一条重链跳到了另外一条重链

以这个图为例,由于hson[A]=B,可知size[C]<=size[B]
size[A]=size[B]+size[C]+1
也就是说
size[A]>2*size[C]
每跨越一次轻边,当前节点的size至少变成原来的两倍
则经历的重链数量为O(log n)
线段树/树状数组区间查询的时间复杂度是O(log n),所以查询整条路径的时间复杂度是O((log n)2)
这个时间复杂度虽然看上去没那么好,但其实已经很快了
以上就是树链剖分的大致思路与时间复杂度的粗略证明,但很多细节还要通过代码来理解
接下来就是代码
首先是一堆变量
int cnt,dfp;//cnt 边的数量 dfp dfs计数器 edge e[N*2];//N*2条边 int head[N],fa[N],hson[N],dfn[N],size[N],top[N],depth[N]; int val[N],segv[N];//val 点权值 segv 线段树维护的序列 SegTree tree; //线段树 //head 邻接链表头节点 //fa 父节点 //hson 重儿子 //dfn dfs序//size 子树大小 //top top[i]表示i所在重链的链顶 //depth 节点所在深度
树链剖分需要两遍dfs,第一遍是预处理,计算出每个子树的大小size,每个节点的深度depth,每个非叶子节点的重儿子hson
第二遍dfs就是“正式dfs”计算出dfs序列以及每个节点所在的重链的链顶top
void dfs1(int x,int f=-1,int dep=1) { size[x]=1; fa[x]=f; int maxsize=0; depth[x]=dep++; for (int i=head[x];i!=-1;i=e[i].next) { int y=e[i].to; if (y==f) continue; dfs1(y,x,dep); size[x]+=size[y]; if (maxsize<size[y]) maxsize=size[y],hson[x]=y; } } void dfs2(int x,int ctp) { dfn[x]=++dfp; segv[dfp]=val[x]; top[x]=ctp; if (hson[x]!=-1) dfs2(hson[x],ctp); for (int i=head[x];i!=-1;i=e[i].next) { int u=e[i].to; if (u==hson[x] || u==fa[x]) continue; dfs2(u,u); } }
树链剖分函数
void slpf(int root) { dfp=0; dfs1(root); dfs2(root,root); tree.build(segv,1,n); }
查询路径
int queryPath(int x,int y) { int res=0; while (top[x]!=top[y])//循环 直到x和y在同一条重链上 { if(depth[top[x]]<depth[top[y]]) std::swap(x,y);//保持x是链顶较深的那一个 即depth[top[x]]>=depth[top[y]] res+=tree.query(dfn[top[x]],dfn[x],1,n);//结果+=x到x链顶的权重和 x=fa[top[x]]; }
//循环结束后,x与y一定在同一条重链上 if (depth[x]>depth[y]) std::swap(x,y);//令y是较深的那一个 res+=tree.query(dfn[x],dfn[y],1,n);//结果+=最后一段 return res%mod; } void updatePath(int x,int y,int v)//与queryPath同理,就不注释了(好吧,其实是因为懒得写了) {
while (top[x]!=top[y]) { if(depth[top[x]]<depth[top[y]]) std::swap(x,y); tree.update(dfn[top[x]],dfn[x],v,1,n); x=fa[top[x]]; } if (depth[x]>depth[y]) std::swap(x,y); tree.update(dfn[x],dfn[y],v,1,n); }
整体代码来一波
struct edge { int from,to,next; edge() { next=-1; } edge(int fr,int tu,int nxt) { from=fr; to=tu; next=nxt; } }; struct Graph { int cnt,dfp; edge e[N*2]; int head[N],fa[N],hson[N],dfn[N],size[N],top[N],depth[N]; int val[N],segv[N]; SegTree tree; Graph() { cnt=0; memset(head,-1,sizeof(head)); memset(fa,-1,sizeof(fa)); memset(hson,-1,sizeof(hson)); memset(dfn,-1,sizeof(dfn)); } void addEdge(int x,int y) { e[++cnt]=edge(x,y,head[x]); head[x]=cnt; } void dfs1(int x,int f=-1,int dep=1) { size[x]=1; fa[x]=f; int maxsize=0; depth[x]=dep++; for (int i=head[x];i!=-1;i=e[i].next) { int y=e[i].to; if (y==f) continue; dfs1(y,x,dep); size[x]+=size[y]; if (maxsize<size[y]) maxsize=size[y],hson[x]=y; } } void dfs2(int x,int ctp) { dfn[x]=++dfp; segv[dfp]=val[x]; top[x]=ctp; if (hson[x]!=-1) dfs2(hson[x],ctp); for (int i=head[x];i!=-1;i=e[i].next) { int u=e[i].to; if (u==hson[x] || u==fa[x]) continue; dfs2(u,u); } } void slpf(int root) { dfp=0; dfs1(root); dfs2(root,root); tree.build(segv,1,n); } int queryPath(int x,int y) { int res=0; while (top[x]!=top[y])//循环 直到x和y在同一条重链上 { if(depth[top[x]]<depth[top[y]]) std::swap(x,y);//保持x是链顶较深的那一个 即depth[top[x]]>=depth[top[y]] res+=tree.query(dfn[top[x]],dfn[x],1,n);//结果+=x到x链顶的权重和 x=fa[top[x]]; } //循环结束后,x与y一定在同一条重链上 if (depth[x]>depth[y]) std::swap(x,y);//令y是较深的那一个 res+=tree.query(dfn[x],dfn[y],1,n);//结果+=最后一段 return res; } void updatePath(int x,int y,int v)//与queryPath同理,就不注释了(好吧,其实是因为懒得写了) { while (top[x]!=top[y]) { if(depth[top[x]]<depth[top[y]]) std::swap(x,y); tree.update(dfn[top[x]],dfn[x],v,1,n); x=fa[top[x]]; } if (depth[x]>depth[y]) std::swap(x,y); tree.update(dfn[x],dfn[y],v,1,n); } int queryTree(int x) { return tree.query(dfn[x],dfn[x]+size[x]-1,1,n); } void updateTree(int x,int v) { tree.update(dfn[x],dfn[x]+size[x]-1,v,1,n); } };