Reference:
Pisinger, D. (1999). Linear Time Algorithms for Knapsack Problems with Bounded Weights. Journal of Algorithms, 33(1), 1–14.
差不多是带着自己理解的翻译吧,并不是完全按照论文顺序来的
~ 引入 ~
动态规划中,有一个经典的问题是子集和(Subset-sum Problem, SSP):
给定$n$个物品,每个物品的重量是$w_i$,从中选出一些物品使得它们的总重量为$C$,问有多少种取法
这显然可以使用$O(nC)$的01背包解决
那么考虑将问题稍微改变一下,变为有重量限制的子集和:
给定$n$个物品,每个物品的重量是$w_i$,从中选出一些物品使他们的总重量不超过$C$,问最大的总重量是多少
这好像没啥区别嘛,照样是一个$O(nC)$的01背包就能解决
如果我们令$W=max\{w_i\}$,则一般有$nW>C$(否则答案直接就是$\sum w_i$),那么也可以认为这个DP的复杂度是$O(n^2W)$
而这篇论文提出的 平衡(balancing) 的技巧,可以将求解这个问题优化到$O(nW)$
~ 平衡的一些概念 ~
我们用$x=(x_1,x_2,...,x_n)$来表示一个解,其中$x_i \in \{0,1\}$表示选择第$i$种物品的数量
考虑从第一件物品开始贪心地选择,直到选到第$b$件物品时$\sum_{i=1}^{b}w_i>C$
我们称这个解为截断解(break solution)$x'$:当$i<b$时$x_i=1$,当$b\leq i\leq n$时$x_i=0$
定义1:
平衡解(balanced solution)可以通过如下方式获得
1. 截断解$x'$是一个平衡解
2. 对平衡解$x$进行平衡插入(balanced insert):若平衡解$x$满足$\sum_{i=1}^{n}w_ix_i\leq C$(总重量不大于$C$),我们选择一个$t\geq b$将$x_t=0$变成$x_t=1$,那么改变后的解仍为平衡解
3. 对平衡解$x$进行平衡删除(balanced remove):若平衡解$x$满足$\sum_{i=1}^{n}w_ix_i>C$(总重量大于$C$),我们选择一个$s<b$将$x_s=1$变成$x_s=0$,那么改变后的解仍为平衡解
也就是说,我们可以从截断解$x'$出发,通过不断进行平衡插入/平衡删除操作,能构造出很多很多平衡解;而这些平衡解的总重量是有范围的
性质1:
对于任意平衡解$x$,均有$C-W+1\leq \sum_{i=1}^{n}w_ix_i \leq C+W$
这是因为,我们只能对总重量不大于$C$的平衡解进行平衡插入,那么总重量最多变成$C+W$;同理,我们只能对总重量大于$C$的平衡解进行平衡删除,那么总重量最少也是$C-W+1$
不过需要区分的是,并不是总重量在$[C-W+1,C+W]$之间的解均为平衡解,因为平衡插入与平衡删除对原先的总重量是有要求的
命题1:
有重量限制的子集和问题中,最优解一定是平衡解
证明:设最优解为$x^*$,那么我们将所有$1\leq i<b$中$x^*_i\neq x'_i$(即$x^*_i=0,x'_i=1$)的$i$拿出来,记为$s_1,...,s_\alpha$;将所有$b\leq i\leq n$中$x^*_i\neq x'_i$(即$x^*_i=1,x'_i=0$)的$i$拿出来,记为$t_1,...,t_\beta$
那么我们从截断解$x'$出发,若总重量不超过$C$则依次添加$t_1,...,t_\beta$,若总重量超过$C$则依次删去$s_1,...,s_\alpha$,最终就能得到$x*$
(论文中证明了好大一段,感觉没有说出什么其他的东西)
~ 解决有重量限制的子集和问题 ~
直接做这个问题还是不太行的,我们不妨定义一个子问题:
记$f_{s,t}(c)$表示,必选第$1$到第$s-1$件物品、可选第$s$到第$t$件物品时,在总重量不超过$c$时能够选出的最大重量,即
\[f_{s,t}(c)=max\{\sum_{i=1}^{s-1}w_i+\sum_{i=s}^{t}w_ix_i\leq c\}\]
同时要求$x_i=\left\{\begin{array}{**lr**} 1, & i<s\\ \{0,1\}, & s\leq i\leq t\end{array}\right.$是一个平衡解
那么我们可以用一个三元组$(s,t,\mu)$代表一个状态,其中$\mu=f_{s,t}(\mu)$,即$\mu$为恰能被选出的某个重量
我们需要用各种已有状态来更新信息,而其中一些状态是无用的
定义2:
假如有两个状态$(s,t,\mu)$和$(s',t',\mu')$,且$\mu=\mu'$而$s\geq s',t\leq t'$,那么$(s',t',\mu')$是一个无用状态
可以这样理解这个定义:状态$(s',t',\mu')$比$(s,t,\mu)$具有更高的自由度,即可选的位置更多;在这种情况下,我们既然可以用较小的自由度选出$\mu$,那么就没有必要扩大选择的范围了
于是对于固定的$t,\mu$,我们只需要记录最大的$s$对应的状态即可
记$s_t(\mu)$表示,可选物品的右边界是$t$、需要选出的重量为$\mu$时,最大的可选物品左边界
即$s_t(\mu)=max\{s| f_{s,t}(\mu)=\mu\}$
规定当某个重量$w$暂时不能被选出的时候,$s_t(w)=0$
我们用$s_t(\mu)$来解决问题!
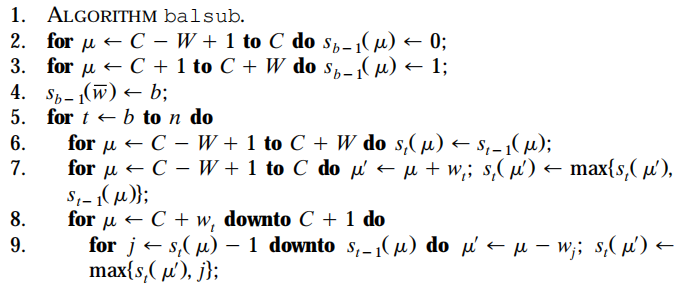
先从头开始解读一下正确性,时间复杂度的证明之后再讨论
第2、3行中,给$s_{b-1}(\mu)$赋初值;第2行还好理解,第3行的用意可以暂时先不管
第4行中,$\overline{w}$表示的是截断解$x'$对应的重量,即$\overline{w}=\sum_{i=1}^{n} w_ix'_i$;而$s_{b-1}(\overline{w})\leftarrow b$就表示,我们必须全选物品$1$到$b-1$才能得到$\overline{w}$,那么可选物品的最大左边界是$b$
由第5行开始进入循环,按$t$从小到大依次将$s_t(\mu)$全部计算出;我们不妨以$t=b$、即第一轮循环为例
第6行用$s_{t-1}(\mu)$给$s_t(\mu)$赋初值;这是好理解的,因为不选第$t$件物品时就是$t-1$的情况
第7行中,我们尝试对所有总重量小于等于$C$的平衡解进行平衡插入,加入的物品是第$t$件,那么$\mu'=\mu+w_t$就是平衡插入后的总质量;也就是说,我们在必选第$1...s_{t-1}(\mu)-1$件物品、可选第$s_{t-1}(\mu)...t$件物品时,可以选出$\mu'$的总重量,故用$s_{t-1}(\mu)$尝试更新$s_t(\mu')$
第8行中,我们尝试对所有总重量大于$C$的平衡解进行平衡删除,删除的物品由第9行枚举
第9行中,对于$\mu$的总重量,其必选物品的范围是$1...s_t(\mu)-1$,我们考虑从这些必选物品中退一个(如果退的是可选物品,那么这个方案必然在之前被计算到过,否则该物品就不会在“可选”范围内);如果想要退掉物品$j$,那么平衡删除后的总重量就是$\mu'=\mu-w_j$,也就是说我们在必选第$1...j-1$件物品、可选第$j...t$件物品时,可以选出$\mu'$的总重量,故用$j$尝试更新$s_t(\mu')$
不过还需要解释为什么是从$s_t(\mu)-1$枚举到$s_{t-1}(\mu)$而不是枚举到$1$:进行平衡删除而导致的更新一定需要在当前轮选择第$t$件物品,否则会在之前某轮已用相同的值更新过了$\mu'$(因为不选第$t$件物品的所有状态一定在$t-1$时全部更新过了);而枚举到$j<s_{t-1}(\mu)$时,表示可以全选第$1...s_{t-1}(\mu)-1$件物品、可选第$s_{t-1}(\mu)...t-1$件物品而选出总重量$\mu$,那么在此时平衡删除第$j$件物品的方案可以不选第$t$件物品,也就是说不会对于$s_t(\mu-w_j)$产生更新
现在我们也可以理解第3行了:对于总重量大于$C$的平衡解,我们需要枚举要退的物品,在初始情况下需要一直退到$1$,故$\mu>C$时有$s_{b-1}(\mu)=1$
最后,有重量限制的子集和问题 答案就是满足$s_n(\mu)\neq 0,\mu\leq C$的最大的$\mu$
模板题:OpenCup 18290F ($Subset\ Sum$,
$XX\ Open\ Cup\ named\ after\ E.V.\ Pankratiev:\ Grand\ Prix\ of\ Bytedance$)
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=20005; int n,C,W; int w[N]; int s[2][2*N]; int main() { int T; scanf("%d",&T); while(T--) { for(int i=N-W+1;i<=N+W;i++) s[0][i]=s[1][i]=0; W=0; scanf("%d%d",&n,&C); for(int i=1;i<=n;i++) scanf("%d",&w[i]),W=max(W,w[i]); int sum=0,b=0; for(int i=1;i<=n && sum+w[i]<=C;i++) b=i,sum+=w[i]; ++b; if(b>n) { printf("%d\n",sum); continue; } for(int i=N-W+1;i<=N;i++) s[0][i]=0; for(int i=N+1;i<=N+W;i++) s[0][i]=1; s[0][N-C+sum]=b; int p=1; for(int i=b;i<=n;i++,p^=1) { for(int j=N-W+1;j<=N+W;j++) s[p][j]=s[p^1][j]; for(int j=N-W+1;j<=N;j++) s[p][j+w[i]]=max(s[p][j+w[i]],s[p^1][j]); for(int j=N+w[i];j>N;j--) for(int k=s[p][j]-1;k>=s[p^1][j];k--) s[p][j-w[k]]=max(s[p][j-w[k]],k); } for(int i=N;i>=N-W+1;i--) if(s[p^1][i]) { printf("%d\n",C+i-N); break; } } return 0; }
注意需要用滚动数组
(待续)