使用纯Python代码实现深层神经网络

引言

我们已经知道了深层神经网络的原理。今天就来实战一下，今天要做的事情像用逻辑回归实现图像识别一样，识别一个图像中有没有含有猫，不过用的是手写的深层神经网络。

我们已经在使用单隐藏层神经网络对平面数据分类中实现了两层的神经网络，本文看下如何实现深层的神经网络。

代码实现

我们先来实现一些辅助函数，后面会用到这些函数来实现深层神经网络，包括：

1. 参数初始化
2. 实现前向传播算法函数(包括下面四步)
   • 每层网络层的线性(LINEAR)部分，计算 $Z^{[l]}$
   • 实现激活(ACTIVATION)函数(relu/sigmoid)
   • 组合上面两步到一个新的[LINEAR->ACTIVATION]前向函数中(每层神经网络包括这两步)
   • 叠加上面的[LINEAR->ACTIVATION] $L-1$次，然后增加[LINEAR->SIGMOID]做为输出层
3. 计算损失
4. 实现反向传播算法函数(也包括四步，注意和前向传播算法相比顺序有什么区别于联系)
   • 实现反向传播中的线性部分
   • 实现激活函数的导数
   • 组合上面两步到一个新的[LINEAR->ACTIVATION]反向传播函数中
   • 叠加[LINEAR->RELU]反向传播 $L-1$次，增加[LINEAR->SIGMOID]反向传播到一个新的函数中
5. 最后更新参数

这些辅助函数实现了深层神经网络梯度下降更新参数的全过程。
整个过程如下图：

每个前向函数都对应一个反向函数，这就是下面看到的，为什么每步前向函数中都要缓存一些值。这些值可用于计算梯度。

现在按照上面的步骤一个个实现。

首先是激活函数及其导数：

def sigmoid(Z):
    """
    通过numpy实现sigmoid函数
    
    Arguments:
    Z -- 任何形状的numpy数组
    
    Returns:
    A --sigmoid(z)的值, 与Z的形状一致
    cache -- 同时返回入参Z,可用于反向传播中
    """
    
    A = 1/(1+np.exp(-Z))
    cache = Z
    
    return A, cache

def relu(Z):
    """
    实现RELU函数

    Arguments:
    Z -- 任何形状的numpy数组

    Returns:
    A -- relu(z)的值, 与Z的形状一致
    cache -- 同时返回入参Z,可用于反向传播中
    """
    
    A = np.maximum(0,Z)#relu函数
    
    cache = Z 
    return A, cache


def relu_backward(dA, cache):
    """
    实现RELU单元的反向传播(relu的导数)

    Arguments:
    dA -- 激活值的梯度
    cache -- 上面函数中保存的Z

    Returns:
    dZ -- Z的梯度
    """
    
    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.
    
    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0
        
    return dZ

def sigmoid_backward(dA, cache):
    """
    实现SIGMOID单元的反向传播(sigmoid的导数)

    Arguments:
    dA -- 激活值的梯度
    cache -- 上面函数中保存的Z

    Returns:
    dZ -- Z的梯度
    """
    
    Z = cache
    
    a = 1/(1+np.exp(-Z))
    dZ = dA * a * (1-a)
        
    return dZ

两层网络初始化

接下来实现初始化方法，先从两层的浅层网络开始，然后到 $L$层的深层网络。

两层网络的结构是： LINEAR -> RELU -> LINEAR -> SIGMOID.

def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- 输入层大小(神经元数)
    n_h -- 隐藏层大小
    n_y -- 输出层大小
    
    Returns:
    parameters --字典:
                    W1 -- (隐藏层)权重矩阵 (n_h, n_x)
                    b1 -- (隐藏层)偏差向量 (n_h, 1)
                    W2 -- (输出层)权重矩阵(n_y, n_h)
                    b2 -- (输出层)偏差向量 (n_y, 1)
    """
    
    np.random.seed(1)
    
    W1 = np.random.randn(n_h,n_x) * 0.01
    b1 = np.zeros((n_h,1))
    W2 = np.random.randn(n_y,n_h) * 0.01
    b2 = np.zeros((n_y,1))
    
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters    

L层网络初始化

$L$层网络的初始化更复杂，因为它有更多的权重矩阵和偏差向量。在初始化 $L$层网络时，要确保每层的维度。
$n^{[l]}$表示 $l$层的神经元数。

输入 $X$的形状是 $(12288,209)$， $209$是样本数量：

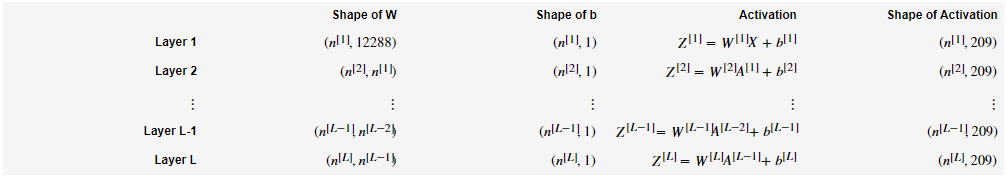
当在python中计算 $W X + b$ 时， $b$会按列复制3份变成 $3\times 3$的矩阵，比如：

$W = \begin{bmatrix} j & k & l\\ m & n & o \\ p & q & r \end{bmatrix}\;\;\; X = \begin{bmatrix} a & b & c\\ d & e & f \\ g & h & i \end{bmatrix} \;\;\; b =\begin{bmatrix} s \\ t \\ u \end{bmatrix}\tag{2}$

$WX + b$变成:

$WX + b = \begin{bmatrix} (ja + kd + lg) + s & (jb + ke + lh) + s & (jc + kf + li)+ s\\ (ma + nd + og) + t & (mb + ne + oh) + t & (mc + nf + oi) + t\\ (pa + qd + rg) + u & (pb + qe + rh) + u & (pc + qf + ri)+ u \end{bmatrix}\tag{3}$

$L$层网络的结构是 [LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID。即前面 $L-1$层用ReLU作为激活函数，接着是一个以SIGMOID激活函数的输出层

# 深层网络的参数初始化
def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- 每层维度列表，比如[4,2,1]表示输入层4个特征，隐藏层2个神经元，最后是一个单元的输出层
    
    Returns:
    parameters -- 返回包含参数 "W1", "b1", ..., "WL", "bL"的字典：
                    Wl --权重矩阵 (layer_dims[l], layer_dims[l-1])
                    bl --偏置向量 (layer_dims[l], 1)
    """
    
    np.random.seed(1)
    parameters = {}
    L = len(layer_dims)            # 网络的层数
    # 第0层表示输入层
    # 这里从1开始，到$L-1$
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1]) * 0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
        
    return parameters

接下来是前向传播算法的实现。

实现前向传播

我们先实现两个基本函数：

• LINEAR(线性计算)
• LINEAR -> ACTIVATION(RELU或SIGMOID).

最后实现一个函数包含整个模型的前向传播：

• [LINEAR -> RELU] $\times$ [(L-1) -> [LINEAR -> SIGMOID

线性计算可以用下面向量化的公式来计算：

$Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}\tag{4}$

这里 $A^{[0]} = X$.

def linear_forward(A_prev, W, b):
    """
    实现前向传播的线性计算部分

    Arguments:
    A_prev -- 前一层的激活值 (或输入数据) ：(前一层的单元数, 样本数)
    W -- 权重矩阵: (当前层单元数, 前一层单元数)
    b -- 偏置向量, (当前层单元数, 1)

    Returns:
    Z --  线性计算结果，激活函数的输入值，也称pre-activation参数
    cache -- 包含"A_prev", "W" 和 "b" 的字典
    """
    
    Z = np.dot(W,A_prev) + b
    
    cache = (A_prev, W, b)
    
    return Z, cache


def linear_activation_forward(A_prev, W, b, activation):
     """
    实现 LINEAR->ACTIVATION 层的前向传播

    Arguments:
    A_prev -- 前一层的激活值 (或输入值): (前一层的单元数, 样本数)
    W -- 权重矩阵: (当前层单元数, 前一层单元数)
    b -- 偏置向量, (当前层单元数, 1)
    activation -- 当前层使用的激活函数："sigmoid"或"relu"

    Returns:
    A -- 激活值，激活函数的输出值, 也称 the post-activation 值
    cache -- 一个包含 linear_cache 和 activation_cache 的元组
    """
    Z,linear_cache = linear_forward(A_prev,W,b) # Z,  (A_prev, W, b)

    if activation == "sigmoid":
        A,activation_cache = sigmoid(Z)# A,Z
    elif activation == "relu":
        A,activation_cache = relu(Z) #A,Z
    
    cache = (linear_cache, activation_cache)

    return A, cache # A ,((A_prev, W, b),Z)

为了实现深层网络的前向传播，需要进行 $L-1$次计算 [LINEAR -> RELU] 的过程，最后一层是[LINEAR -> SIGMOID]。

​
我们用AL 表示 $A^{[L]} = \sigma(Z^{[L]}) = \sigma(W^{[L]} A^{[L-1]} + b^{[L]})$.

def L_model_forward(X, parameters):
    """
    实现完整的前向传播过程 [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID]计算
    
    Arguments:
    X -- 输入数据, (输入大小, 样本数)
    parameters -- 初始化函数initialize_parameters_deep()的输出
    
    Returns:
    AL -- 最后一层激活值
    caches -- [(A_prev, W, b),Z]缓存列表:
               每个 linear_activation_forward()函数返回的缓存 (L-1个) 
    """
    L = len(parameters) // 2 #每一层都有两个参数(W和b)，除以2得到层数
    caches = []
    A_prev = X
    # 从1到L-1(L-2个)
    for l in range(1,L):
        A_prev,cache = linear_activation_forward(A_prev,parameters['W'+str(l)],parameters['b'+str(l)],'relu')
        caches.append(cache)
    # 最后一层的激活值
    AL,cache = linear_activation_forward(A_prev,parameters['W'+str(L)],parameters['b'+str(L)],'sigmoid')
    caches.append(cache) #共L-2 + 1 = L-1个
    
    return AL,caches

计算损失值

用下面的公式计算损失值 $J$: $-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right)) \tag{7}$

def compute_cost(AL, Y):
    """
    计算损失值

    Arguments:
    AL -- 最后一层的输出值(概率), shape (1, 样本数)
    Y -- 标签向量 (0:非猫,1:猫), shape (1, 样本数)

    Returns:
    cost -- 交叉熵损失值
    """
    
    m = Y.shape[1] #样本数
    # 实现公式即可
    cost = -1.0 * np.sum((Y * np.log(AL) + (1-Y) * np.log(1 - AL))) / m
    
    cost = np.squeeze(cost) # 确保是个标量
    
    return cost

​
计算好了损失值后就可以实现反向传播了。

实现反向传播

和前向传播一样，我们先实现反向传播的基本函数：

• LINEAR 反向传播
• [LINEAR -> ACTIVATION] 反向传播，ACTIVATION是激活函数的导数

最后实现一个函数包含整个模型的反向传播：

• [LINEAR -> RELU] $\times$ (L-1) -> [LINEAR -> SIGMOID] 反向传播
  
  上面的 $L$表示损失值。

每层 $l$的线性部分: $Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}$

首先通过 $dZ^{[l]} = \frac{\partial \mathcal{L} }{\partial Z^{[l]}} = dA^{[l]} g^{[l]\prime}(Z^{[l]})$来计算 $dZ^{[l]}$

然后计算 $(dW^{[l]}, db^{[l]}, dA^{[l-1]})$.

上面的三个输出 $(dW^{[l]}, db^{[l]}, dA^{[l-1]})$是通过输入 $dZ^{[l]}$计算的，下面是我们要用到的公式：
$dW^{[l]} = \frac{\partial \mathcal{J} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T} \tag{8}$
$db^{[l]} = \frac{\partial \mathcal{J} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}\tag{9}$
$dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]} \tag{10}$

上面通过relu_backward和sigmoid_backward实现了 $dZ^{[l]}$

def linear_backward(dZ, cache):
    """
    实现l层反向传播中线性部分

    Arguments:
    dZ -- 当前层线性部分输出的梯度
    cache --元组 (A_prev, W, b) ，当前层前向传播时计算的linear_cache

    Returns:
    dA_prev -- 上一层的dA 公式里面的dA^[l-1]
    dW -- 当前层的dW
    db -- 当前层的db
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = np.dot(dZ,A_prev.T) / m
    db = np.sum(dZ,axis=1,keepdims=True)/ m
    dA_prev = np.dot(W.T,dZ)

    return dA_prev, dW, db


def linear_activation_backward(dA, cache, activation):
    """
    实现 LINEAR->ACTIVATION 的反向传播
    
    Arguments:
    dA -- 当前层激活值的梯度l
    cache -- (linear_cache, activation_cache) 
    activation -- 激活函数: "sigmoid" 或 "relu"
    
    Returns:
    dA_prev -- 上一层激活值的梯度
    dW -- 当前层的dW
    db -- 当前层的db
    """
    linear_cache, activation_cache = cache
    
    #计算dL/dZ,当前层线性部分输出的梯度
    if activation == "relu":
        dZ = relu_backward(dA,activation_cache) 
        
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA,activation_cache)
        
    dA_prev, dW, db = linear_backward(dZ,linear_cache)

    return dA_prev, dW, db

下面要实现整个网络的反向传播了

反向传播从右到左，由输出计算梯度。我们知道这里的输出 $A^{[L]} = \sigma(Z^{[L]})$，首先需要计算损失值对 $A^{[L]}$的梯度：dAL $= \frac{\partial \mathcal{L}}{\partial A^{[L]}}$.

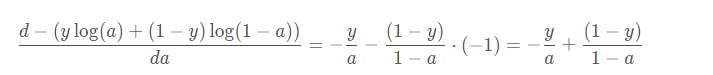
在神经网络基础中我们已经求出了dAL，下面转换成代码：

dAL = - np.divide(Y, AL) + np.divide(1 - Y, 1 - AL)

def L_model_backward(AL, Y, caches):
    """
    实现整个网络的反向传播 [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID
    
    Arguments:
    AL -- 网络的输出
    Y -- 标签向量 (0:非猫,1:猫), shape (1, 样本数)
    caches -- 缓存列表:    caches = [(linear_cache, activation_cache)]
              由于输入层(第0层)没有参数，因此caches[0]保存的是第1层的值
    
    Returns:
    grads -- 每层每个参数的梯度
             grads["dA" + str(l)] = ... 
             grads["dW" + str(l)] = ...
             grads["db" + str(l)] = ... 
    """
    # 反向传播 先计算L层激活值的梯度 dAL
    dAL = - np.divide(Y, AL) + np.divide(1 - Y, 1 - AL) 
    L = len(caches) #层数
    grads = {}
    
    # 计算L层的梯度
    current_cache = cache[L-1]#L层的缓存
    grads['dA' + str(L-1)],grads['dW' + str(L)],grads['db' + str(L)] = linear_activation_backward(dAL,current_cache,'sigmoid') #最后一层是sigmoid

    
    # 从L-2到0
    for l in reversed(range(L-1)):
        current_cache = cache[l]
        #计算l+1层的dW和dB 以及 l层(前一层)的dA
        grads['dA' + str(l)],grads['dW' + str(l+1)],grads['db' + str(l+1)] = linear_activation_backward(grads['dA' + str(l+1)],current_cache,'relu') 
    
    return grads
    

更新参数

我们用下面的公式更新参数：

$W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]} \tag{11}$
$b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} \tag{12}$

def update_parameters(parameters, grads, learning_rate):
    """
    更新参数
    
    Arguments:
    parameters -- 包含当前参数值的字典
    grads -- 包含梯度的字典
    
    Returns:
    parameters -- 包含更新后参数的字典
                  parameters["W" + str(l)] = ... 
                  parameters["b" + str(l)] = ...
    """
    
    L = len(parameters) // 2 # 层数

    # l从0到L-1
    for l in range(L):
        # 更新l+1层的参数
        parameters["W" + str(l+1)] -= learning_rate * grads['dW'+str(l+1)]
        parameters["b" + str(l+1)] -= learning_rate * grads['db'+str(l+1)]
    return parameters

至此整个神经网络的梯度下降算法实现完毕了，下面可以学习看看了。

数据集

import numpy as np
import h5py
    
    
def load_dataset():
    train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    classes = np.array(test_dataset["list_classes"][:]) # the list of classes
    
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
    
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

上面是加载数据集的代码，数据集下载

train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
# Example of a picture
index = 2
plt.imshow(train_set_x_orig[index])
print(train_set_x_orig.shape)

print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") +  "' picture.")
print(train_set_y.shape) #(1, 209)

我们看下数据集的样子，从输出可以看到，有209个 $64\times 64 \times3$像素(rgb)的图片。

处理数据集

可以看到数据集是一个多维数组，我们先把它们扁平化转换成(特征数,样本数)这样维度的数组。

train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T# train_set_x_orig.shape[0]就是样本数,-1代表让python自己算，最后进行转置，就得到了我们想要的结果
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T

print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))

输出为：

train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)

通常对于图像数据需要进行归一化处理，这里只要除以最大灰度值255即可。

train_x = train_set_x_flatten/255.
test_x = test_set_x_flatten/255.
test_y = test_set_y
train_y = train_set_y

这样我们把数据处理成我们想要的了。

使用深层网络

下面我们就用上面实现的深层网络来实现图像识别，我们网络结构是这样的：

接下来用上面的函数来实现我们深层网络模型：

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):#lr was 0.009
    """
    实现L层的神经网络: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
    
    Arguments:
    X -- 输入数据集X (num_px * num_px * 3, 样本数)
    Y -- 标签向量 (0:非猫,1:猫), shape (1, 样本数)
    layers_dims --  每层维度列表，比如[4,2,1]表示输入层4个特征，隐藏层2个神经元，最后是一个单元的输出层
    learning_rate -- 学习率
    num_iterations -- 迭代次数
    print_cost -- 是否打印损失值
    
    Returns:
    parameters -- 训练得到的参数值，可用于预测
    """
    np.random.seed(1)
    
    costs = []#保存历史cost
    
    
    # 初始化参数
    parameters = initialize_parameters_deep(layers_dims)
    
    for i in range(num_iterations):
        # 前向传播
        AL,caches = L_model_forward(X,parameters) #  最后一层激活值,[(  (A_prev, W, b)  ,   Z)] (L-1个)
        # 计算损失值
        cost = compute_cost(AL,Y)
        # 反向传播
        grads = L_model_backward(AL,Y,caches)
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)
        
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost) #添加到costs列表
    
    # plot the cost
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters

好了，终于可以训练我们的模型了，是不是期望能得到一个准确率高于70%的模型？

layers_dims = [12288, 20, 7, 5, 1] #  4-layer model

parameters = L_layer_model(train_x, train_y, layers_dims,num_iterations = 2500, print_cost = True)

输出

Cost after iteration 0: 0.693149
Cost after iteration 100: 0.678010
Cost after iteration 200: 0.667599
Cost after iteration 300: 0.660421
Cost after iteration 400: 0.655457
Cost after iteration 500: 0.652013
Cost after iteration 600: 0.649615
Cost after iteration 700: 0.647941
Cost after iteration 800: 0.646769
Cost after iteration 900: 0.645947
Cost after iteration 1000: 0.645368
Cost after iteration 1100: 0.644960
Cost after iteration 1200: 0.644673
Cost after iteration 1300: 0.644469
Cost after iteration 1400: 0.644325
Cost after iteration 1500: 0.644223
Cost after iteration 1600: 0.644151
Cost after iteration 1700: 0.644100
Cost after iteration 1800: 0.644063
Cost after iteration 1900: 0.644037
Cost after iteration 2000: 0.644019
Cost after iteration 2100: 0.644006
Cost after iteration 2200: 0.643997
Cost after iteration 2300: 0.643990
Cost after iteration 2400: 0.643985

从上面的输出我们可以隐隐察觉到哪里不对？

先实现准确率函数看下该模型的准确率是多少

def predict(X, y, parameters):

    m = X.shape[1] #样本数
    n = len(parameters) // 2 # 层数
    p = np.zeros((1,m))
    
    # 前向传播
    probas, caches = L_model_forward(X, parameters)

    
    # convert probas to 0/1 predictions
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0
    
    print("Accuracy: "  + str(np.sum((p == y)/m)))
        
    return p

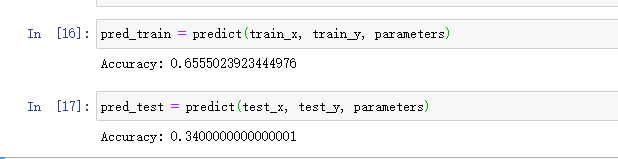
赶紧调用一下，结果大吃一惊，比我们逻辑回归的效果还差。

问题出现在了权值初始化上面，因为我们每层的权值初始化的分布都是一样的，*0.01后虽然不会发生梯度消失的问题，但是激活值的分布一样，导致多个神经元的输出几乎相同，激活值在分布上有所偏向，会出现表现力受限的问题。

那么怎么办呢，使用Xavier初始值。这些内容会在下篇文章中讲到，这里为了看到深层神经网络的效果，不得不提前使用下。

# 深层网络的参数初始化
def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- 每层维度列表，比如[4,2,1]表示输入层4个特征，隐藏层2个神经元，最后是一个单元的输出层
    
    Returns:
    parameters -- 返回包含参数 "W1", "b1", ..., "WL", "bL"的字典：
                    Wl --权重矩阵 (layer_dims[l], layer_dims[l-1])
                    bl --偏置向量 (layer_dims[l], 1)
    """
    
    np.random.seed(1)
    parameters = {}
    L = len(layer_dims)            # 网络的层数
    # 第0层表示输入层
    # 这里从1开始，到$L-1$
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1]) 
        parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
        
    return parameters

parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1])重点是这段代码，使用Xavier 初始值后，前一层的单元数越多，当前层的初始值的权重就越小。

我们再来训练一下。

layers_dims = [12288, 20, 7, 5, 1] #  4-layer model

parameters = L_layer_model(train_x, train_y, layers_dims,num_iterations = 2500, print_cost = True)

Cost after iteration 0: 0.771749
Cost after iteration 100: 0.672053
Cost after iteration 200: 0.648263
Cost after iteration 300: 0.611507
Cost after iteration 400: 0.567047
Cost after iteration 500: 0.540138
Cost after iteration 600: 0.527930
Cost after iteration 700: 0.465477
Cost after iteration 800: 0.369126
Cost after iteration 900: 0.391747
Cost after iteration 1000: 0.315187
Cost after iteration 1100: 0.272700
Cost after iteration 1200: 0.237419
Cost after iteration 1300: 0.199601
Cost after iteration 1400: 0.189263
Cost after iteration 1500: 0.161189
Cost after iteration 1600: 0.148214
Cost after iteration 1700: 0.137775
Cost after iteration 1800: 0.129740
Cost after iteration 1900: 0.121225
Cost after iteration 2000: 0.113821
Cost after iteration 2100: 0.107839
Cost after iteration 2200: 0.102855
Cost after iteration 2300: 0.100897
Cost after iteration 2400: 0.092878

这次看起来正常多了，再看下准确率。

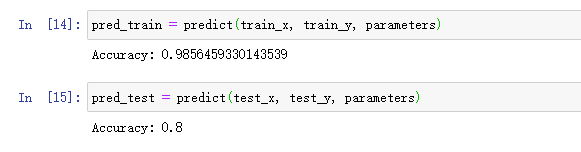
很好，准确率提高到了80%了，