tarjan对有向图的缩点(求强联通分量)
0x00 tarjan算法简介
tarjan算法是基于DFS的算法,核心在于巧妙的使用访问节点的时间戳 和 栈。
tarjan算法可以用于求解:
- 最近公共祖先(LCA);
- 有向图的强连通分量;
- 无向图的双连通分量;
- 割点;
- 桥;
本篇只介绍用tarjan算法来求解有向图的强连通分量。
强连通分量:当中任意两个节点互相可达(如果只有一个节点,这一个节点也是强连通分量)
基本思想:
定义两个数组low[],dfn[],
dfn[i]:记录访问节点i时的次序(时间戳);
low[i]:节点i可以追溯到的最小的时间戳;
dfs访问节点,
访问节点i时初始化: low[i] = dfn[i] = 访问编号,同时让节点i入栈,并标记i已经入栈。
在访问节点过程中,会不断更新low[]数组,当在回溯过程中发现low[i]==dfn[i]时,
说明此时形成了一个强连通分量,进行出栈操作(可进行染色标记这些节点属于强连通),
出栈元素等于此时的根节点后,停止出栈(元素出栈时,要记得标记已经出栈)。继续dfs。
下面来大概模拟一下下方这张图:
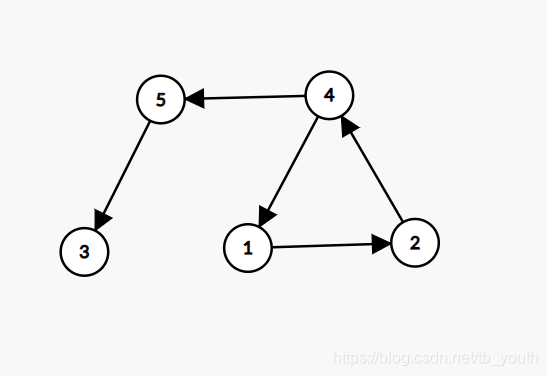
假设从1号节点开始dfs访问节点:
low[1] = dfn[1] = 1
stack = {1}
low[2] = dfn[2] = 2
stack = {1,2}
low[4] = dfn[4] = 3
stack = {1,2,4}
此时在4号节点,这里假设之后访问1号节点,
(当然之后也可能先访问5,最后结果是一样的)
发现1号节点已经在访问过(在栈中),
那么此时的4号节点的就可以更新,追溯最小的编号:
low[4] = min(low[4],dfn[1]) = 1。
继续dfs:
low[5]=dfn[5] = 4
stack = {1,2,4,5}
low[3] = dfn[3] = 5
stack = {1,2,4,5,3}
根节点在3,没有节点可以访问了,递归返回:
发现:low[3] = dfn[3]:
stack中元素出栈(染色进行标记),出栈元素等于此时的根节点后,停止出栈。
此时出栈的只有:3
{3}是一个强连通分量;
stack = {1,2,4,5}
继续 递归返回到 5:
low[5] = min(low[5],low[3]) = min(4,5) = 4
出现了:low[5] = dfn[5]
stack中元素出栈(染色进行标记),出栈元素等于此时的根节点后,停止出栈。
此时出栈的只有:5
{5}也是一个强连通分量;
stack = {1,2,4}
继续 递归返回到 4:
low[4] = min(low[4],low[5]) = min(1,4) = 1
low[4] != dfn[4]
继续 递归返回到 2:
low[2] = min(low[2],low[4]) = min(2,1) = 1
low[2] != dfn[2]
继续 递归返回到 1:
low[1] = min(low[1],low[2]) = min(1,1) = 1
出现了:low[1] == dfn[1]
stack中元素出栈(染色进行标记),出栈元素等于此时的根节点后,停止出栈。
{4,2,1}是一个强连通分量。
stack = {}
最终的强连通分量分别为:{3},{5},{4,2,1}
(…具体看下面代码,自己手动模拟一遍就能够懂,不好画图,文字表述实在辛苦。。)
0x01题目
洛谷p2863
有一个 n个点,m 条边的有向图,请求出这个图点数大于 1 的强联通分量个数。
0x02代码
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 5e4+5;
const int P = 1e4+5;
int n,m;
struct Edge
{
int from;
int to;
int next;
}edge[N];
int head[N],id;
int low[P];
int dfn[P];
int st[P];
bool vis[P];
int top;
int color[P];
int dfn_num;
int color_num;
int ans;
inline void add_edge(int from,int to)
{
edge[id].from = from;
edge[id].to = to;
edge[id].next = head[from];
head[from] = id++;
}
void init()
{
memset(head,-1,sizeof(head));
id = 0;
}
void tarjan(int u)
{
st[++top] = u;
vis[u] = true;
dfn[u] = ++dfn_num;
low[u] = dfn_num;
for(int i = head[u]; ~i; i = edge[i].next)
{
int to = edge[i].to;
if(!dfn[to])
{
tarjan(to);
low[u] = min(low[u],low[to]);
}
else if(vis[to])
low[u] = min(low[u],dfn[to]);
}
if(dfn[u] == low[u])
{
color[u] = ++color_num;
int cnt = 1;
vis[u] = false;
while(st[top] != u)
{
color[st[top]] = color_num;
cnt++;
vis[st[top--]] = false;
}
ans += cnt > 1;
top--;
}
}
int main()
{
cin>>n>>m;
init();
while(m--)
{
int a,b;
cin>>a>>b;
add_edge(a,b);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
cout<<ans<<endl;
return 0;
}