二二、方程Ax=b的行空间中的解

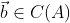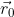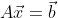1. 假设  , 那么，行空间中存在唯一的元素 ，是  的解

一个解对应一个n0，但所有解对应一个r0

证明，假设：

那么：

Rn中存在一个或多个向量x，满足上面的等式

下面画出Rn，矩阵A的列空间、零空间，A的零空间的正交补：

其中：

根据前面的介绍，假设：

那么

唯一性证明：

假设行空间中的r1也满足上面的方程，则：

又因为行空间是子空间，因此：

因此：

既属于A的行空间，又属于A的零空间，所以

因此，如果向量b属于列空间，那么行空间中存在唯一的向量，满足Ax=b等式