机器学习笔记-朴素贝叶斯

朴素贝叶斯算法

朴素贝叶斯(Naive Bayes)是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对于给定的输入\(x\)，利用贝叶斯定理求出后验概率最大的输出\(y\)。

1. 概率论基础

条件概率

条件概率是指事件\(A\)在另外一个事件\(B\)已经发生条件下的发生概率。此时，条件概率表示为：\(P(A|B)\)，读作“在\(B\)条件下\(A\)的概率”。若只有两个事件\(A\)，\(B\)，如图，那么：

\[P(A|B) = \cfrac{P(AB)}{P(B)} \tag{1.1} \]

同理，在\(A\)条件下\(B\)的概率

\[P(B|A) = \cfrac{P(AB)}{P(A)} \tag{1.2} \]

若\(P(A) = P(A|B)\)，则\(B\)的发生与否对\(A\)发生的可能性毫无影响。这是在概率论上就称\(A,B\)两事件独立，而由式\((1.1)\)得出

\[P(AB) = P(A)\cdot P(B) \tag{1.3} \]

若两事件\(A,B\)满足式\((1.3)\)，则称\(A,B\)独立。

根据式\((1.1)\)和\((1.2)\)有

\[P(AB) = P(A|B)\cdot P(B) = P(B|A)\cdot P(A) \tag{1.4} \]

进一步，得到了贝叶斯定理，即

\[P(A|B) = \cfrac{P(B|A)\cdot P(A)}{P(B)} \tag{1.5} \]

全概率公式：表示若事件\(A_1,A_2,\cdots,A_n\)构成一个完备事件组且都有正概率，则对任意一个事件\(B\)都有公式成立。

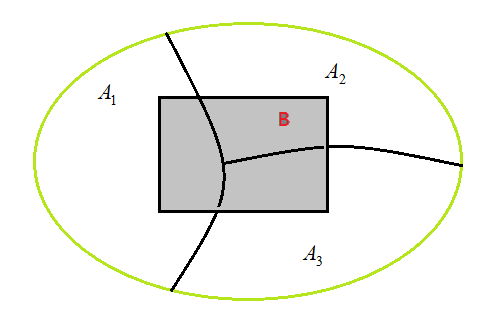
全概率公式

\[\begin{aligned} P(B) &= P(A_1B + A_2B + \cdots + A_nB) \\ &= P(A_1B) + P(A_2B) + \cdots + P(A_nB) \\ & = \sum_{i=1}^n P(A_iB) \end{aligned} \tag{1.6}\]

根据条件概率公式，

\[P(B) = \sum_{i=1}^n P(B|A_i)\cdot P(A_i) \tag{1.7} \]

贝叶斯公式是将全概率公式式\((1.7)\)带入到贝叶斯定理式\((1.5)\)中，对于事件\(A_k\)和事件\(B\)有：

\[P(A_k|B) = \cfrac{P(B|A_k)\cdot P(A_k)}{\sum_{i=1}^n P(B|A_i)\cdot P(A_i)} \tag{1.8} \]

其中，\(P(A_k)\)为先验概率(prior probability)，\(P(A_k|B)\)为后验概率(posterior probability)，\(P(B|A_k)\)为似然函数(likelihood function)，\(\sum_{i=1}^n P(B|A_i)\cdot P(A_i)\)为归一化项，对于\(P(A_k|B)\)来说为固定值，如果我们只需要比较后验概率\(P(A_k|B)\)的大小，可以将其忽略，并不会影响结果。

2. 特征条件独立假设

注意，样本\(x\)有\(n\)个特征\(x=(x_1,x_2,\cdots,x_n)\)，此时\(P(y_k|x) = P(x_1,x_2,\cdots,x_n|y_k)\cdot P(y_k)\)，条件概率分布\(P(x|y_k)\)有指数级数量的参数，其估计实际上是不可行的。

朴素贝叶斯法对条件概率分布作了特征条件独立性假设。

最终公式为：\(P(y_k|x)= \prod P(x_i|y_k)\cdot P(y_k)\)。

举个例子，如果应用在自然语言处理中，就是说在文章类别确定的条件下，文章的各个特征(单词)是独立的，并不相关。用通俗的话说，在文章类别确定的条件下，文章各个词之间出现与否没有相关性(事实上，并不成立)。所以这是一个非常强的假设，朴素贝叶斯法也因此得名（可能因为这个假设有点naive），但对问题的求解来说变得更加简单，但有时会牺牲一定的分类准确率。

3. 朴素贝叶斯算的基本方法

设输入空间\(\mathcal{X} \subseteq R^n\)为\(n\)维向量的集合，输出空间为类标记集合\(\mathcal{Y}=\{c_1,c_2,\cdots,c_K\}\)。输入为特征向量\(x \in \mathcal{X}\)，输出为类标记\(y \in \mathcal{Y}\)。\(X\)是定义在输入空间上的随机向量，\(Y\)是定义在输出空间上的随机变量。\(P(X,Y)\)是\(X\)和\(Y\)的联合概率分布。训练数据集

\[T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\} \]

由\(P(X,Y)\)独立同分布产生。

朴素贝叶斯法通过训练数据集学习联合概率分布\(P(X,Y)\)。具体地，学习以下先验概率分布和条件概率分布。

先验概率分布

\[P(Y=c_k), \quad k=1,2,\cdots,K \tag{3.1} \]

条件概率分布

\[P(X=x|Y=c_k) = P(X^{(1)}=x^{(1)},X^{(2)}=x^{(2)},\cdots,X^{(n)}=x^{(n)}|Y=c_k), \quad k=1,2,\cdots,K \tag{3.2} \]

于是学习到联合概率分布\(P(X,Y)\)。

根据条件独立性假设，式\((3.2)\)等价于

\[P(X=x|Y=c_k) = \prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k) \tag{3.3} \]

朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成模型。

在分类时，对给定的输入\(x\)，通过学习到的模型计算后验概率分布\(P(Y=c_k|X=x)\)，将后验概率最大的类作为\(x\)的类输出。后验概率计算根据贝叶斯公式进行：

\[P(Y=c_k|X=x)=\cfrac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_kP(X=x|Y=c_k)P(Y=c_k)} \tag{3.4} \]

将式\((3.3)\)代入\((3.4)\)，有

\[P(Y=c_k|X=x)=\cfrac {P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)} , \quad k=1,2,\cdots,K \tag{3.5} \]

这是朴素贝叶斯法的基本公式。于是，朴素贝叶斯分类器可表示为

\[y=f(x)=\text{arg}\smash{\max_{c_k}}\cfrac {P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_k P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)} , \quad k=1,2,\cdots,K \tag{3.6} \]

式\((3.6)\)中的分母对所有\(c_k\)都是相同的，所以，

\[y=\text{arg}\smash{\max_{c_k}}{P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)} \tag{3.7} \]

4. 朴素贝叶斯的参数估计

我们只要求出\(P(Y=c_k)\)和\(P(X^{(j)}=x^{(j)}|Y=c_k), j=1,2,\cdots,n\)，通过比较就可以得到朴素贝叶斯对输入向量\(x\)的推断结果。

那么，怎么通过训练集计算这两个概率呢？

对于\(P(Y=c_k)\)比较简单，通过极大似然估计，我们很容易得到\(P(Y=c_k)\)为样本类别\(c_k\)出现的频率，即样本类别\(c_k\)出现的次数\(m_k\)除以样本总数\(N\)，即

\[P(Y=c_k) = \cfrac{m_k}{N} \]

对于\(P(X^{(j)}=x^{(j)}|Y=c_k)\)，取决于我们的先验条件：

a）如果我们的\(X^{(j)}\)是离散值，那么，我们可以假设\(X^{(j)}\)服从多项式分布，这样得到\(P(X^{(j)}=x^{(j)}|Y=c_k)\)是在样本类别\(c_k\)中，特征\(x^{(j)}\)出现的频率。即：

\[P(X^{(j)}=x^{(j)}|Y=c_k) = \cfrac{m_{kj}^{(j)}}{m_k} \]

其中，\(m_k\)为样本类别\(c_k\)总的特征计数，而\(m_{kj}^{(j)}\)表示类别为\(c_k\)的样本中第\(j\)维特征\(x^{(j)}\)出现的计数。

b）如果我们的\(X^{(j)}\)是非常稀疏的离散值，即各个特征出现概率很低，这时我们可以假设\(X^{(j)}\)服从伯努利分布，即特征\(X^{(j)}\)出现记为\(1\)，不出现记为\(0\)。只要\(X^{(j)}\)出现即可，我们不关注\(X^{(j)}\)的次数。这样得到\(P(X^{(j)}=x^{(j)}|Y=c_k)\)是在样本类别\(c_k\)中，特征\(x^{(j)}\)出现的频率。即：

\[P(X^{(j)}=x^{(j)}|Y=c_k) = P(X^{(j)}=1|Y=c_k)x^{(j)} + (1 - P(X^{(j)}=1|Y=c_k))(1-x^{(j)}) \]

其中，\(x^{(j)}\)取值\(0\)和\(1\)。

c）如果我们的\(X^{(j)}\)是连续值，我们通常取\(X^{(j)}\)的先验概率为正态分布，即在样本类别\(c_k\)中，\(X^{(j)}\)的值服从正态分布。这样\(P(X^{(j)}=x^{(j)}|Y=c_k)\)的概率分布是：

\[P(X^{(j)}=x^{(j)}|Y=c_k) = \cfrac{1}{\sqrt{2\pi\sigma_k^2}}exp \bigg({-\frac{(x^{(j)}-\mu_k)^2}{2\sigma^2_k}}\bigg) \]

其中，\(\mu_k\)和\(\sigma^2_k\)是正态分布的期望和方差，可以通过极大似然估计求得。\(\mu_k\)为在样本类别\(c_k\)中所有\(X^{(j)}\)的平均值。\(\sigma^2_k\)为在样本类别\(c_k\)中所有\(X^{(j)}\)的方差。对于一个连续的样本值，带入正态分布的公式，就可以求出概率分布了。

5. 朴素贝叶斯算法过程

输入：训练数据\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\)，其中\(x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T\)，\(x_i^{(j)}\)是第\(i\)个样本的第\(j\)个特征，\(x_i^{(j)} \in \{a_{j1},a_{j1},\cdots,a_{jS_j}\}\)，\(a_{jl}\)是第\(j\)个特征可能取的第\(l\)个值，\(j=1,2,\cdots,n\)，\(l=1,2,\cdots,S_j\)，\(y_i \in \{c_1,c_2,\cdots,c_K\}\)；实例\(x\)；

输出：实例\(x\)的分类。

1）计算\(Y\)的\(K\)个先验概率：

\[P(Y=c_k) = \cfrac{\sum_{i=1}^NI(y_i=c_k)}{N}, \quad k=1,2,\cdots,K \]

2）分别计算类别\(c_k\)中样本的第\(j\)个特征的\(a_{jl}\)取值的条件概率：

a）如果是离散值：

\[P(X^{(j)}=a_{jl}|Y=c_k) = \cfrac{\sum_{i=1}^NI(x^{(j)}=a_{jl},y_i=c_k)}{\sum_{i=1}^NI(y_i=c_k)} \]

b）如果是稀疏二项离散值：

\[P(X^{(j)}=a_{jl}|Y=c_k) = P(a_{jl}|Y=c_k)a_{jl}+(P(a_{jl}|Y=c_k))(1-a_{jl}) \]

此时\(a_{jl}\)只有两种取值。

c）如果是连续值，不需要计算各\(a_{jl}\)取值的概率，直接求正态分布的参数：

\[P(X^{(j)}=x^{(j)}|Y=c_k) = \cfrac{1}{\sqrt{2\pi\sigma_k^2}}exp \bigg({-\frac{(x^{(j)}-\mu_k)^2}{2\sigma^2_k}}\bigg) \]

需要求出\(\mu_k\)和\(\sigma^2_k\)。\(\mu_k\)为在样本类别\(c_k\)中所有\(X^{(j)}\)的平均值。\(\sigma^2_k\)为在样本类别\(c_k\)中所有\(X^{(j)}\)的方差。

3）对于给定的实例\(x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T\)，计算

\[{P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)} \]

4）确定实例\(x\)的类

\[y=\text{arg}\smash{\max_{c_k}}{P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)} \]

从上面的计算可以看出，没有复杂的求导和矩阵运算，因此效率很高。

6. 贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0的情况。这时会影响到后验概率的计算结果，使分类产生偏差。解决这一问题的方法是采用贝叶斯估计。具体地，条件概率的贝叶斯估计是

\[P(X^{(j)}=a_{jl}|Y=c_k) = \cfrac{\sum_{i=1}^NI(x^{(j)}=a_{jl},y_i=c_k)+\lambda}{\sum_{i=1}^NI(y_i=c_k)+S_j \lambda} \tag{6.1} \]

式中\(\lambda \ge 0\)。等价于在随机变量各个取值的频数上赋予一个正数\(\lambda \gt 0\)。当\(\lambda = 0\)时就是极大似然估计。常取\(\lambda = 1\)，这时称为拉普拉斯平滑(Laplacian smoothing)。显然，对于任何\(l=1,2,\cdots,S_j\)，\(k=1,2,\cdots,K\)，有

\[P_\lambda(X^{(j)}=a_{jl}|Y=c_k) \gt 0 \]

\[\sum_{l=1}^{S_j}P(X^{(j)}=a_{jl}|Y=c_k) = 1 \]

表明式\((6.1)\)确为一种概率分布。同样，先验概率的贝叶斯估计是

\[P_\lambda(Y=c_k) = \cfrac{\sum_{i=1}^NI(y_i=c_k) + \lambda}{N + K\lambda} \tag{6.2} \]

7. 举个例子

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.460	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	0.774	0.376	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	0.634	0.264	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	0.608	0.318	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	0.556	0.215	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	0.403	0.237	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	0.481	0.149	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	0.437	0.211	是
9	乌黑	稍蜷	沉闷	硝糊	稍凹	硬滑	0.666	0.091	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	0.243	0.267	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	0.245	0.057	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	0.343	0.099	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	0.639	0.161	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬情	0.657	0.198	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	0.360	0.370	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	0.593	0.042	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	0.719	0.103	否

数据集为西瓜数据集3.0，机器学习-周志华，p84

我们使用该数据集训练一个朴素贝叶斯分类器，对如下测试例进行分类

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
测 1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.460	？

首先估计类先验概率\(P(Y=c_k)\)，显然有

\[P(好瓜=是) = \cfrac{8}{17} \approx 0.471 \]

\[P(好瓜=否) = \cfrac{9}{17} \approx 0.529 \]

然后，为每个特征估计条件概率\(P(X^{(j)}=x^{(j)}|Y=c_k)\)：

\[P_{青绿|是} = P(色泽=青绿|好瓜=是) = \cfrac{3}{8} = 0.375 \]

\[P_{青绿|否} = P(色泽=青绿|好瓜=否) = \cfrac{3}{9} \approx 0.333 \]

\[P_{蜷缩|是} = P(根蒂=蜷缩|好瓜=是) = \cfrac{5}{8} = 0.625 \]

\[P_{蜷缩|否} = P(根蒂=蜷缩|好瓜=否) = \cfrac{3}{9} \approx 0.333 \]

\[P_{浊响|是} = P(敲声=浊响|好瓜=是) = \cfrac{6}{8} = 0.750 \]

\[P_{浊响|否} = P(敲声=浊响|好瓜=否) = \cfrac{4}{9} \approx 0.444 \]

\[P_{清晰|是} = P(纹理=清晰|好瓜=是) = \cfrac{7}{8} = 0.875 \]

\[P_{清晰|否} = P(纹理=清晰|好瓜=否) = \cfrac{2}{9} \approx 0.222 \]

\[P_{凹陷|是} = P(脐部=凹陷|好瓜=是) = \cfrac{6}{8} = 0.750 \]

\[P_{凹陷|否} = P(脐部=凹陷|好瓜=否) = \cfrac{2}{9} \approx 0.222 \]

\[P_{硬滑|是} = P(触感=硬滑|好瓜=是) = \cfrac{6}{8} = 0.750 \]

\[P_{硬滑|否} = P(触感=硬滑|好瓜=否) = \cfrac{6}{9} \approx 0.667 \]

\[\begin{aligned} p_{密度:0.697|是} &= p(密度=0.697|好瓜=是) \\ &= \cfrac{1}{\sqrt{2\pi}\times 0.129}exp\bigg(-\cfrac{(0.697-0.574)^2}{2\times 0.129^2}\bigg) \approx 1.959 \end{aligned}\]

\[\begin{aligned} p_{密度:0.697|否} &= p(密度=0.697|好瓜=否) \\ &= \cfrac{1}{\sqrt{2\pi}\times 0.195}exp\bigg(-\cfrac{(0.697-0.496)^2}{2\times 0.195^2}\bigg) \approx 1.203 \end{aligned}\]

\[\begin{aligned} p_{含糖:0.460|是} &= p(含糖=0.460|好瓜=是) \\ &= \cfrac{1}{\sqrt{2\pi}\times 0.101}exp\bigg(-\cfrac{(0.697-0.279)^2}{2\times 0.101^2}\bigg) \approx 0.788 \end{aligned}\]

\[\begin{aligned} p_{含糖:0.460|否} &= p(含糖=0.460|好瓜=否) \\ &= \cfrac{1}{\sqrt{2\pi}\times 0.108}exp\bigg(-\cfrac{(0.697-0.154)^2}{2\times 0.108^2}\bigg) \approx 0.066 \end{aligned}\]

于是，有

\[P(好瓜=是) \times P_{青绿|是} \times P_{蜷缩|是} \times P_{浊响|是} \times P_{清晰|是} \times P_{凹陷|是} \times P_{硬滑|是} \times p_{密度:0.697|是} \times p_{含糖:0.460|是} \approx 0.038 \]

\[P(好瓜=否) \times P_{青绿|否} \times P_{蜷缩|否} \times P_{浊响|否} \times P_{清晰|否} \times P_{凹陷|否} \times P_{硬滑|否} \times p_{密度:0.697|否} \times p_{含糖:0.460|否} \approx 6.80 \times 10^{-5} \]

由于\(0.038 \gt 6.80 \times 10^{-5}\)，因此，朴素贝叶斯分类器将测试样本“测 1”判别为“好瓜”。

注意：实践中常通过取对数的方式来将"连乘"转化为"连加"以避免数值下溢。

若某个特征值在训练集中没有与某个类同时出现过，则直接进行条件概率估计将出现问题。例如，在使用上述西瓜数据集训练朴素贝叶斯分类器时，对一个"敲声=清脆"的测试例，有

\[P_{清脆|是} = P(敲声=清脆|好瓜=是) = \cfrac{0}{8} = 0 \]

由于连乘式计算出的概率值为零，因此，无论该样本的其他属性是什么，哪怕在其他属性上明显像好瓜，分类的结果都将是“好瓜=否”，这显然太合理。此时就要用到上一节提到的贝叶斯估计，常用的是拉普拉斯平滑。

8. 朴素贝叶斯算法小结

朴素贝叶斯的主要优点有：

朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
对缺失数据不太敏感，算法也比较简单，常用于文本分类。

朴素贝叶斯的主要缺点有：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
对输入数据的表达形式很敏感。

参考来源：

1）统计学习方法 - 李航

2）机器学习 - 周志华

3）朴素贝叶斯算法原理小结-刘建平Pinard

4）朴素贝叶斯算法的理解与实现

5）机器学习之朴素贝叶斯算法详解