动态规划是一种优化多阶段决策问题的策略,现实中有一类问题的解决过程可以按时间先后或规模从小到大分成多个的阶段,在它的每一阶段都需要作出决策,决策的造成结果就是状态,上一阶段的状态会影响下一阶段的决策,所以每个阶段的状态可以直接由上一阶段的状态通过一定的规律推出,根据这个规律可以建立状态转移方程,把前面阶段的状态记录下来,通过状态转移方程就可以推出最后阶段的状态,最后阶段的状态就是整个问题最优值,整个过程的所有阶段的状态对应的一个决策序列就是最优解。
动态规划的适用范围:
(1)最优子结构。如果一个问题的最优解中包含了其子问题的最优解,就说该问题具有最优子结构。当一个问题具有最优子结构时,我们就可以考虑使用动态规划法去实现它。
(2)重叠子问题。重叠子问题是指用来解原问题的递归算法会反复求解同样子问题,当一个递归算法不断地调用同一个问题时,就说明该问题包含了重叠子问题。此时如果用分治法求解,会反复求解同样的问题,效率低下。
动态没有统一的处理方法,必须根据问题的各种性质并结合一定的技巧来处理。
【例1】设 A[1..N]是 N 个正整数的有序序列,x 是一个正整数。需要设计一个算法来确定在 A 中是否有两个元素之和恰好为 x。
初始时和为x的两个加数范围是A[1]—A[N],设s= A[1]+A[N],因为A是正整数升序,左加数A[1]的下标往前移动一位会增大s,右加数A[N]的下标往后移动一位会减小s,所以s>x时s= A[1]+A[N-1],s<x时s= A[1+1]+A[N],直到s=x,就找到答案了。

1 /**在正整数升序数组a中寻找两个和为x的元素并打印结果
2 * @param a
3 * @param x
4 * T(n)=O(n),S(n)=O(1)
5 */
6 private static void sum(int[]a,int x){
7 int min = 0;
8 int max = a.length - 1;
9 while(min < max) {
10 int s = a[min] + a[max];
11 //如果和大于x说明当前最大数加上arr[min]之后的小数都比x大
12 if (s > x) {
13 max--;
14 //如果和小于x说明当前最小数加上arr[max]之前的数都比x小
15 } else if (s < x) {
16 min++;
17 } else if (s == x){
18 System.out.println("["+a[min]+","+a[max]+"]");
19 break;
20 }
21 }
22 if (min == max) {
23 System.out.println("数组中没有两个元素和等于x");
24 }
25 }
26 /*复杂度分析:长度为n的数组每个元素只扫描了一次,最多循环n次,所以T(n)=O(n),方法只声明了两个变量,S(n)=O(1)*/
【例2】输入一个整形数组(可能有正数、0、或负数),求数组的一个连续的且所有元素和最小的子数组。
设第一个元素为当前最优值,再设子集元素和为0,从数组的第一个元素开始遍历,每次循环中先判断之前的子集元素和是否<0,是则直接累加当前元素,否则先清零再累加,然后判断子集元素和是否<最优值,是则更新最优值。

1 /**寻找一个整数数组的一个所有元素和最小的连续子集
2 * @param a
3 * T(n)=O(n),S(n)=O(1)
4 */
5 public static void findMinSubarray(int[] a){
6 //最优值
7 int minSum = a[0];
8 //最优解的首尾下标
9 int minF = 0,minL = 0;
10 //当前记录的子集的所有元素和
11 int currSum = 0;
12 //当前记录的子集的首尾下标
13 int currF=0,currL;
14 for (int i = 0; i < a.length; i++) {
15 if (currSum>0){
16 currSum=0;
17 currF=i;
18 }
19 currSum += a[i];
20 currL=i;
21 if (currSum < minSum) {
22 minSum = currSum;
23 minF=currF;
24 minL=currL;
25 }
26 }
27 System.out.println("最优值为:"+minSum);
28 System.out.print("最优解为:[");
29 for (int i = minF; i < minL; i++) {
30 System.out.print(a[i]+",");
31 }
32 System.out.println(a[minL]+"]");
33 }
34 /*数组长度为n时,循环n次,T(n)=O(n)。只申请了几个变量,没有调用其他方法,S(n)=O(1)*/
【例3】完全加括号的矩阵连乘积:给定 k 个矩阵{M1, M2, ..., Mk},其中 Mi 与 Mi+1 是可乘的,i = 1, 2, …, n - 1。考察这 n 个矩阵的连乘积 M1M2...Mk:
矩阵A与矩阵B可乘的条件为矩阵A的列数等于矩阵B的行数,若A是一个p*q的矩阵,B是一个q*r的矩阵,则其乘积C=AB是一个p*r的矩阵。由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
例如:
计算三个矩阵连乘{A1,A2,A3};维数分别为10*100 , 100*5 , 5*50
按此顺序计算需要的次数((A1*A2)*A3):10X100X5+10X5X50=7500次
按此顺序计算需要的次数(A1*(A2*A3)):100X5X50+10X100X50=75000次
如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的计算次数最少?
实例:

首先按规模从小到大分阶段,最小的阶段是俩个矩阵连乘,最大的是六个矩阵连乘,设一个二维数组存放每个连乘矩阵(阶段)的最小相乘次数(状态):m[i][j]表示连乘矩阵Mi*Mi+1*Mi+2…Mj-1*Mj的状态。设一个一维数组存放所有矩阵的行数和列数:mrc[n+2]={0,18,35,25,17,10,21,36}。

先对规模小的阶段做决策并记录其状态,再根据规模小的阶段的状态推出规模大的阶段的状态。两个矩阵连乘的状态可以直接算出,三个矩阵连乘的状态就要选一个位置加括号,也就是做决策,做了决策就分成两个前面计算过的部分,可以直接算出。例如m[1][3],设加括号的位置为k,则根据矩阵乘法公式有:m[1][3]= m[1][k]+m[k+1][3]+p[1]*p[k+1]*p[3+1],遍历k的每个值,就能算出连乘矩阵M1*M2*M3的最小相乘次数。其实这个计算方法对两个矩阵连乘时也适用,所以可以合并。由上述分析推出该问题的状态转移方程:
i=j 时:m[i][j]= 0; i<j 时:m[i][j]= min{m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1]}(i<=k<j);

1 /** 计算矩阵的最小相乘次数
2 * @param mrc 矩阵数据
3 * T(n)=O(n^3),S(n)=O(n^2)
4 */
5 private static void matrix(int[] mrc){
6 //矩阵个数
7 int n = mrc.length-2;
8 //记录每个阶段的状态值
9 int[][] m = new int[n+1][n+1];
10 for (int r = 1; r < n; r++) {
11 for (int i = 1; i <= n-r; i++) {
12 //因为规模必须严格地从小到大,所以要设置变量使for循环沿对角线方向遍历数组
13 int j = i+r;
14 //先设个最大值,然后遍历k寻找最小值
15 m[i][j] = Integer.MAX_VALUE;
16 for (int k = i; k < j; k++) {
17 m[i][j] = Math.min(m[i][j],m[i][k]+m[k+1][j]+mrc[i]*mrc[k+1]*mrc[j+1]);
18 }
19 }
20 }
21 System.out.println(m[1][n]);
22 }/*3层循环,与n正相关,T(n)=O(n^3),辅助数组长度n^2,S(n)=O(n^2)*/
【例4】给定两个序列 Xm = {x1, x2, …, xm}和 Yn = {y1, y2, …, yn},利用动态规划算法求解 Xm和 Yn 的最长公共子序列。
当xm=yn时,Xm和Yn的LCS=Xm-1和Yn-1的LCS在尾部加上xm(yn)。当xm≠yn时,Xm和Yn的LCS=Xm-1和Yn的LCS与Xm和Yn-1的LCS中的较长者。LCS具有最优子结构性质且子问题重复。先用动态规划算出LCS的长度,即最优值,并记录获得最优值的子序列,再根据最优值和对应的子序列递归地构造最优解。
设一数组c[m][n]记录子问题的最优值,c[i][j]表示Xi和Yj的LCS长度,空序列的LCS也是空序列,所以c[0][0]=0。根据上面的分析可以得出最优值的动态规划函数:


1 import java.util.ArrayList;
2 /**
3 * @author 矜君
4 * @date 2020/6/6 11:07.
5 */
6 public class LCS {
7 public static void main(String[] args) {
8 //设一个空值防止数组下标越界
9 char[] x = {' ','w','e','c','h','a','t'};
10 char[] y = {' ','h','u','a','w','e','i'};
11 int m = x.length;
12 int n = y.length;
13 //记录最长公共子序列
14 ArrayList<Character> lcs = new ArrayList<>();
15 //记录获得最优值的子序列,辅助构造LCS
16 int[][] b = new int[m][n];
17 lcsLength(x,y,m,n,b);
18 findLCS(lcs,b,x,m-1,n-1);
19 System.out.println(lcs);
20 }
21 /**动态规划求两字符数组的最长公共子序列的长度
22 * @param x
23 * @param y
24 * @param m x的长度
25 * @param n y的长度
26 * @param b 记录每个阶段获得最优值的子序列,长度b[m][n]
27 * T(n)=O(mn),S(n)=O(mn)
28 */
29 private static void lcsLength(char[] x,char[] y,int m,int n,int[][]b){
30 //记录子序列的最优值
31 int[][] len = new int[m][n];
32 //遍历两个序列
33 for (int i = 1; i < m; i++) {
34 for (int j = 1; j < n; j++) {
35 //如果两(子)序列的尾元素相等,就可以确定一个属于LCS的元素
36 if (x[i]==y[j]){
37 len[i][j] = len[i-1][j-1] + 1;
38 b[i][j] = 1;
39 /*如果两(子)序列的尾元素相等,则其中至少有一个尾元素肯定不属于LCS,
40 根据前面已经记录的更小的子序列的LCS长度可以判断哪个尾元素不属于LCS*/
41 }else if (len[i-1][j]>=len[i][j-1]){
42 len[i][j] = len[i-1][j];
43 b[i][j] = 2;
44 }else {
45 len[i][j] = len[i][j-1];
46 b[i][j] = 3;
47 }
48 }
49 }
50 //打印LCS的长度
51 System.out.println(len[m-1][n-1]);
52 }/*双层循环(m-1)(n-1)次,T(n)=O(mn)。需要辅助空间len+b=2mn,S(n)=O(mn)*/
53
54 /** 根据最优值的情况排除不属于LCS的元素,递归地构造最长公共子序列
55 * @param lcs 记录最长公共子序列
56 * @param b 记录最优值对应的子序列
57 * @param x 其中一个字符数组
58 * @param i b[i][j],初始时i=m,j=n,从最后的元素开始往前搜索
59 * @param j
60 * T(n)=O(m+n),S(n)=O(mn)
61 */
62 private static void findLCS(ArrayList<Character> lcs, int[][] b, char[]x, int i , int j){
63 if (i==0 || j==0){
64 return;
65 }
66 //b[i][j] == 1说明x[i]=y[j],把x[i]放入LCS
67 if (b[i][j] == 1){
68 findLCS(lcs,b,x,i-1,j-1);
69 lcs.add(x[i]);
70 //b[i][j] == 2说明当前x的(子)序列的尾元素x[i]不属于LCS,删掉继续递归
71 }else if (b[i][j] == 2){
72 findLCS(lcs,b,x,i-1,j);
73 }else {//b[i][j] == 3说明当前y的(子)序列的尾元素y[j]不属于LCS,删掉继续递归
74 findLCS(lcs,b,x,i,j-1);
75 }
76 }/*因为i=m,j=n,每次递归-1,最多递归m+n次T(n)=O(m+n)。需要辅助空间b长度mn,lcs长度最多n或m,S(n)=O(mn)。*/
77 }
【例5】装载问题:有一批共 n 个集装箱要装上 2 艘载重量分别为 c1 和 c2 的轮船,其中集装箱 i 的重量为 wi,且所有集装箱的总重量不大于两艘船的总容量,装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这 2 艘轮船。如果有,找出一种装载方案。实例:集装箱重量:{3,4,4,5,7},c1=10,,c2=15
这个问题只需要考虑第一艘船的最优装载,只要尽可能把一船装满,剩下的装二船就可以了。
集装箱装船是一个多阶段决策问题,每个阶段的决策就是一个集装箱装与不装一船这两个选择,决策造成的状态就是一船的当前装载量,当前阶段的决策要依赖上一阶段的状态。除此之外此问题的决策还要考虑其他的条件限制,当前集装箱能不能装船还要考虑一船的剩余容量。为了方便后面阶段的决策,在当前阶段要对1船剩余容量的每个情况分别做出决策获得多个状态并存储到数组,下一阶段做决策时可以先把当前的集装箱装船,剩余的容量无论是多少都可以从数组中调用前面阶段的装载情况。
先设一个一维数组存储每个集装箱的重量:int[] w = {0,3,4,4,5,7}; 忽略开头的元素w[0],w[i]对应编号为i的集装箱的重量。然后设一个二维数组记录每个阶段的所有状态:int[][] cw = new int[n+1][c1+1]; 如图把二维数组cw以表格形式表示,i和j是数组下标,i表示集装箱编号,j表示一船剩余容量,一维数组w放在左边方便参考对应编号的集装箱重量。cw[i][j]表示在背包剩余容量为j时对集装箱i做出的决策造成的状态。
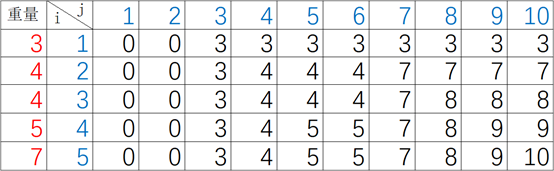
cw[2][4]表示剩余容量为j=4时第2个集装箱的决策造成的状态,2号集装箱的重量w[2]=4,首先判断2号集装箱能不能装下,如果不能装下的话当前状态cw[2][4]就等于上一阶段j=4时的状态cw[2-1][4],能装下再判断装不装,不装的话当前状态还是等于cw[2-1][4],装的话留给之前阶段的剩余容量为j-w[2],那么当前状态cw[2][4]等于当前集装箱的重量w[2]加上上一阶段剩余容量为j-w[2]时的状态cw[2-1][4-4],当前阶段的决策取决于状态值大的,由此推出状态转移方程:
当w[i]<j时, cw[i][j] = cw[i-1][j];
当w[i]>=j时, cw[i][j]=max{cw[i-1][j] , cw[i-1][j-w[i]]+w[i]}。
有了状态转移方程就可以一步步递推出每个阶段的所有决策和状态,问题的解就是剩余容量为10时最后阶段的状态cw[5][10]。

1 /**最优装载-动态规划
2 * @param n
3 * @param c1
4 * @param w
5 * T(n)=O(nc1),S(n)=O(nc1)
6 */
7 private static void optimalLoading(int n, int c1,int[] w){
8 //存储每个阶段所有状态值的表
9 int[][] cw = new int[n+1][c1+1];
10 //遍历每个集装箱
11 for (int i = 1; i <= n; i++) {
12 //遍历一船剩余容量的每个情况
13 for (int j = 1; j <= c1; j++) {
14 //如果当前集装箱重量大于剩余容量肯定不装
15 if (w[i]>j){
16 //当前集装箱不装的决策造成的状态等于上一阶段同情况下的状态
17 cw[i][j]=cw[i-1][j];
18 }else {//当前集装箱能装下就比较装和不装哪个决策的状态值大
19 cw[i][j]=Math.max(cw[i-1][j],cw[i-1][j-w[i]]+w[i]);
20 }
21 }
22 }
23 System.out.println(cw [n][c]);
24 }/*第一层循环遍历n个集装箱,第二层循环遍历1船容量c1的所有值T(n)=O(nc1),需要一个长度为nc1的二维数组辅助,S(n)=O(nc1)*/
【例6】0-1背包问题:给定 n 种物品和一背包。物品 i 的重量是wi,其价值为 vi,背包的容量为 c。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
实例:n = 5,c = 10,w =(3,1,4,5,3),v =(10,6,3,11,12)
用动态规划的思想把问题分成多个阶段,每个阶段的决策就是一个物品放不放入背包这两个选择,决策造成的状态就是当前背包内物品的价值,当前阶段的决策要依赖上一阶段的状态,除此之外当前物品能不能装入背包还要考虑背包的剩余容量(客观条件)。为了方便后面阶段的决策,在当前阶段要对背包剩余容量的每个情况分别做出决策获得多个状态并存储到数组,下一阶段做决策时可以先把当前的物品装入背包,剩余的容量无论是多少都可以从数组中调用前面阶段的装入情况。
先设两个一维数组存储每个物品的重量和价值:int[] w = {0,3, 1, 4, 5, 3} ; int[] v = {0,10, 6, 3, 11, 12};然后设一个二维数组记录每个阶段的所有状态:int[][] cv = new int[n+1][c+1];如图把二维数组cv以表格形式表示,i和j是数组下标,i表示物品编号,j表示背包剩余容量,一维数组w和v放在左边方便参考对应物品的重量和价值。cv[i][j]表示第i个物品在背包剩余容量为j时做出的决策造成的状态。
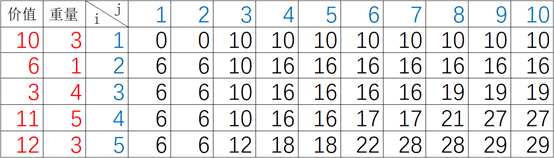
cv[2][4]表示背包剩余容量j=4时第2个物品的状态,如果装不下或者选择不装,cv[2][4]等于上一阶段j=4时的状态 cv[2-1][4],如果选择装下的话留给前面阶段的背包剩余容量为4-w[2],cv[2][4]等于当前物品的价值v[2]加上前面阶段能装下的物品的价值:cv[2-1][ 4-w[2]] ,由此得出状态转移方程:
w[i]>j时:cv[i][j] = cv[i-1][j];
w[i]<=j时:cv[i][j] max{ cv[i-1][ j], cv[i-1][ j-w[i]] + v[i]};

1 /**0/1背包问题-动态规划
2 * @param n 物品数
3 * @param c 背包容量
4 * @param w 物品重量
5 * @param v 物品价值
6 * T(n)=O(nc),S(n)=O(nc)
7 */
8 private static void optimalLoading(int n,int c,int[] w,int[]v){
9 //存储每个阶段所有状态值的表
10 int[][] cv = new int[n+1][c +1];
11 //遍历每个物品
12 for (int i = 1; i <= n; i++) {
13 //遍历背包剩余容量的每个情况
14 for (int j = 1; j <= c; j++) {
15 //如果当前物品重量大于剩余容量肯定不装
16 if (w[i]>j){
17 //当前物品不装的决策造成的状态等于上一阶段同情况下的状态
18 cv[i][j]= cv[i-1][j];
19 }else {//当前物品能装下就比较装和不装哪个决策的状态值大
20 cv[i][j]=Math.max(cv[i-1][j], cv[i-1][j-w[i]]+v[i]);
21 }
22 }
23 }
24 System.out.println(cw [n][c]);
25 }/*第一层循环遍历n个物品,第二层循环遍历c的所有值,T(n)=O(nc),需要一个长度为nc的二维数组辅助,S(n)=O(nc)*/
【例7】双重0-1背包问题:给定 n 种物品和一背包。物品 i 的重量是weighti,体积是volumei,其价值为 valuei,背包的容量为 c,容积为v。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
实例:n = 5,c = 5,v = 5,weight =(3,1,4,5,2),volume =(2,4,1,3,5),value = (10,6,3,11,12)
这题比上面那题多了一个限制条件,每个物品能不能装入背包除了要考虑背包容量还要考虑背包容积,为了方便后面阶段的决策,在当前阶段要对背包剩余容量的每个情况分别做出决策获得多个状态并存储到数组,下一阶段做决策时可以先把当前的物品装入背包,剩余的容量无论是多少都可以从数组中调用前面阶段的装入情况。
先设三个一维数组存储每个物品的重量体积和价值:int[] weight = {0,3, 1, 4, 5, 2}; int[] volume = {0,2, 4, 1, 3, 5}; int[] value = {0,10, 6, 3, 11, 12}; 再设一个三维数组存储每个状态值:int [][][] cv = new int[n+1][c+1][v +1]; 如图分别画出表示每个阶段所有状态的表格cv[i],第一行是备注当前物品的编号重量体积和价值,j表示当前背包剩余容量,k表示当前背包剩余容积,cv[i][j][k]表示第i件物品在背包剩余容量为j,剩余容积为k时的决策造成的当前背包内物品总价值(状态)。

对于当前阶段的物品如果选择不装,当前状态cv[i][j][k]等于上一阶段同情况下的状态cv[i-1][j][k],如果选择装入,留给上一阶段的容量为j- weight[i],容积为k- volume[i],当前状态cv[i][j][k]等于当前物品价值value[i]加上上一阶段容量为j- weight[i],容积为k- volume[i]时的状态cv[i - 1][j - weight[i]][k - volume[i]],哪个状态值大选哪个,由此得出每个阶段的状态转移方程:
当weight[i]>j, volume[i]>k时:cv[i][j][k]= cv[i-1][j][k],
当weight[i]<=j, volume[i]<=k时:
cv[i][j][k] = max(cv[i - 1][j][k], cv[i - 1][j - weight[i]][k - volume[i]] + value[i])。

1 /**双重0/1背包问题
2 * @param n 物品个数
3 * @param c 背包容量
4 * @param v 背包容积
5 * @param weight 物品重量
6 * @param volume 物品体积
7 * @param value 物品价值
8 * T(n)=O(ncv),S(n)=O(ncv)
9 */
10 private static void optimalLoading(int n, int c, int v, int[] weight, int[] volume, int[] value) {
11 //创建一个三维数组记录
12 int [][][] cv = new int[n+1][c+1][v +1];
13 //遍历物品
14 for (int i = 1; i <=n ; i++) {
15 //背包容量
16 for (int j = 1; j <=c ; j++) {
17 //背包体积
18 for (int k = 1; k <= v; k++) {
19 //当前物品i的重量比背包容量j大或体积比背包容积k大
20 if (weight[i] > j || volume[i] > k) {
21 cv[i][j][k] = cv[i - 1][j][k];
22 } else {//装得下,Max{装物品i, 不装物品i}
23 cv[i][j][k] = Math.max(cv[i - 1][j][k],
24 cv[i - 1][j - weight[i]][k - volume[i]] + value[i]);
25 }
26 }
27 }
28 }
29 System.out.println(cv[n][c][v]);
30 }/*第一层循环遍历n个物品,第二层循环遍历c的所有值,第三层循环遍历v的所有值,T(n)=O(ncv),需要一个长度为ncv的三维数组辅助,S(n)=O(ncv)*/
【例8】如下图是一个数塔,从顶部出发在每一个节点可以选择向左或者向右走,一直走到底层,要求找出一条路径,使得路径上的数字之和最大。

如果自顶向下算要用贪心算法,显然每步的最优决策不一定能得出全局的最优决策。如果用动态规划算法自底向上计算。先对倒数第一层的每个结点分别算出两个选择的值再对比得出最优值并记录以便上一层的结点调用,然后层数减一再重复这个过程就可以一步步递推得出全局最优值。
先把数塔存储到一个数组int[][] data = new int[5][5]:
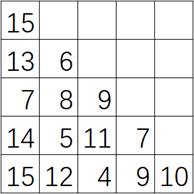
再设一个数组记录每一步决策的状态(最优值)int[][] dp = new int[5][5];
先把data最后一层的数据复制到dp,例如第四层第一个结点的决策为:
dp[3][0] = data[3][0]+ max(dp[4][0],dp[4][1])
故由此推出状态转移方程为:
dp[i][j] = data[i][j] + max(dp[i+1][j],dp[i+1][j+1]);
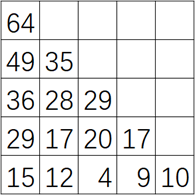
算出最优值再算最优解,另设一数组记录最优解:
int[] route = new int[5];
先记录第一个值
route[0]=data[0][0];
设一变量记录当前结点在当前层的位置
int j = 1;
循环遍历i
if(dp[i][j] < dp[i][j+1])j++; route[i]=j;
记录每一步的选择的节点
route[i]=data[i][j]

1 public static void main(String[] args) {
2 //数塔
3 int[][] data = {
4 {15, 0, 0, 0, 0},
5 {13, 6, 0, 0, 0},
6 { 7, 8, 9, 0, 0},
7 {14, 5,11, 7, 0},
8 {15,12, 4, 9,10}
9 };
10 pyramidOfNumber(data);
11 }
12 /**计算数塔最大值路径
13 * @param data 数塔数据
14 * T(n)=O(n^2),S(n)=O(n^2)
15 */
16 private static void pyramidOfNumber(int[][]data){
17 //数塔层数
18 int n = data.length;
19 //记录每一步的状态
20 int[][] dp = new int[n][n];
21 //先输入最后一层的数据
22 System.arraycopy(data[n - 1], 0, dp[n - 1], 0, n);
23 //自底向上遍历数塔,由下一层的数据计算上一层的数据
24 for (int i = n-2; i >=0; i--) {
25 for (int j = 0; j <= i; j++) {
26 //计算每一步的状态
27 dp[i][j] = data[i][j]+Math.max(dp[i+1][j],dp[i+1][j+1]);
28 }
29 }
30 //记录每一层选择的结点
31 int[] route = new int[n];
32 //记录第一个结点值
33 route[0]=data[0][0];
34 //j为当前结点在本层的位置
35 int j = 1;
36 for (int i = 0; i < n; i++) {
37 //如果右结点大就往右一格,否则和原来一样。
38 if (dp[i][j] < dp[i][j + 1]) {
39 j ++;
40 }
41 route[i] = data[i][j];
42 }
43 System.out.println("最优值为:"+dp[0][0]);
44 System.out.println("最优解为:"+Arrays.toString(route));
45 }
i=j 时:m[i][j]= 0;
i<j 时:m[i][j]= min{m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1]}(i<=k<j);
