事件概率期望方差基础知识

事件

1.集合的运算法则一般都可以
2.事件的互斥： $A\cap B=\phi$
3.事件的对立： $\bar A=B$
4.事件的和（并）： $A+B$ 或 $A\cup B$
5.事件的积（交）： $AB$ 或 $A\cap B$
6.事件的差（ $A$ 发生 $B$ 不发生）： $A-B=A\bar B$
7.事件的运算定律：交换律，结合律，分配律
8. $A+A=A,AA=A$
$(A-B)+B=A+B$
9.事件的独立性：
对于事件 $A,B$ 当 $P(AB)=P(A)*P(B)$ 称 $A,B$ 独立
事件独立和事件互斥理解：相互独立事件之间的发生互不影响,但可能会同时发生。 互斥事件是不可能同时发生的事件,即交集为零,但可能会产生相互影响。
10.相互独立和两两独立

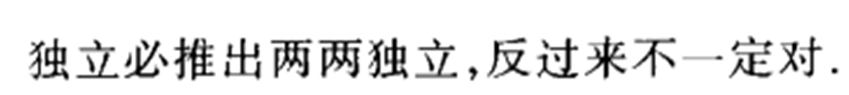
相互独立指的是 $A_i$ 与其他事件任意组合都独立，两两独立知时 $A_i$ 和 $A_j$ 独立

概率

1.类型：
$\quad$a. 古典概型： $P(X)=\frac{M}{N}$ ，有 $N$ 种等可能结果，事件在 $M$ 种结果中出现
$\quad$b.几何概型：每个事件发生的概率只与构成该事件区域的长度(面积或体积或度数)成比例： $P(X)=\frac{A}{S}$
2.概率加法定理：
3.条件概率：在 $B$ 事件发生的情况下， $A$ 事件发生的概率

$P(A|B)=\frac{P(AB)}{P(B)}$

推广： $P(AB)=P(A|B)*P(B)$
4.概率乘法定理：
两独立事件 $A,B$ 满足 $P(AB)=P(A)*P(B)$

5.全概率公式：

当 $B_1+B_2+...+B_n=\Omega，B_iB_j=\phi (i\not=j)$ ，

$P(A)=\sum_{i=1}^nP(AB_i)=\sum_{i=1}^nP(A|B_i)*P(B_i)$

6.叶贝斯公式：

当 $B_1+B_2+...+B_n=\Omega，B_iB_j=\phi (i\not=j)$ ，对于任一事件 $A$ 有：
$P(B_i|A)=\frac{P(A|B_i)*P(B_i)}{\sum_{i=j}^nP(A|B_j)*P(B_j)}$

期望

1.定义： $E(X)=i*P(X=i)$
2. 期望的线性性： $E(X+Y)=E(X)+E(Y)$
证明：
注意这里并没有要求 $X,Y$ 互斥
有更一般形式：
$E(\sum a_ix_i+b)=\sum a_iE(x_i)+b$
3. $X,Y$ 独立是 $E(XY)=E(X)*E(Y)$ 的充要条件
推导：
$E(XY)=\sum_x\sum_y xyP(X=x,Y=y)$
$\because XY=\phi$
$\therefore E(XY)=\sum_xxP(X=x)\sum yP(Y=y)=E(x)*E(y)$
4. $E(c)=c,E(E(X))=E(X)$ (因为此时 $E(X)$ 已经是确定的值)

方差

1. 本质：一种特殊的期望
2. 定义： $D(X)=E((X-E(X))^2)$
3. $D(X)=E((X-E(X))^2)=E(X^2-2*X*E(X)+E^2(X))=E(X^2)-E^2(x)$
   对于一些数的方差只是其一种特殊情况
4. $D(cX)=E((cX)^2)-E^2(cX)=c^2(E(X^2)-E^2(X))=c^2D(X)$
5. $D(X+c)=E((X+c-E(X+c))^2)=D(X)$

就先写到这里吧，差不多了…